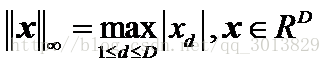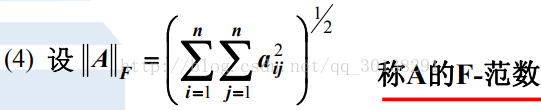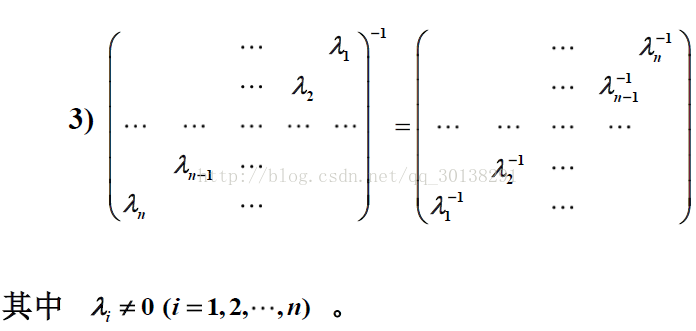转自:https://blog.csdn.net/qq_30138291/article/details/76327051
老师课堂总结,请勿转载
Numpy中的核心线性代数工具
numpy.linalg模块包含线性代数的函数。使用这个模块,我们可以计算逆矩阵、求特征值、解线性方程组以及求解行列式等。
求解矩阵的范数
在实数域中,数的大小和两个数之间的距离是通过绝对值来度量 的。在解析几何中,向量的大小和两个向量之差的大小是 “长度 ” 和 “ 距 离 ”的概念来度量的。为了对矩阵运算进行数值分析,我们需要对向量 和矩阵的 “大小 ”引进某种度量。范数是绝对值概念的自然推广。
"范数 "是对向量和矩阵的一种度量,实际上是二维和三维 向量长度概念的一种推广.
向量范数
范数理论的一个小推论告诉我们:ℓ1≥ℓ2≥ℓ∞
矩阵的范数
范数汇总
转载地址http://blog.csdn.net/u011361880/article/details/73527229
矩阵行列式
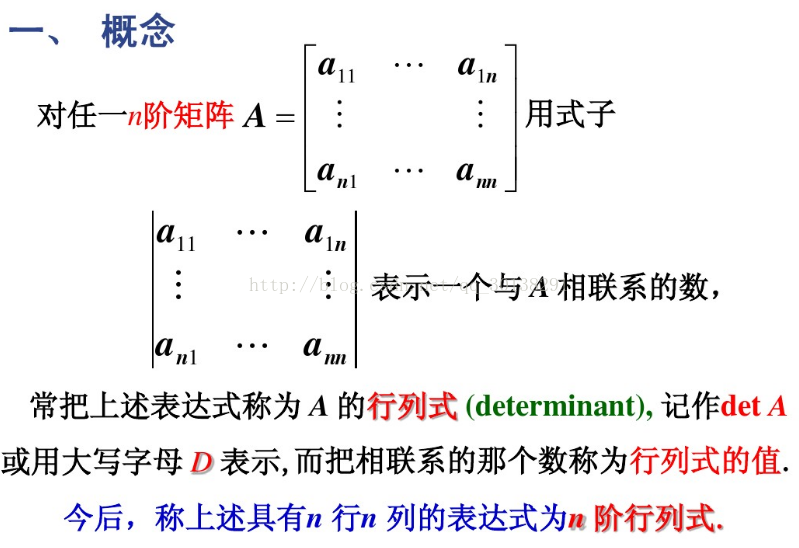
方阵的逆矩阵
伴随矩阵
逆矩阵运算性质
代码
-
# -*- coding: utf-8 -*-
-
"""
-
Created on Sat Jul 29 15:33:39 2017
-
-
@author: Administrator
-
"""
-
-
import numpy as np
-
-
print("###########向量范数#########")
-
print("向量为:",[1,5,6,3,-1])
-
print("1范数:",np.linalg.norm([1,5,6,3,-1],ord = 1),"向量元素绝对值之和")
-
print("2范数:",np.linalg.norm([1,5,6,3,-1],ord = 2),"向量元素绝对值的平方和再开方")
-
print("无穷范数:",np.linalg.norm([1,5,6,3,-1],ord = np.inf),"所有向量元素绝对值中的最大值")
-
-
print("###########矩阵范数#########")
-
a = np.arange(12).reshape(3,4)
-
print("矩阵a为:")
-
print(a)
-
print("F范数",np.linalg.norm(a,ord = 'fro'),"矩阵元素绝对值的平方和再开平方")
-
print("1范数",np.linalg.norm(a,ord = 1),"列和范数,即所有矩阵列向量绝对值之和的最大值")
-
print("2范数",np.linalg.norm(a,ord = 2),"谱范数,即ATA矩阵的最大特征值的开平方")
-
print("无穷范数",np.linalg.norm(a,ord = np.inf),"行和范数,即所有矩阵行向量绝对值之和的最大值")
-
-
-
print("###########行列式#########")
-
a = np.arange(1,17).reshape(4,-1)
-
print("矩阵a为")
-
print(a)
-
print("a的行列式为:",np.linalg.det(a))
-
-
print("###########逆矩阵np.linalg.inv()#########")
-
a = np.array([[1,-1],[1,1]])
-
b = np.array([[1/2,1/2],[-1/2,1/2]])
-
print("矩阵相乘为单位矩阵E:")
-
print(np.dot(a,b))
-
-
print("###########伴随矩阵#########")
-
print(a)
-
det_a = np.linalg.det(a)
-
print("a的行列式为:",det_a)
-
inv_a = np.linalg.inv(a)####求a的逆矩阵
-
print("a的逆矩阵为:",inv_a)
-
print("a的伴随矩阵为:")
-
bansui = det_a*inv_a
-
print(bansui)
-
print("验证:",np.dot(bansui,a))
-
-
print("###########A与A逆行列式#########")
-
a = np.random.rand(5,5)
-
inv_a = np.linalg.inv(a)
-
det_a = np.linalg.det(a)
-
det_inv_a = np.linalg.det(inv_a)
-
print(det_a*det_inv_a)
-
-
print("###########矩阵的幂matrix_power()#########")
-
a = np.random.rand(3,3)
-
print(a)
-
print(np.linalg.matrix_power(a,2))
-
-
print("###########求解AXB=C?#########")
-
a = np.array([[1,2,3],[2,2,1],[3,4,3]])
-
b = np.array([[2,1],[5,3]])
-
c = np.array([[1,3],[2,0],[3,1]])
-
det_a = np.linalg.det(a)
-
det_b = np.linalg.det(b)
-
inv_a = np.linalg.inv(a)
-
inv_b = np.linalg.inv(b)
-
if det_a != 0:
-
if det_b !=0:
-
x = np.dot(np.dot(inv_a,c),inv_b)
-
print(x)
-
###########向量范数#########
-
向量为: [1, 5, 6, 3, -1]
-
1范数: 16.0 向量元素绝对值之和
-
2范数: 8.48528137424 向量元素绝对值的平方和再开方
-
无穷范数: 6.0 所有向量元素绝对值中的最大值
-
###########矩阵范数#########
-
矩阵a为:
-
[[ 0 1 2 3]
-
[ 4 5 6 7]
-
[ 8 9 10 11]]
-
F范数 22.4944437584 矩阵元素绝对值的平方和再开平方
-
1范数 21.0 列和范数,即所有矩阵列向量绝对值之和的最大值
-
2范数 22.4092981633 谱范数,即ATA矩阵的最大特征值的开平方
-
无穷范数 38.0 行和范数,即所有矩阵行向量绝对值之和的最大值
-
###########行列式#########
-
矩阵a为
-
[[ 1 2 3 4]
-
[ 5 6 7 8]
-
[ 9 10 11 12]
-
[13 14 15 16]]
-
a的行列式为: 4.73316543133e-30
-
###########逆矩阵np.linalg.inv()#########
-
矩阵相乘为单位矩阵E:
-
[[ 1. 0.]
-
[ 0. 1.]]
-
###########伴随矩阵#########
-
[[ 1 -1]
-
[ 1 1]]
-
a的行列式为: 2.0
-
a的逆矩阵为: [[ 0.5 0.5]
-
[-0.5 0.5]]
-
a的伴随矩阵为:
-
[[ 1. 1.]
-
[-1. 1.]]
-
验证: [[ 2. 0.]
-
[ 0. 2.]]
-
###########A与A逆行列式#########
-
1.0
-
###########矩阵的幂matrix_power()#########
-
[[ 0.66673632 0.24542188 0.24331174]
-
[ 0.81223569 0.41511886 0.20157493]
-
[ 0.07107783 0.64497704 0.29675985]]
-
[[ 0.66117181 0.42244142 0.28390083]
-
[ 0.89304891 0.50167529 0.34112338]
-
[ 0.59235659 0.47658948 0.23537168]]
-
###########求解AXB=C?#########
-
[[ -2. 1.]
-
[ 10. -4.]
-
[-10. 4.]]