决策树(初识)

决策树:

• • 决策树方法在分类,预测,规则等领域有这广泛的应用,20世纪70年代后期和80年代初期,机器学习研究者提出了ID3算法后,决策树在机器学习,数据挖掘领域取得极大的发展,后来又有了c4.5,成为新的监督学习算法.1984年,几位科学家提出了CART分类算法,ID3和CART算法同时被提出,但都是采用类似的方法训练样本中学习决策树
  • 决策树是一种树状结构,它的每一个叶节点对应着一个分类,非叶子节点对应着在某个属性上的划分,根据样本在该属性上的不同取值将其划分成若干个子集.对于非纯的叶子节点,多数类的标号给出到达这个节点的样本所属的类,构造决策树的核心问题是在每一步如何选择适当的属性对样本做拆分.对于一个分类问题,从已知类标记的训练样本中学习并构造出决策树是一个自上而下,分而治之的过程.

  • 决策树算法	算法 描述
    C4.5算法	C4.5决策树生成算法相当于ID3算法的重要改进是使用信息增益率来选择节点属性.C4.5算法可疑克服ID3算法存在的不足:ID3算法只适用于离散的描述属性,而C4.5算法即能够处理离散的描述性,也可以处理连续的描述属性
    CART算法	CART决策树是一种十分有效的非参数分类和回归方法,通过构建树,修剪树,评估树来构建一个二叉树.当终结点是连续变量时,该树为回归树,当终结点是分类变量,该树为分类树
    ID3算法	其核心的是在决策树的各级节点上,使用信息增益方法作为属性的选择标准,来帮助确定生成每个节点是所应采用的合适属性

• ID3算法简介及基本原理

  • ID3算法基于信息熵来选择最佳测试属性.它选择当前样本集中具有最大信息增益值的属性作为测试属性;样本集的划分则依据测试属性的取值进行,测试属性有多少不同取值旧将样本集划分为多少子样本集,同时决策树上相应于该样本集的节点长出新的叶子节点.ID3算法根据信息论理论,采用划分后样本集的不确定性作为衡量划分好坏的标准,用信息增益值度量不确定性;信息增益值越大,不确定性越小.因此,ID3算法在每个非叶节点选择信息增益最大的属性作为测试属性,这样可疑得到当前情况下最纯的拆分,从而得到较小的决策树
  • 设S是s个数据样本的集合.假定类别属性具有m个不同的值:C_i(i=1,2,...,m),设si是类Ci中的样本数.对于一个给定的样本,它总是信息熵为
  • 
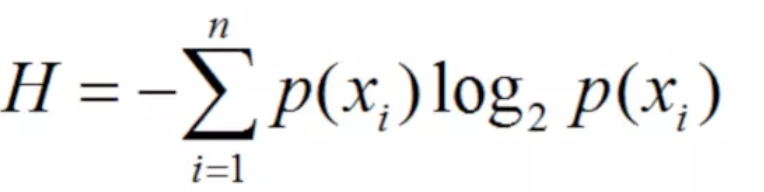
  • 其中,P_i是任意样本属于C_i的概率,一般可以用s_i/s估计
  • 设一个属性A具有k个不同的值{a₁,a₂,a₃...a₄},利用属性A将集合S划分为个子集{S₁,S₂,...S_k},其中S_j包含了集合S中属性A取a_j值的样本.若选择属性A为测试属性,则这些子集就是从集合S的节点生长出来的新的叶节点.设Sij是子集S_j中类别为Ci的样本数,则根据属性A划分样本的信息熵值为　
  • • • E(A) = ∑^k_j=1(s1j+ s2j + ... + smj)/I(sj,s2j,...smj)
      • 其中,I(s1j, s2j,...smj) = -∑^m_i=1P_ijlog₂(Pij), Pij = s_ij/(s_1j + s_2j + ...s_mj)是子集S_j只能给类别为C_i的样本的概率
      • 最后,用属性A划分样本集S后所得到的信息增益(Gain)为
        • Gain(A) = I(s₁, s₂, ..., s_m) - E(A)
      • 显然E(A)越小,Gain(A)的值越大,说明选择测试属性A对于分类提供的信息越大,选择A之后对分类的分类提供的信息越大,选择A之后对分类的不确定成都越小.属性A的K个不同的值对应样本集S的k个子集或分支,通过递归调用上述的过程(不包括已经选择的属性),生成其他属性作为节点和分支来生成整个决策树.ID3决策树算法作为一个典型的决策树学习算法,其核心是在决策树的各级节点上都用信息增益作为判断标准进行属性的选择,使得在每个非叶节点上进行测试时,都能获得最大的类别分别增益,使分类后的数据集的熵最小,这样的处理方法,使得树的平均深度较小,从而有效提高了分类效益..
    • ID3算法的具体流程:
      1. 对当前样本集合,计算所有属性的信息增益;
      2. 选择信息增益最大的属性作为测试属性,把测试数属性取值相同的样本划分为同一个子集样本集
      3. 若子样本集的类别属性止汗有单个属性,则分支为叶子节点,判断其属性值并标上相应的符号,然后返回调用出;否则对子样本集递归调用本算法
    • 下面对餐饮公司的例子进行那个剖析,一下是处理后的数据:
• 　

  序号,天气,是否周末,是否促销,销量
  1,坏,是,是,高
  2,坏,是,是,高
  3,坏,是,是,高
  4,坏,否,是,高
  5,坏,否,是,高
  6,好,否,否,低
  7,好,是,否,低
  8,好,是,是,高
  9,好,是,是,高
  10,好,否,是,高
  11,坏,是,是,低
  12,坏,是,否,低
  13,坏,否,否,低
  14,好,是,是,高
  15,好,是,是,高
  16,好,否,是,高
  17,好,否,是,高
  18,坏,否,是,低
  19,坏,否,是,低
  20,坏,是,否,低
  21,坏,是,否,低
  22,好,是,是,高
  23,好,否,是,高
  24,好,否,是,高
  25,好,否,否,低
  26,坏,否,否,低
  27,坏,是,否,低
  28,坏,是,是,高
  29,好,是,是,高
  30,好,否,否,低
  31,好,否,是,低
  32,坏,是,是,高
  33,坏,是,是,低
  34,坏,是,是,低

  • • 采用ID3算法构建决策树模型的具体步骤如下:
      1. 根据上边的信息熵公式,计算总的信息熵,其中数据中国总的记录数为34,而销售数量为"高"的数据有18,"低"的有16.
         1. I(18,16) = -18/34log₂18/34 - 16/34log₂16/34 = 0.997503
      2. 根据总的总的信息熵公式和划分样本的信息熵公式,来计算每个测试属性的信息熵,对于天气属性,其属性值有"好"和"坏"两种,其中天气为"好"的条件下,销售数量为高的记录为11,销售数量为低的记录为6天剋表示为(11,6),天气为"坏"的条件下,销售数量为"高"的记录为7天,销售数量为"低"的记录为10可表示为(7,10),则天气属性的信息熵计算过程如下.
         1. I(11,6) = -11/17log₂11/17 - 6/17log₂6/17 = 0.936667
         2. I(7,10) = -7/17log₂7/17 - 10/17log₂10/17 = 0.977418
         3. E(天气) = 17/34I(11,6) + 17/24(7,10) = 0.957034
      3. 对于是否周末属性,其属性值有"是"和"否"两种,其中是否周末属性为"是"的条件下,起销售数量为"高"的记录为11,销售数量为低的记录为3,可表示为(11,3),是否周末属性为"否"的条件下,销售数量为"高"的记录为7,而销售数量为"低"的记录为13可表示为(7,13),则节假日属性的信息熵计算过程如下:
         1. I(11,3) = -11/14log₂11/14 - 3/14log₂3/14 = 0.749595
         2. I(7,13) = -7/20log₂7/20 - 13/20log₂13/20 = 0.934068
         3. E(是否周末) = -14/34I(11,3) + 20/34I(7,13) = 0.858109
      4. 对于是否有促销属性,其属性值有"是"和"否"两种.其中,是否有促销属性为"是"的条件下,销售数量为"高"的记录为15,销量为"低"的记录视为7,可表示为(15,7);其中是否有促销属性为"否"的条件下.销售数量为"高"的记录为3,销售数量为"低"的金鸡路为9,可表示为(3,9).则是否有促销属性的信息熵计算过程如下:
         1. I(15,7) = -15/22log₂15/22 - 7/22log₂7/22 = 0.902393
         2. I(3,9) = -3/12log₂3/12 - 9/12log₂9/12 = 0.811278
         3. E(是否有促销) = -22/34I(15,7) + 12/34I(3,9) = 0.870235
      5. 根据公式,计算天气,是否周末和是否有促销属性的信息增益值
         1. Gain(天气) = I(18, 16) - E(天气) = 0.997503 - 0.957043 = 0.04046
         2. Gain(是否周末) = I(18, 16) - E(是否周末) = 0.997503 - 0.858109 = 0.139394
         3. Gain(是否有促销) = I(18, 16) = E(是否促销) = 0.997503 - 0.870235
      6. 由上边的计算结果可以知道,是否周末属性的信息增益值最大,它的两个属性值"是"和"否"作为该根结点的两个分支,然后按照1-5的步骤进行节点的划分,针对每一个分支节点继续进行信息增益的计算,如此反复循环,直到没有新的结点分支,最终构成一颗决策树
    • 由于ID3决策树算法采用了信息增益作为选择测试属性的标准,会偏向于选择取值较多的,即所谓高度分支属性,而这类属性并不一定是最优的属性.同时ID3决策树算法只能处理离散属性,对于连续性的属性,在分类前需要对其进行离散化,为了解决倾向于选择高度分支属性的问题,人们采用信息增益率作为选择测试属性的标准,这样便得到C4.5决策树算法.此外,常用的决策树算法还有CART算法,SLIQ算法,SPRINT算法和PUBLIC算法等.

  • # -*- coding:utf-8 -*-
    
    import sys
    
    reload(sys)
    sys.setdefaultencoding("utf-8")
    
    """
    利用ID3决策树算法预测销量高低
    """
    
    # 参数初始化
    import pandas as pd
    data = pd.read_csv("./practice_data.csv", header=None, sep=",",
                       names=["number", "tianqi", "weekend", "pt", "count"])
    
    print data["tianqi"]
    # 数据是类别标签,要将她转换成数据
    # 用1来表示"好", "是", "高"这三个属性,用-1来表示"坏","否","低"
    data[data["tianqi"] == u"好"] = 1
    data[data["tianqi"] == u"坏"] = -1
    print data["tianqi"]
    data[data["weekend"] == u"是"] = 1
    data[data["weekend"] == u"否"] = -1
    print data["weekend"]
    data[data["pt"] == u"是"] = 1
    data[data["pt"] == u"否"] = -1
    data[data["count"] == u"高"] = 1
    data[data["count"] == u"低"] = -1
    print data
    
    
    # print data
    x = data.iloc[:,:3].as_matrix().astype(int)
    y = data.iloc[:,3].as_matrix().astype(int)
    
    from sklearn.tree import DecisionTreeClassifier as DTC
    dtc = DTC(criterion="entropy")  # 建立决策树模型, 基于信息熵
    dtc.fit(x, y)  # 训练模型
    
    # 导入相关函数,可视化决策树
    # 导出的结果是一个dot文件, 需要安装Graphviz才能将它转化为pdf或png等格式
    from sklearn.tree import export_graphviz
    from sklearn.externals.six import StringIO
    with open("tree.dot", "w") as f:
        f = export_graphviz(dtc, feature_names=x.columns, out_file=f)