from bayes_opt import BayesianOptimization
# 定义黑盒函数
def lgb_cv(n_estimators,learning_rate,max_depth,num_leaves,min_child_samples,subsample,colsample_bytree,reg_alpha,reg_lambda,min_child_weight):
val = cross_val_score(
LGBMClassifier(n_estimators=int(n_estimators),
random_state=2019,
learning_rate=learning_rate,
max_depth=int(max_depth),
num_leaves=int(num_leaves),
min_child_samples=int(min_child_samples),
subsample=min(subsample, 0.99999),
colsample_bytree=min(colsample_bytree, 0.9999),
reg_alpha=reg_alpha,
reg_lambda=reg_lambda,
min_child_weight=min_child_weight,
class_weight='balanced',
), train_x[use_col], train_y, scoring='roc_auc', cv=5,n_jobs=-1
).mean()
return val
# 给定超参数搜索空间
opt = BayesianOptimization(
lgb_cv,
{'n_estimators': (600, 1000),
'learning_rate':(0.005,0.015),
'max_depth':(2,5),
'num_leaves':(6,16),
'min_child_samples':(10,50),
'subsample':(0.6,0.99),
'colsample_bytree':(0.6,0.99),
'reg_alpha':(0.05,1),
'reg_lambda':(0.05,1),
'min_child_weight':(1,100)
}
)
opt.maximize() # 最大化黑盒函数
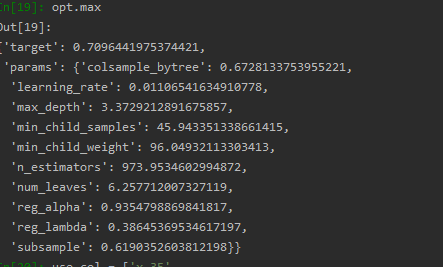
opt.max # 返回黑盒函数值最大的超参数
执行 opt.maximize()示意截图

执行opt.max 示意截图