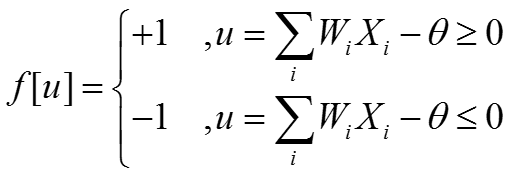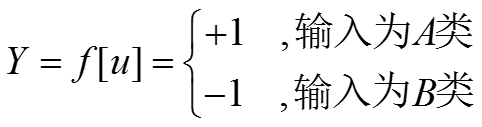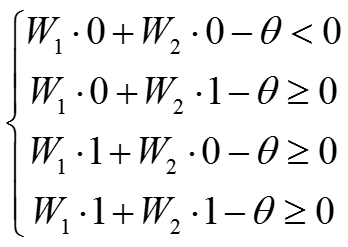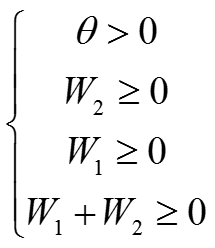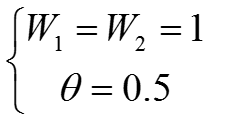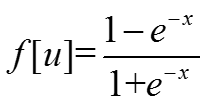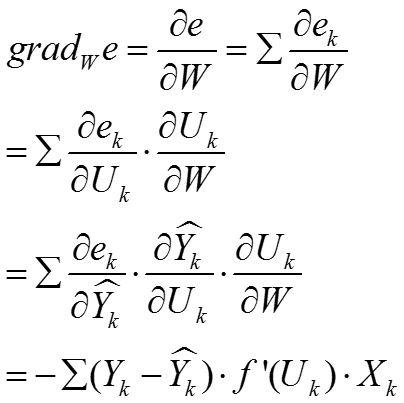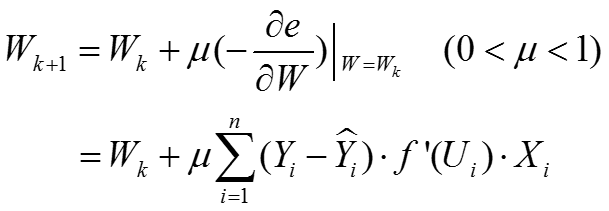神经网络(Neural Network)概述

1.神经网络概况

1943年，心理学家W.Mcculloch和数理逻辑学家W. Pitts根据生物神经元功能和结构，提出M-P神经元模型。

1957年，Rosenblatt提出感知机MLP模型。

Rosenblatt, Frank.x. Principles ofNeurodynamics:Perceptrons and the Theory of Brain Mechanisms. Spartan Books, Washington DC,1961.

1981年，Kohonen于1981年提出了自组织映射(SOM)网络。
T. Kohonen,Self-organizedformation of topologically correct feature maps, Biological Cybernetics.1982.43:59-69.

1982年，Hopfield提出Hopfield网络，用于联想记忆和优化。
John J. Hopfield, Neural networks andphysical systems with emergent collective computational abilities, Proc. Natl. Acad. Sci.USA, vol. 79 no. 8, pp. 2554–2558, April 1982.
1986年，Rumelhart和McCelland等提出了误差反向传播(BP)算法，用于多层前馈神经网络的优化。迄今为止应用最广的神经网络学习算法。
Rumelhart, David E.; Hinton,Geoffrey E.; Williams, Ronald J. (8 October 1986).Learningrepresentations byback-propagatingerrors.Nature 323 (6088): 533–536.
------------------------------------------------------------------------------------------------------------------

2.神经网络的学习机理

神经网络分为两种，一种叫做有导师学习，一种叫做无导师学习。有导师学习是感知器的学习规则；而无导师学习是认知器的学习规则。典型的有导师学习网络有BP网络，Hopfield网络；而典型的无导师学习网络有ART网络，Kohonen网络。所谓的“导师”，是指的“导师信号”，也就是学习过程中的监督信号，是在神经网络学习中由外部提供的模式样本信号。

1.)感知器的学习结构

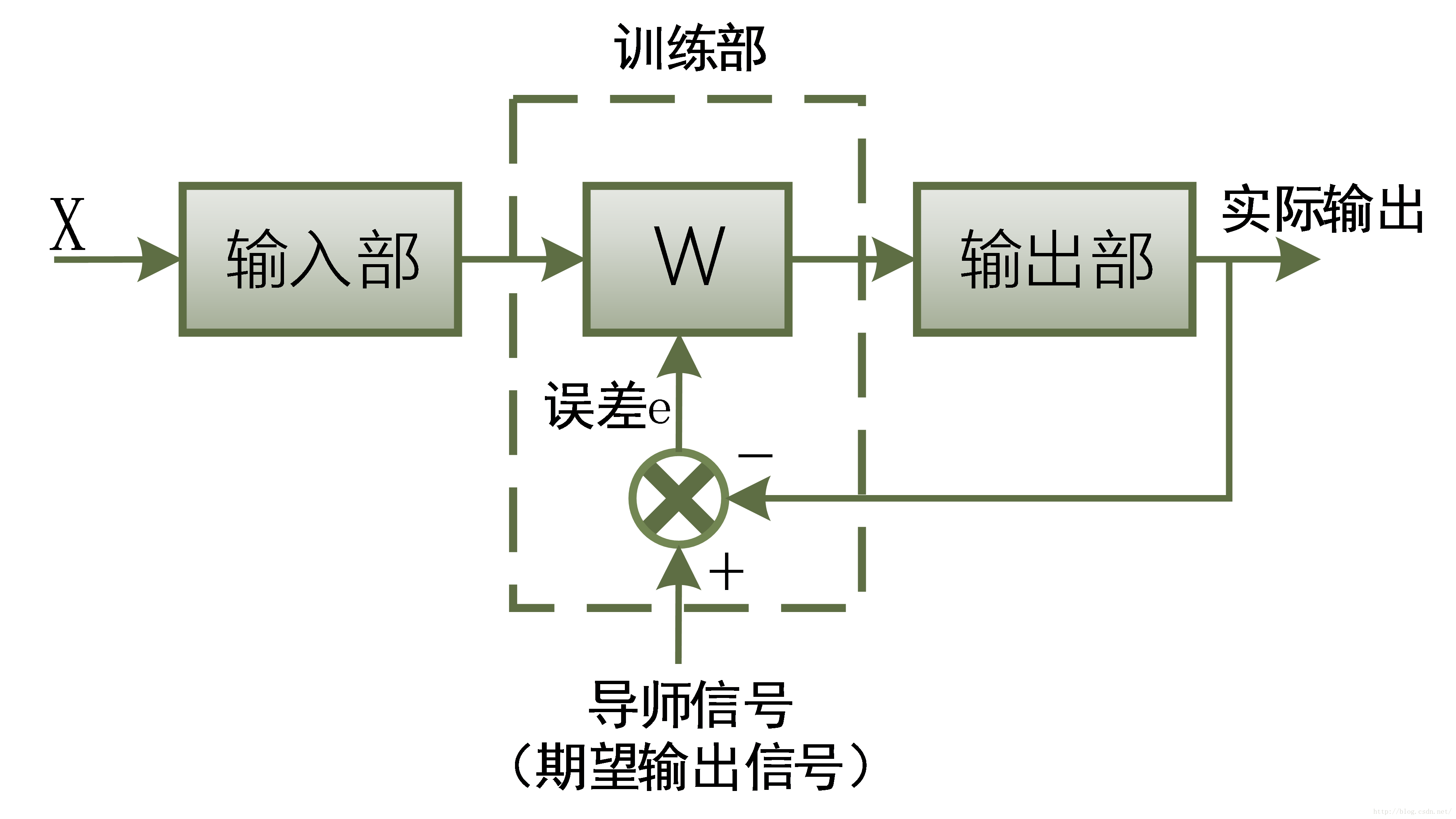
感知器的学习是神经网络最经典的学习。如下图所示，感知器的学习分为三个部分：输入部、训练部和输出部。某种模式样本X从输入部输入到感知器中，经过训练部的权值处理后，从输出部输出；而输出部的实际输出与导师信号(期望输出信号)做比较，产生误差信号e，这里反应了实际与期望(现实和理想)的差距；然后通过误差信号e调整训练部的权值W，使得新产生的W能让误差信号尽可能的小(实际与期望尽可能接近)，从而达到训练的作用。

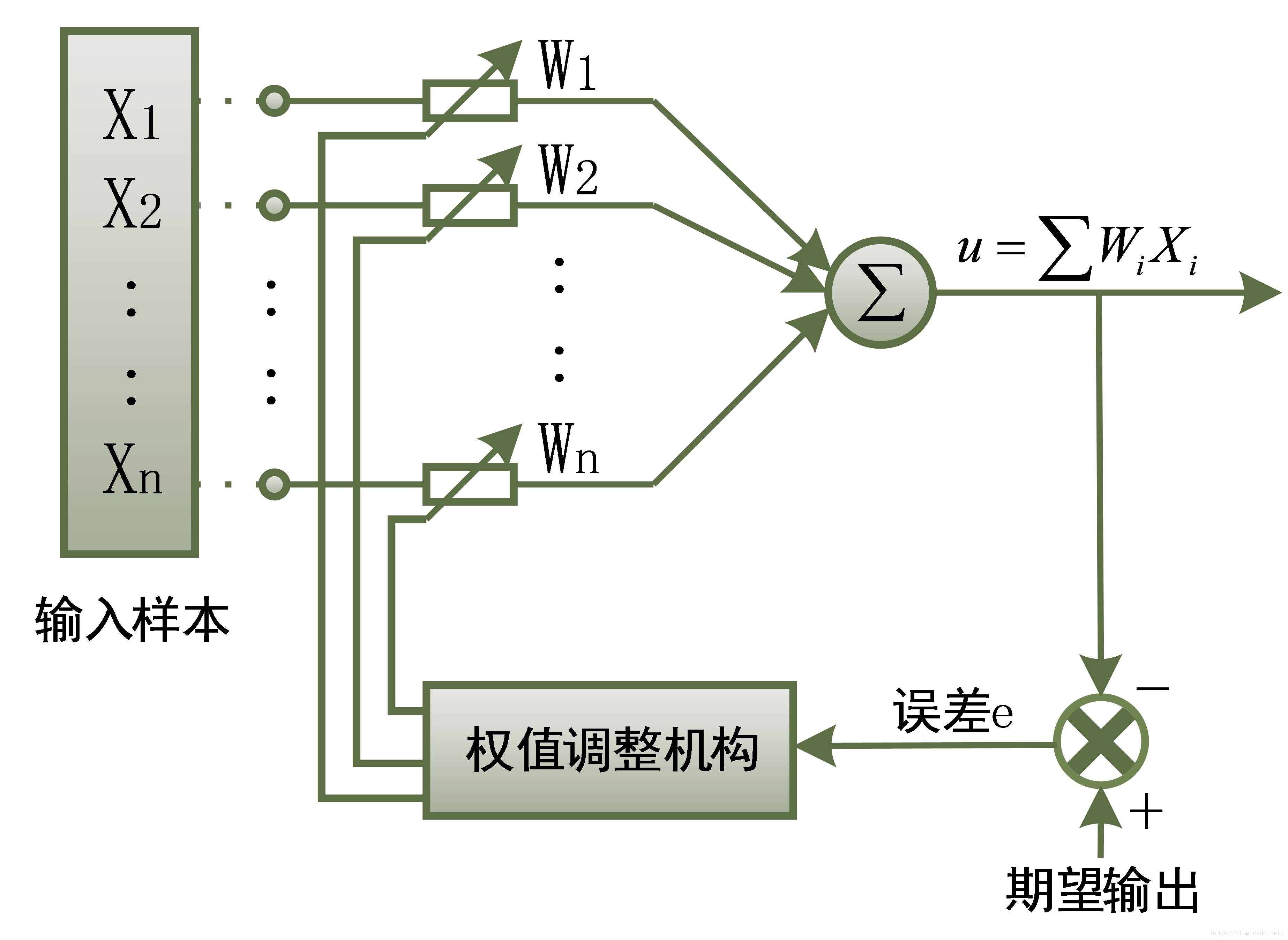
下图是神经网络中具体的结构图。输入样本X是一个n维向量，记为{X1,X2,...,Xn}，相应的权值也为一个n维向量，记为{W1,W2,...,Wn}。训练过程如上所述，X的n个元素与对应的n个权值分别相乘再求和，得到输出u，输出与期望输出相减得到误差信号e，误差通过权值调整机制修改相应的W权值，使得误差最小。这也预示着此种训练的判决条件是“最小误差准则”。

2.)感知器的学习算法

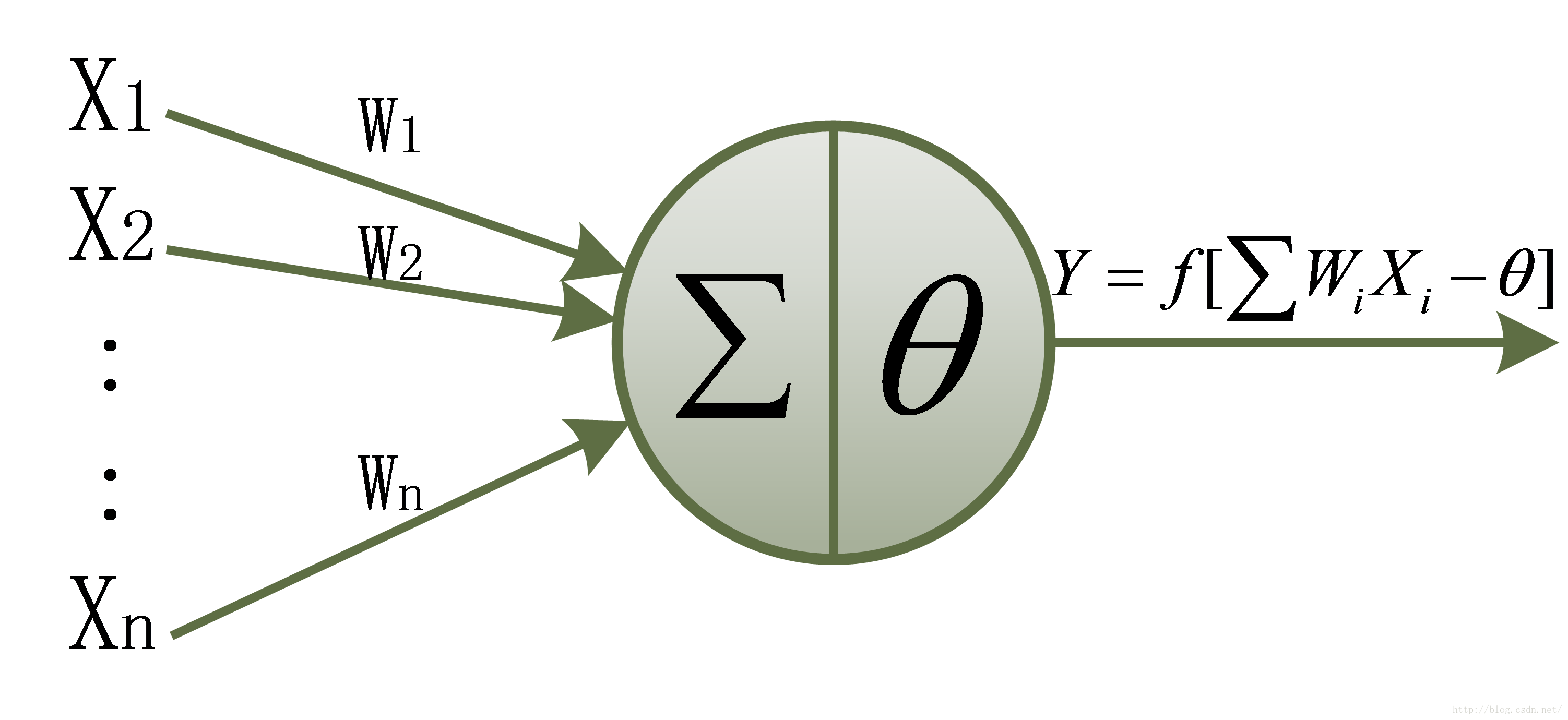
感知器是有单层计算单元的神经网络，由线性元件和阈值元件组成。如图，线性元件指的是输入向量与权值的加权求和操作，而阈值元件指的是得到的结果 u 要经过一个非线性处理 f 得到最终的输出Y。

所以感知器的数学模型为：

其中，基本的非线性函数为符号函数，取值为+1或-1：

感知器最大的作用就是对输入样本进行分类。所以感知器可以作为分类器，如定义：

上式中感知器的分类边界为：

如此，我们可以总结一下感知器的算法流程：

      (1)对权系数置初值 w = (W1,W2,...,Wn,Wn+1)；

      (2)输入样本 X = (X1,X2,...,Xn,Xn+1) 以及它的期望 d；

      (3)计算实际的输出值：

      (4)根据实际的输出求出误差：

      (5)用误差 e 去修改权值系数：

      (6)转到第(2)步，一直执行到一切样本都已稳定为止。

其中，在初始化时，有：

3.)感知器分类的例子

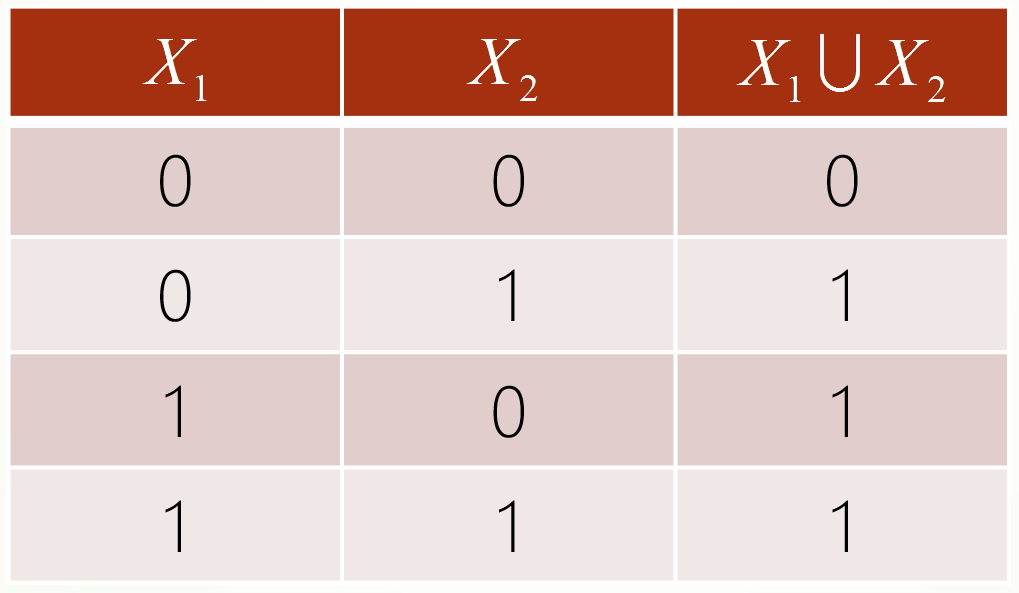
如图，我们有一张X1与X2的真值表：

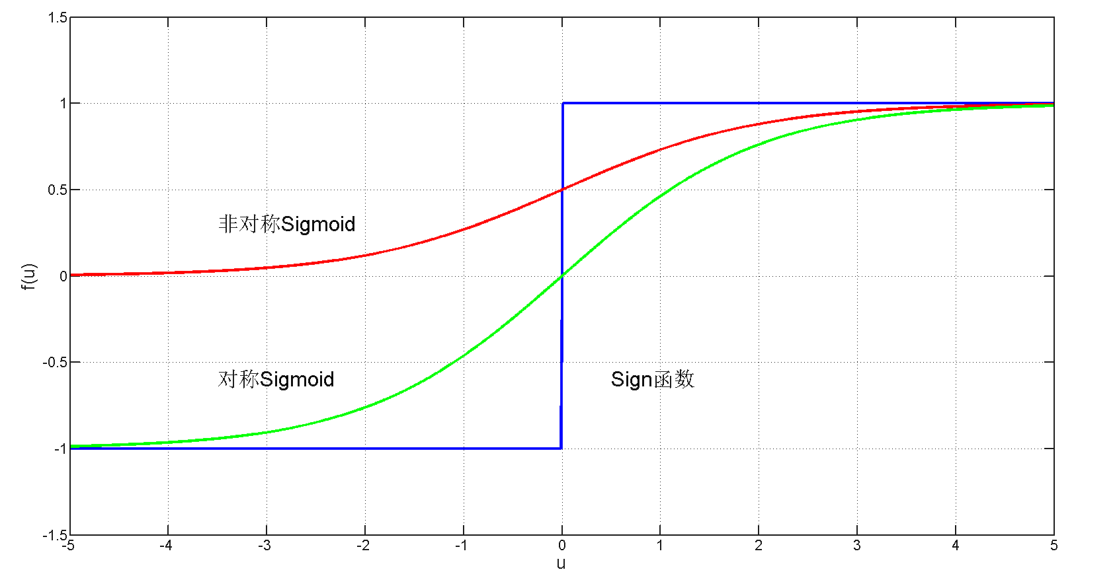
我们定义X1与X2的值为1的为A类，X1与X2的值为0的为B类。于是我们认为，输出向量X是一个2维向量{X1,X2}，而权值向量为{W1,W2}。我们根据感知器的传递函数，列出以下关系式：

解上述方程得到：

取值：

此时感知器的边界为：

分类结果如下图：

4.)神经网络学习的梯度算法

对于感知器的学习算法，因其传递函数（阶跃函数）的简单而存在局限性：

• 当函数不是线性可分时，则求不出结果；
• 不能推广到一般的前馈网络中。
  

为了克服存在的问题，所以人们提出了另一种算法：梯度算法(LMS法)

这种算法是在前面的算法上进行了三种改进：

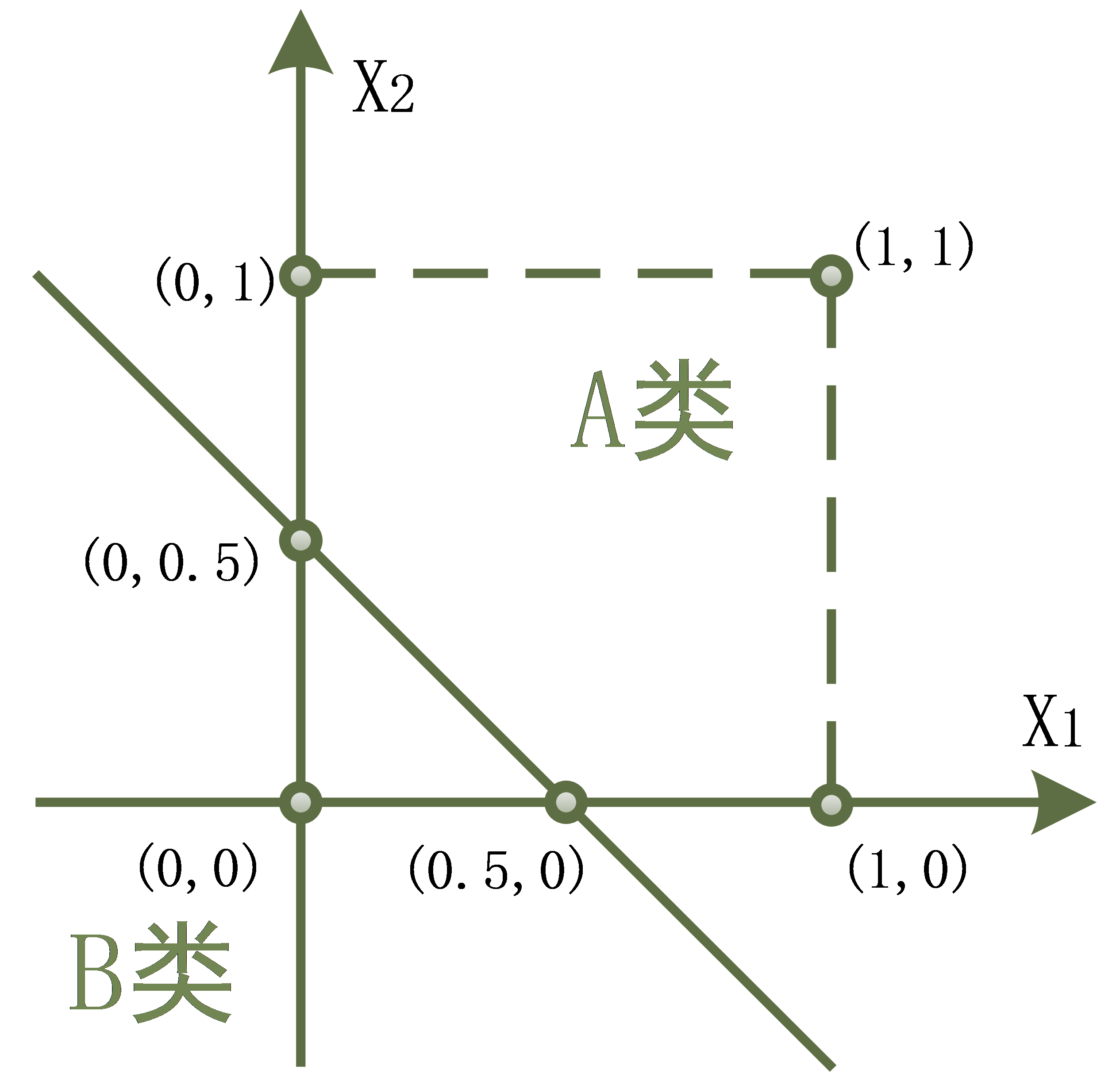
(1)改进一：将激励函数从阶跃函数改为了可微分的Sigmoid函数：

非对称型： 或 对称型：

(2)改进二：改变了误差公式的计算方法：

要使得误差 e 对权值系数 W 最小：

(3)改进三：按负梯度方向修改权值系数 W 。

算法流程方面与感知器的算法流程一致。

梯度法的优点在于：

• 神经元传递函数采用连续S型函数，而不是阶跃函数；
• 对权值系数的修改采用误差的梯度去控制，而不是采用误差去控制；
• 具有更好的动态特性，加快收敛进程。
  

------------------------------------------------------------------------------------------------------------------

总结

• 神经网络可以用于分类、聚类、预测等用途；
• 神经网络需要有一定量的历史数据，通过历史数据的训练，网络可以学习到数据中隐含的知识。
• 神经网络已被用来解决各种各样的很难用普通的以规则为基础的编程解决的任务，包括计算机视觉和语音识别。

如有任何疑问，欢迎一起讨论。

如要转载本文，请注明出处：http://blog.csdn.net/ws_20100/