贝叶斯思想以及与最大似然估计、最大后验估计的区别

ML-最大似然估计

MAP-最大后验估计

贝叶斯估计

三者的关系及区别

（本篇博客来自李文哲老师的微课，转载请标明出处http://www.cnblogs.com/little-YTMM/p/5399532.html ）

一。机器学习

　　核心思想是从past experience中学习出规则，从而对新的事物进行预测。对于监督学习来说，有用的样本数目越多，训练越准确。

用下图来表示机器学习的过程及包含的知识：

简单来说就是：

1. 首先要定义我们的假设空间（Model assumption）：如线性分类，线性回归，逻辑回归，SVM，深度学习网络等。
2. 如何衡量我们学出来的模型的好坏？定义损失函数（目标函数），lost function，如square loss
3. 如何对假设的模型做优化，及optimization过程。简单说，就是选择一种算法（如：梯度下降，牛顿法等），对目标函数进行优化，最终得到最优解；
   1. 不同的模型使用不同的算法，如逻辑回归通常用梯度下降法解决，神经网络用反向推导解决，贝叶斯模型则用MCMC来解决。
   2. 机器学习 = 模型 + 优化（不同算法）
4. 还有一个问题，模型的复杂度怎么衡量？因为复杂的模型容易出现过拟合（overfitting）。解决过拟合的方就是加入正则项（regularization）
5. 以上问题都解决之后，我们怎么判断这个解就是真的好的呢？用交叉验证（cross-validation）来验证一下。

二。ML vs MAP vs Bayesian

1. ML（最大似然估计）：就是给定一个模型的参数，然后试着最大化p(D|参数)。即给定参数的情况下，看到样本集的概率。目标是找到使前面概率最大的参数。
   1. 逻辑回归都是基于ML做的；
   2. 缺点：不会把我们的先验知识加入模型中。
2. MAP（最大后验估计）：最大化p(参数|D)。
3. Bayesian：我们的预测是考虑了所有可能的参数，即所有的参数空间（参数的分布）。

• ML和MAP都属于同一个范畴，称为（freqentist），最后的目标都是一样的：找到一个最优解，然后用最优解做预测。

     

三。ML

我们需要去最大化p(D|参数)，这部分优化我们通常可以用把导数设置为0的方式去得到。然而，ML估计不会把先验知识考虑进去，而且很容易造成过拟合现象。

举个例子，比如对癌症的估计，一个医生一天可能接到了100名患者，但最终被诊断出癌症的患者为5个人，在ML估计的模式下我们得到的得到癌症的概率为0.05。

这显然是不太切合实际的，因为我们根据已有的经验，我们知道这种概率会低很多。然而ML估计并没有把这种知识融入到模型里。

四。MAP

通过上面的推导我们可以发现，MAP与ML最大的不同在于p(参数)项，所以可以说MAP是正好可以解决ML缺乏先验知识的缺点，将先验知识加入后，优化损失函数。

其实p(参数)项正好起到了正则化的作用。如：如果假设p(参数)服从高斯分布，则相当于加了一个L2 norm；如果假设p(参数)服从拉普拉斯分布，则相当于加了一个L1 norm。

五。Bayesian

再次强调一下： ML和MAP只会给出一个最优的解， 然而贝叶斯模型会给出对参数的一个分布，比如对模型的参数, 假定参数空间里有参数1,参数2, 参数3,...参数N，贝叶斯模型学出来的就是这些参数的重要性（也就是分布），然后当我们对新的样本预测的时候，就会让所有的模型一起去预测，但每个模型会有自己的权重（权重就是学出来的分布）。最终的决策由所有的估计根据其权重做出决策。

模型的ensemble的却大的优点为它可以reduce variance, 这根投资很类似，比如我们投资多种不同类型的股票，总比投资某一个股票时的风险会低。

六。上面提到了frequentist和bayesian，两者之间的区别是什么？

 用一个简答的例子来再总结一下。 比如你是班里的班长，你有个问题想知道答案，你可以问所有的班里的学生。 一种方案是，问一个学习最好的同学。 另一种方案是，问所有的同学，然后把答案综合起来，但综合的时候，会按照每个同学的成绩好坏来做个权重。 第一种方案的思想类似于ML,MAP，第二种方案类似于贝叶斯模型。

七。Bayesian的难点

所以整个贝叶斯领域的核心技术就是要近似的计算 p( heta|D），我们称之为bayesian inference,说白了，这里的核心问题就是要近似这个复杂的积分（integral), 一种解决方案就是使用蒙特卡洛算法。比如我想计算一个公司所有员工的平均身高，这个时候最简答粗暴的方法就是让行政去一个一个去测量，然后计算平均值。但想计算所有中国人的平均身高，怎么做？（显然一个个测量是不可能的）

即采样。我们随机的选取一些人测量他们的身高，然后根据他们的身高来估计全国人民的审稿。当然采样的数目越多越准确，采样的数据越有代表性越准确。这就是蒙特卡洛算法的管家思想。

再例：

假设我们不知道π，但是想计算圆的面积。也可以通过采样的方法近似得到。随机再下图所示的正方形中撒入一些点，记落入红色区域的点的个数为n1,落入白色区域的个数为n2，则四分之一圆的面积就为n1/(n1+n2).——蒙特卡洛思想

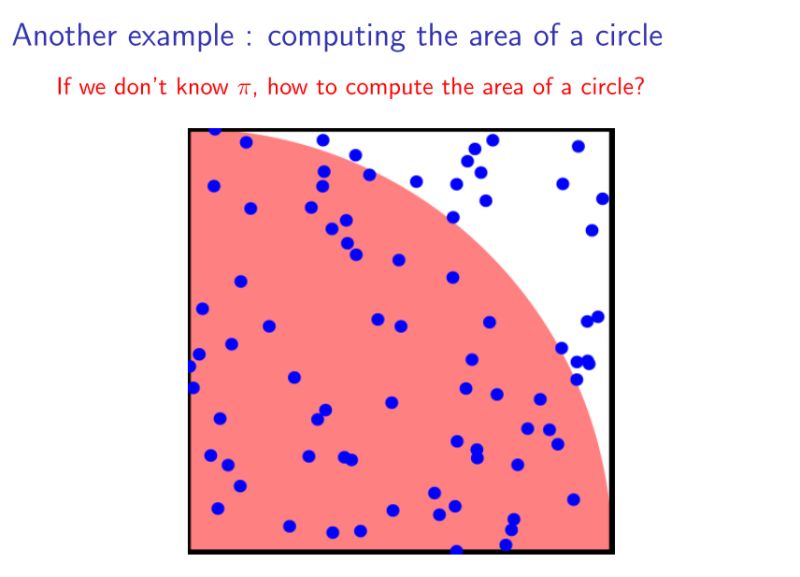
 那么，如何对连续函数估计呢？采样n多个数据，逼近最后的积分值。

 假设我们要计算 f(x)的期望值， 我们也有p(x)这种分布，这个时候我们就可以不断的从p(x)这个分布里做一些采样，比如 x1,x2,...xn, 然后用这些采样的值去算f(x),  所以最后得到的结果就是 (f(x1) + f(x2),, + f(xn))/ n

然鹅，上面例子中提到的采样都是独立的。也就是每个样本跟其他的样本都是独立的，不影响彼此之间的采样。然而，在现实问题上，有些时候我们想加快有效样本的采样速度。这个问题讨论的就是怎么优化采样过程了，也是机器学习里一个比较大的话题了。

 重申一下，用上面提到的采样方式我们可以去近似估计复杂的积分，也可以计算圆的面积，也可以计算全国人口的平均身高。但这个采样方式是独立的，有些时候，我们希望我们用更少的样本去更准确的近似某一个目标，所以就出现了sampling这种一个领域的研究，就是在研究以什么样的方式优化整个采样过程，使得过程更加高效。

 

 MCMC这种采样方法，全称为markov chain monte carlo采样方法，就是每个采样的样本都是互相有关联性的。

 但是MCMC算法需要在整个数据集上计算。也就是说为了得到一个样本，需要用所有的数据做迭代。这样当N很大时，显然不适用。而且限制了贝叶斯方法发展的主要原因就是计算复杂度太高。因此现在贝爷第领域人们最关心的问题是：怎么去优化采样，让它能够在大数据环境下学习出贝叶斯模型？

降低迭代复杂度的一个实例：

对于逻辑回归，使用梯度下降法更新参数时，有批量梯度下降法（即使用整个数据集去更新参数），为了降低计算复杂度，人们使用了随机梯度下降法，即随机从数据集中选取样本来更新参数。

所以，能否将此思想用于MCMC采样中呢？

Yes！langevin dynamic（MCMC算法中的一种），和stochastic optimizaiton(比如随机梯度下降法)可以结合在一起用。这样，我们就可以通过少量的样本去做采样，这个时候采样的效率就不在依赖于N了，而是依赖于m, m是远远小于N。