如何理解L1正则化（稀疏）和L2正则化（平滑）

上一篇文章说到使用高阶多项式来拟合非线性的数据可能会带来系数过大造成过拟合的问题，因此我们可以为损失函数增加复杂度的惩罚因子，其中 λ 越大，则惩罚力度越大：

$lambda sum_{j=1}^{n} theta_{j}^{2}$

我们称之为正则项，即用参数的平方加和，这样的形式也叫做 L2 正则( L2-norm )。 使用 L2 正则的损失函数为：

$J(vec{theta})=frac{1}{2} sum_{i=1}^{m}left(h_{vec{theta}}left(x^{(i)}right)-y^{(i)}right)^{2}+lambda sum_{j=1}^{n} theta_{j}^{2}$

由于正则化项的存在，在优化 J 的同时还得保证正则化项不至于太大，因此可以平缓曲线，达到降低过拟合的效果。

类似的，也有 L1 正则，表达式为：

$J(vec{theta})=frac{1}{2} sum_{i=1}^{m}left(h_{tilde{theta}}left(x^{(i)}right)-y^{(i)}right)^{2}+lambda sum_{j=1}^{n}left|theta_{j}right|$

二者有什么特点呢？L1 正则化具有特征选择的功能；加入 L2 正则化后仍然是凸函数方便进行最优值的求解；

如果把二者结合起来，就可以形成 “ Elastic Net ”，其中 p 指定了 L1, L2 正则化的权重:

$J(vec{theta})=frac{1}{2} sum_{i=1}^{m}left(h_{vec{theta}}left(x^{(i)}right)-y^{(i)}right)^{2}+lambdaleft(rho cdot sum_{j=1}^{n}left|theta_{j}right|+(1-rho) cdot sum_{j=1}^{n} theta_{j}^{2}right)$

加入不同的正则项后，最终得到的模型如下图所示，确实起到了防止过拟合的作用：

---

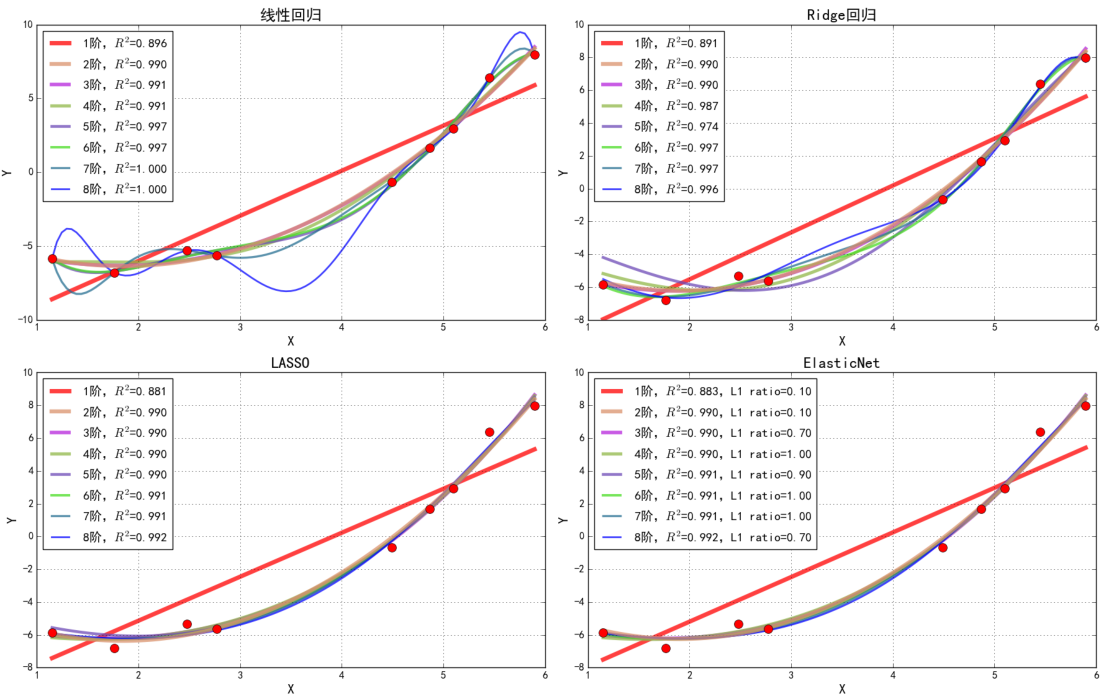
为什么会有这样的效果？

角度一：从梯度下降公式来看

上面提到了L1 正则化具有特征选择的功能，是因为进行梯度下降的时候需要求导获得梯度，假如需要学习的参数只有一个θ，那么更新参数的表达式为：

$theta=theta-alpha frac{partial}{partial theta} J(theta)$

假设求导后的系数为1，对 L1 和 L2 求导得到（其中sign( a ) 表示在 a<0, a=0, a>0 时分别取 -1, 0, 1）：

$frac{d L_{1}(θ)}{d θ}=operatorname{sign}(θ)$

$frac{d L_{2}(θ)}{d θ}=θ$

他们的图像如下：

可以看到 L1 的倒数在0的附近梯度的绝对值是1，那么每次更新时，它都是稳步向0前进，只要迭代次数足够多，那么这个参数 θ 就有可能变成 0。当然实际上模型的参数基本上不会只是一个θ而已，可能是 θ0， θ1， θ2 ... θn：

$h_{theta}(x)=sum_{i=0}^{n} theta_{i} x_{i}$

在 L1 正则化的作用下，参数 θi 就有可能变成 0 ，也就是能够剔除特征 xi 在模型中的作用，达到了稀疏特征与特征选择的作用。

而 L2 的话，就会发现它的梯度会越靠近 0，就变得越小，大部分特征对应的参数将是一个接近于 0 的数，达到了平滑特征的作用。

角度二：从几何空间来看

首先，我们把加入正则项的公式换一个角度来看，也就是带约束条件的极值求解：

$f = frac{1}{2} sum_{i=1}^{m}left(h_{vec{theta}}left(x^{(i)}right)-y^{(i)}right)^{2} min , J(vec{theta}) Leftrightarrow min , f , , quad s.t. , sum_{j=1}^{n}left|theta_{j}right| < C_{1}$

带 L1 正则项的公式如上，约束条件是要让 θ 绝对值的和足够小，边界是 C1 。

为了更直观的理解，假设每个样本的参数只有两个，θ1 和 θ2，那么约束边界的图像如下图黄线部分所示，两个坐标轴是参数 θ 的两个分量 θ1，θ2：

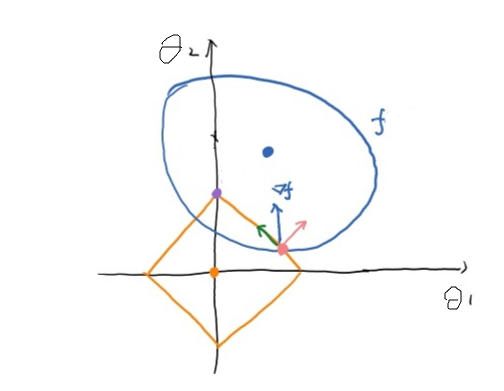
上图中的大圈是所有 f 取值相同的点构成的等值线，中间的蓝色点是 f 的最小值点，正则项与 f 的粉色交点除有三个向量：蓝色的是 f 梯度下降的方向，粉色是挣脱约束边界的方向，为了在约束条件下降低 f 的值，那么 f 只能沿着绿色的方向进行梯度下降，直到顶点（0, C1）处：

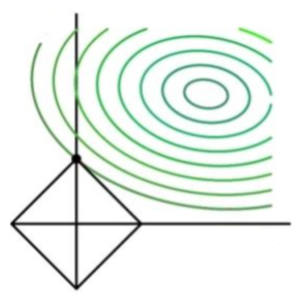
此时 f 已经在约束条件下到达最优值点，并且发现此时分量 θ1 为0，意味着 θ1 对应的特征不起作用，达到了特征选择的作用。

对于 L2 正则化而言，公式如下：

$min , J(vec{theta}) Leftrightarrow min , f , , quad s.t. , sum_{j=1}^{n} theta_{j}^{2}$

图像如下：

当 f 在约束下到底紫色的点时，梯度下降的方向和挣脱约束的方向一致，达到了最优值点：

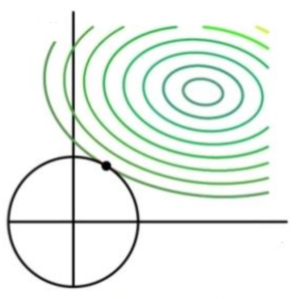
此时两个分量 θ1，θ2 的取值都比较小，避免了因为模型复杂导致的参数大小波动大的问题，起到了平滑的作用。

---

参考链接：

为什么L1稀疏，L2平滑？

l1 相比于 l2 为什么容易获得稀疏解？

L1 正则与 L2 正则的特点是什么，各有什么优势