BP算法:
1.是一种有监督学习算法,常被用来训练多层感知机。
2.要求每个人工神经元(即节点)所使用的激励函数必须可微。
(激励函数:单个神经元的输入与输出之间的函数关系叫做激励函数。)
(假如不使用激励函数,神经网络中的每层都只是做简单的线性变换,多层输入叠加后也还是线性变换。因为线性模型的表达能力不够,激励函数可以引入非线性因素)
下面两幅图分别为:无激励函数的神经网络和激励函数的神经网络


如图所示,加入非线性激活函数后的差异:上图为用线性组合逼**滑曲线来分割*面,下图为使用*滑的曲线来分割*面。

3.该算法特别适合用来训练前馈神经网络。
前馈神经网络:人工神经网络中的一种。在此种神经网络中,各神经元从输入层开始,接收前一级输入,并输入到下一级,直至输出层。整个网络中无反馈,可用一个有向无环图表示。按照层数划分,可以分为单层前馈神经网络和多层前馈神经网络。常见前馈神经网络有:感知机(perceptions)、BP(Back Propagation 反向传播)网络、RBF(Radial Basis Function 径向基)网络等。
一般看到的神经网络是这样的:

计算的时候: 信号从输入---》输出的过程是向前传递的。
信号从输入---》输出的过程是向前传递的。
那么反馈从哪里来?
在我们的网络没训练好的时候,输出的结果肯定和想象的不一样,这时候求偏差,并且把偏差一级一级的向前传递,逐层得到 ,这就是反馈。反馈是用来求偏导数的,而偏导数是用来作梯度下降的,梯度下降又是为了求得代价函数的极小值,使得期望和输出之间的误差尽可能的减小。(自己也可以定义一个代价函数,没准就不需要反馈了呢~)
,这就是反馈。反馈是用来求偏导数的,而偏导数是用来作梯度下降的,梯度下降又是为了求得代价函数的极小值,使得期望和输出之间的误差尽可能的减小。(自己也可以定义一个代价函数,没准就不需要反馈了呢~)
4.主要由两个环节(激励传播、权重更新)反复循环迭代,直到网络对输入的响应达到预定的目标范围为止。
激励传播:
在每次迭代中的传播环节包含两步:
1.(前向传播阶段)将训练输入送入到网络中,以获得激励响应。
2.(反向传播阶段)将激励响应与训练输入对应的目标输出求差,从而获得隐层和输出层的响应误差。
权重更新:
对于每个突触上的权重,按照以下步骤进行更新:
1.将输入激励和响应误差相乘,从而获得权重的梯度。
2.将这个梯度乘上一个比例(这个比例将会影响到训练过程的速度和效果,因此称为‘训练因子’。梯度的方向指明了误差扩大的方向,因此在更新权重的时候需要对其取反,从而减小权重引起的误差)并取反后加到权重上。
综上:
反向传播算法的思路如下:给定一个样例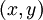 ,我们首先进行“前向传导”运算,计算出网络中所有的激活值,包括
,我们首先进行“前向传导”运算,计算出网络中所有的激活值,包括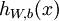 的输出值。之后,针对第
的输出值。之后,针对第 层的每一个节点
层的每一个节点  ,我们计算出其“残差”
,我们计算出其“残差”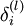 ,该残差表明了该节点对最终输出值的残差产生了多少影像。对于最终的输出节点,我们可以直接算出网络产生的激活值与实际值之间的差距,我们将这个差距定义为
,该残差表明了该节点对最终输出值的残差产生了多少影像。对于最终的输出节点,我们可以直接算出网络产生的激活值与实际值之间的差距,我们将这个差距定义为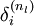 (第
(第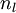 层表示输出层)。对于隐藏单元我们如何处理呢?我们将基于节点(译者注:第
层表示输出层)。对于隐藏单元我们如何处理呢?我们将基于节点(译者注:第 层节点)残差的加权*均值计算
层节点)残差的加权*均值计算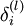 ,这些节点以
,这些节点以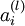 作为输入。
作为输入。
重要参考http://www.cnblogs.com/Crysaty/p/6126321.html