T1:给定一个字符串a和一个字符串b,b是a的前缀
若在b串后添加一个字符x,求a串的前缀与b串的后缀的最长相同长度。
(lb <= la <= 2*lb lb <= 100,000)
kmp裸题。。。
然而考试时没看清数据范围,只开了两倍的 lb ,91分再见
于是扔一波板子
1 for(int i=2;i<=n;i++) { 2 int p=i-1; 3 while(p&&s[i]!=s[nxt[p]+1]) p=nxt[p]; 4 if(s[i]==s[nxt[p]+1]) nxt[i]=nxt[p]+1; 5 else nxt[i]=0; 6 }
T2:给定一张n个点m条边的无向图,求从1走到n的必经点。
(n <= 200,000 m<=2*n)(可能会有自环和重边)
一看必经点,显然是裸 tarjan,开开心心5分钟打完 tarjan 求割点的板子,输出所有割点,然后跑过样例就去看T3 :)
T3想不出来,闲的无聊开始造T2的数据,结果造了随便一组就把自己干掉了。。。
如图:
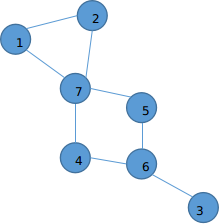
尴尬的发现割点不一定是必经点!
所以 Ctrl+A ,Delete :(
(重构是好的 o_o#)
重新构思,还是要 tarjan ,涉及到割点,又不是简单的计算和判定,那就是点双缩点或圆方树了
然而学会圆方树后就从没写过复杂,细节多,占空间大,又难写的点双缩点了
于是开始想怎么用圆方树计算答案
因为圆方树会将原图变成树,容易发现答案就是圆方树上从1到n的链上的圆点
所以做完了
什么?你说你还不会圆方树?
来康 小粉兔的博客
什么?你还不会tarjan? 请跳过这道题……

1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 #include<vector> 7 #include<queue> 8 #define ll long long 9 using namespace std; 10 const int MAXN=200005; 11 int T,n,m,dfn[MAXN],low[MAXN],stk[MAXN],fa[MAXN*2],num,tp,dcc_cnt; 12 bool flag; 13 inline int R() { 14 int a=0;char c=getchar(); 15 while(c>'9'||c<'0')c=getchar(); 16 while(c>='0'&&c<='9')a=a*10+c-'0',c=getchar(); 17 return a; 18 } 19 struct node { 20 int to,nxt; 21 }mp[MAXN*8]; 22 int h[MAXN*2],tot; 23 void add(int x,int y) { 24 mp[++tot].to=y;mp[tot].nxt=h[x];h[x]=tot; 25 } 26 void tarjan(int u) { 27 dfn[u]=low[u]=++num; 28 stk[++tp]=u; 29 for(int i=h[u];i;i=mp[i].nxt) { 30 int v=mp[i].to; 31 if(!dfn[v]) { 32 tarjan(v); 33 low[u]=min(low[u],low[v]); 34 if(low[v]==dfn[u]) { 35 ++dcc_cnt; 36 int tmp; 37 do { 38 tmp=stk[tp--]; 39 add(dcc_cnt+n,tmp); add(tmp,dcc_cnt+n); 40 }while(tmp!=v); 41 add(dcc_cnt+n,u); add(u,dcc_cnt+n); 42 } 43 } 44 else low[u]=min(low[u],dfn[v]); 45 } 46 } 47 void dfs(int u) { 48 if(u==n) { 49 flag=1; 50 return; 51 } 52 for(int i=h[u];i;i=mp[i].nxt) { 53 int v=mp[i].to; 54 if(v==fa[u]||(u<=n&&v<=n)) continue; 55 fa[v]=u; 56 dfs(v); 57 if(flag) return; 58 } 59 } 60 int main() { 61 T=R(); 62 while(T--) { 63 n=R();m=R(); 64 for(int i=1,aa,bb;i<=m;i++) { 65 aa=R(),bb=R(); 66 add(aa,bb); add(bb,aa); 67 } 68 tarjan(1); 69 dfs(1); 70 int p=fa[n]; 71 tp=0; 72 while(p!=1) { 73 if(p<n) stk[++tp]=p; 74 p=fa[p]; 75 } 76 sort(stk+1,stk+tp+1); 77 printf("%d ",tp); 78 for(int i=1;i<=tp;i++) printf("%d ",stk[i]); 79 printf(" "); 80 memset(dfn,0,sizeof(dfn)); 81 memset(low,0,sizeof(low)); 82 memset(h,0,sizeof(h)); 83 memset(fa,0,sizeof(fa)); 84 num=0;tot=0;tp=0;flag=0;dcc_cnt=0; 85 } 86 return 0; 87 }
T3:T组数据,给一个环,环上有n个物品,物品有两种颜色,每次操作可以交换相邻的两个物品
求使相同颜色的物品全部相邻的最少操作次数
(T<= 10 n <= 1,000,000)
显然正解 O ( n ) 然而想想后会发现只会写暴力模拟
再仔细一想发现好像模拟都不会写……
没办法,因为不会模拟,所以只能想想怎么计算
首先可以将一种颜色看作物品,另一种看作空位,原操作相当与移动物品
思考之后,会发现如果断环成链,那么一种方案就等价于:
在序列上选一段长度为n的子序列,再在中间选择一个断点
然后将断点左侧的物品都向左移,右侧的向右移,使其都靠在两边,代价最小。
显然以上述思路,复杂度可以做到 O ( (找区间复杂度)×(找断点复杂度)×(计算代价复杂度) )
如果枚举区间和断点的话,复杂度就为O ( n2 ×(计算代价复杂度) )
那么就想如何将计算代价做到 O ( 1 )
发现如果 O ( n ) 预处理前缀k个点移到最左和后缀k个点移到最右的代价,即前缀和后缀
我们就可以在 O ( 1 ) 计算出某段代价(可以手玩几组数据,自己想一想)
那么我们就可以做到 O ( n2 ) 的复杂度了
再仔细一想对于每个区间来说,断点位置和代价组成的函数应该是一个单谷的函数(虽然并不严格单调)
那么我们就可以用三分来优化查找断点的复杂度
我们的复杂度就会变为O ( n log(n) )
(实际上是不正确的,因为不严格单调实际上并不能用三分来计算,但复杂度更优,可以拿来水分)
最后发现枚举区间的复杂度无法优化,只能继续优化查找断点的复杂度
于是经过严谨的证明(猜的,想打表证明我也不拦你),发现断点对于所有的区间满足单调性
于是用一个指针来维护断点位置,每次暴力移动就好了
复杂度为 O ( n )

1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 #include<vector> 7 #include<queue> 8 #define ll long long 9 using namespace std; 10 const int MAXN=1000005; 11 int T,n,pos; 12 ll suml[MAXN*2],sumr[MAXN*2],ans=0x3f3f3f3f3f3f3f3f; 13 int bcntl[MAXN*2],bcntr[MAXN*2],rcnt[MAXN*2]; 14 char s[MAXN*2]; 15 inline void R() { 16 char c=getchar(); 17 while(c!='B'&&c!='R') c=getchar(); 18 while(c=='B'||c=='R') s[++n]=c,c=getchar(); 19 } 20 ll calcl(int l,int r) { 21 return suml[r]-suml[l-1]-(ll)bcntl[l-1]*(rcnt[r]-rcnt[l-1]); 22 } 23 ll calcr(int l,int r) { 24 return sumr[l]-sumr[r+1]-(ll)bcntr[r+1]*(rcnt[r]-rcnt[l-1]); 25 } 26 ll js(int l,int p,int r) { 27 return calcl(l,p)+calcr(p+1,r); 28 } 29 ll find(int l,int r) { 30 while(pos<2*n) 31 if(js(l,pos+1,r)<=js(l,pos,r)) pos++; 32 else break; 33 return js(l,pos,r); 34 } 35 int main() { 36 scanf("%d",&T); 37 while(T--) { 38 R(); 39 for(int i=1;i<=n;++i) s[n+i]=s[i]; 40 suml[0]=0; bcntl[0]=rcnt[0]=0; 41 42 for(int i=1;i<=n*2;++i) { 43 suml[i]=suml[i-1]; 44 bcntl[i]=bcntl[i-1]; rcnt[i]=rcnt[i-1]; 45 if(s[i]=='B') ++bcntl[i]; 46 else ++rcnt[i]; 47 if(s[i]=='R') suml[i]+=bcntl[i]; 48 } 49 sumr[2*n+1]=0; bcntr[2*n+1]=0; 50 for(int i=2*n;i>=1;i--) { 51 sumr[i]=sumr[i+1]; 52 bcntr[i]=bcntr[i+1]; 53 if(s[i]=='B') ++bcntr[i]; 54 else sumr[i]+=bcntr[i]; 55 } 56 pos=1; 57 for(int i=1;i<=n;i++) 58 ans=min(ans,find(i,i+n-1)); 59 printf("%lld ",ans); 60 n=0;ans=0x3f3f3f3f3f3f3f3f; 61 } 62 return 0; 63 }
