模拟赛考完,感觉自己数论弱爆了,来写写总结。
QAQ
1.exgcd
先写写推导过程吧:
对于方程 ax+by = gcd(a,b) 和 bx’+(a%b)y‘ = gcd(b,a%b)
因为 gcd(a,b) == gcd(b,a%b)
所以 ax+by == bx’+(a%b)y‘
拆开,再合并得: ax+by == ay'+b(x'-[a/b]*y')
so , code
1 int exgcd(int a,int b,int &x,int &y) 2 { 3 if(!b) 4 { 5 x=1; y=0; 6 return a; 7 } 8 int g=exgcd(b,a%b,y,x); 9 y-=a/b*x; 10 return g; 11 }
2.CRT
中国剩余定理CRT(Chinese Remainder Theorem)
中国剩余定理给出了以下的一元线性同余方程组:
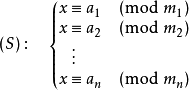
有解的判定条件,并用构造法给出了在有解情况下解的具体形式。
在模![]() 的意义下,方程组
的意义下,方程组![]() 只有一个解:
只有一个解:
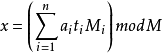 ——百度百科
——百度百科
具体说说,如果我们要构造一个合法解,那么考虑对于其中任意的一个方程 i ,应该如何构造:
首先,我们要保证 x mod mi == ai 那么x 应该加上 ai ,但会发现这会对其他方程产生影响
所以为了消除对其他方程的影响,我们应该加上 ai × ( M/mi ) ,但又会发现 x 又不满足mod mi 余 ai 了
所以实际我们应该给 x 加上 ai × (M/mi) × (M/mi)-1 ,(这个逆元是mod mi 意义下的)
so,code
1 int CRT() 2 { 3 int M=1,x=0; 4 for(int i=1;i<=n;i++) M*=m[i]; 5 for(int i=1;i<=n;i++) 6 { 7 int tmp=M/m[i]; 8 int t=qpow(tmp,m[i]-2,m[i]); 9 x=(x+a[i]*tmp*t)%M; 10 } 11 return x; 12 }
3.Lucas
当遇到组合数的计算时,若模数小于计算中阶乘的数时,不能直接对阶乘取模,此时便需要用到Lucas定理:
$ C_n^m equiv C_{n/p} ^ {m / p} imes C_{n\%p}^{m\%p} mod p $ (p为质数)
当 n,m 均小于p时计算,一直递归就行了
so,code
1 int C(int n,int m) 2 { 3 if(n<m) return 0 4 return fac[n]*inv[m]%p*inv[n-m]%p; 5 } 6 int Lucas(int n,int m) 7 { 8 if(n<m) return 0; if(!n) return 1; 9 return Lucas(n/p,m/p)*C(n%p,m%p)%p; 10 }