转自：https://zhuanlan.zhihu.com/p/37605060
目录：
- 前言
- 偏相关或复相关
- 意义与用途
- 分析方法：
- 1、 样本相关系数矩阵、相关系数检验
- 2、 复相关分析
- 3、 决定系数
（RMSE的介绍）
- 小结
一、前言：
继上一篇文章，继续探讨相关性分析，这次不再是两个变量，而是3个或者以上的变量之间的相关关系分析。
没读过上篇文章请先仔细阅读再过来，因为多变量本质上是基于双变量的
TzeSing Kong：相关性分析(两变量)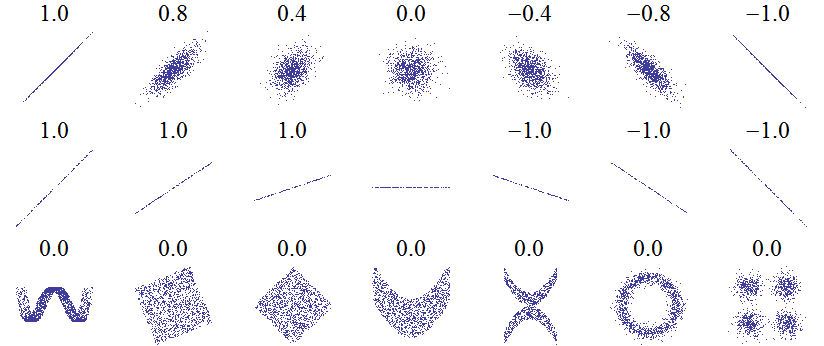
二、偏相关或复相关
简单相关：研究两变量之间的关系
偏相关或复相关：研究三个或者以上变量与的关系
在这里仍然是选择最简单的线性相关来解释：
三、意义与用途：
有些情况下，我们只想了解两个变量之间是否有线性相关关系，并不想拟合建立它们的回归模型，也不需要区分自变量和因变量，这时可用相关性分析。
四、分析方法：
1、样本相关阵
设 来自正态总体
容量为
的样本，其中每个样本
有
个观测
分别计算两两样本之间的简单相关系数 ，它们构成的矩阵就是：
由于每个变量跟自己的相关系数就是 ，即：
其中， 就是两个变量的简单相关系数。
例子：
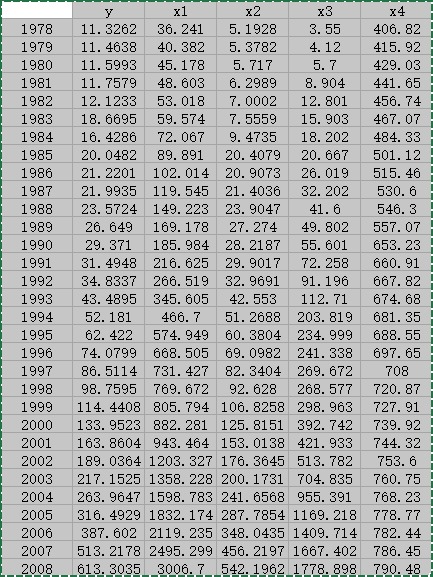
> X <- read.table("clipboard", header = T)
> cor(X) # 相关系数矩阵
y x1 x2 x3 x4
y 1.0000000 0.9871498 0.9994718 0.9912053 0.6956619
x1 0.9871498 1.0000000 0.9907018 0.9867664 0.7818066
x2 0.9994718 0.9907018 1.0000000 0.9917094 0.7154297
x3 0.9912053 0.9867664 0.9917094 1.0000000 0.7073820
x4 0.6956619 0.7818066 0.7154297 0.7073820 1.0000000再看看矩阵散点图：
> pairs(X, ...) # 多元数据散点图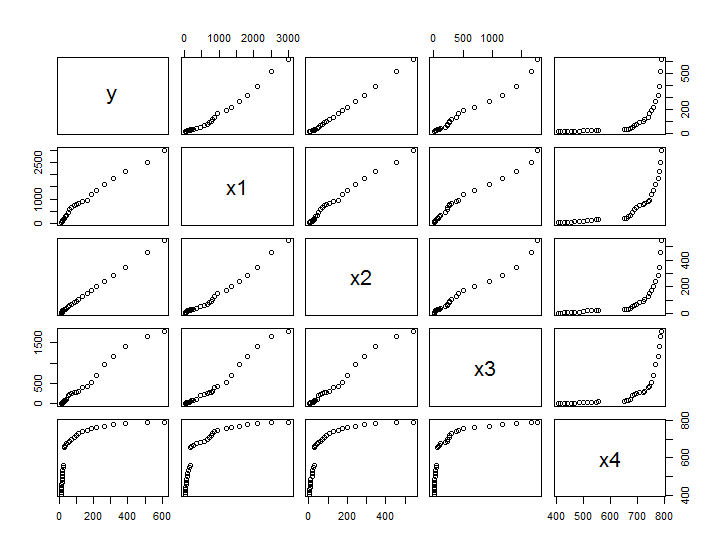
相关系数检验：
> install.package('psych') # 先安装一个'psych'的包
> library(psych)
> corr.test(X)
Call:corr.test(x = yX)
Correlation matrix
y x1 x2 x3 x4
y 1.00 0.99 1.00 0.99 0.70
x1 0.99 1.00 0.99 0.99 0.78
x2 1.00 0.99 1.00 0.99 0.72
x3 0.99 0.99 0.99 1.00 0.71
x4 0.70 0.78 0.72 0.71 1.00
Sample Size
[1] 31
Probability values (Entries above the diagonal are adjusted for multiple tests.)
y x1 x2 x3 x4
y 0 0 0 0 0
x1 0 0 0 0 0
x2 0 0 0 0 0
x3 0 0 0 0 0
x4 0 0 0 0 0
To see confidence intervals of the correlations, print with the short=FALSE option
上面矩阵是相关系数的 值矩阵，下面矩阵是
值矩阵
可以看出 与
的关系都十分密切
相关系数 且置信度
2、复相关分析
实际分析中，一个变量( )往往要受到多种变量(
)的综合影响，
所谓复相关，就是研究多个变量同时与某个变量的相关关系，
度量复相关程度的指标是复相关系数
多个变量同时与某个变量的相关关系不能直接测算，只能通过间接测算
复相关系数的计算：
设因变量 ，自变量为
，构造一个线性模型为：
对 与
作相关分析，就是对
与
做简单相关分析
记：
为
与
的复相关系数，
为
的简单相关系数
的计算公式：
复相关系数常用于多元线性回归分析中，我们希望知道因变量与一组自变量之间的相关程度，即复相关，复相关系数反映了一个变量与另一组变量的密切程度。
假设检验：
与多元回归的方差分析一样，所以我留在下篇文章阐述回归分析与方差分析的时候会继续详细说明
综上：
至于 和
还有
是什么？
就由下篇文章阐述回归分析的时候会详细说明。
TzeSing Kong：线性回归——描述变量间预测关系最简单的回归模型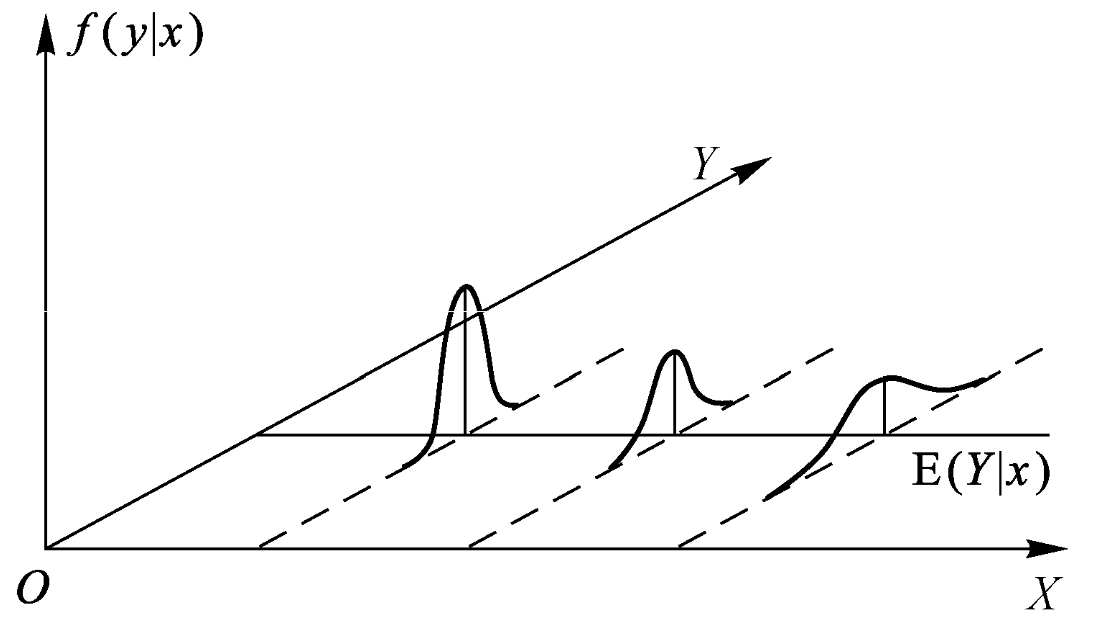
3、决定系数 （coefficient of determination）
在复相关系数中，根号里面的比值 ，
其实说明了回归平方和与总离差平方和的比值，反应了回归贡献的百分比
把复相关系数两边平方一下就能得到决定系数
决定系数用于评价多元回归方程、变量选择、曲线回归方程拟合的好坏程度中，常常用到。
【注意】
，如果一个模型的
，
，但是另一个测试集
(分母小了，
。变成了模型好坏取决于测试集的波动程度，所以这个十分不靠谱
- 不明白上面的话，可以再看一个例子，如果我们建立了一个模型预测广州房价，如果测试集中广州房屋售价的波动范围较大——方差较大（40万-几千万），因为方差大，所以很可能导致
），但
可能十万，这对于广州房价预测来说是一个很糟糕的预测范围。
具体用法，留在回归分析中详细阐述。
TzeSing Kong：线性回归——描述变量间预测关系最简单的回归模型在 线性回归 中的 3.4 决定系数
# 先建立多元线性回归模型
> fm = lm(y~x1+x2+x3+x4,data = X)
计算多元线性回归模型决定系数
> R2 = summary(fm)$r.sq
> R2
[1] 0.9997162
计算复相关系数
> R = sqrt(R2)
> R
[1] 0.9998581
【补】
什么是RMSE？
RMSE是回归问题的性能指标，衡量的是 预测值 与 真实值
间的差距
是测量预测误差的标准差
举例子：RMSE 等于 50000，根据【 准则】意味着：
大约 68% 的预测值位于真实值的 50000元（ ）以内，
大约 95% 的预测值位于真实值的 100000元 （ ）以内，
大约 99.7% 的预测值位于真实值的 150000元内 （ ）以内
五、小结：
可以看出多变量相关分析跟回归分析的关系很密切，多变量相关分析能为回归分析服务，因为要具有相关性才有做线性回归拟合的价值