链表的基本操作
链表的基础操作有查找、删除、添加。
查找
先定义一下链表的数据结构:
class DataNode{
int key;
int value;
DataNode pre;
DataNode next;
public DataNode(){};
public DataNode (int key,int value){
this.key = key;
this.value = value;
}
}

其中的key和value就是节点实际存储的值。pre和next分别指向前一个节点和下一个节点。一般的单向链表只有next,我这里定义的是双向链表。查找操作就是从头节点,一直遍历next,直到找到目标节点为止。可以用while循环或者递归实现,找到目标节点就跳出或返回即可,时间复杂度为O(n)。
删除
以上面的双向链表为例,演示一下删除操作。我们假设有三个节点A、B、C,现要删除B节点。把A.next指向C,C.pre指向A。中间的B节点就不在链路上了,会被垃圾收回器给回收掉。
public void delNode(DataNode node){
node.pre.next = node.next;
node.next.pre = node.pre;
}
上面的代码初看可能有点绕,其实链表除了查找操作,都有点绕,建议画图理解。其中node.pre.next就是上一个节点的下一个节点,把它改成node.next,就相当于让上一个节点指向自己的下一个节点。第二行代码就是让下一个节点的pre指向自己的上一个节点。删除操作的时间复杂度为O(1)。
添加
假设有A、C两个节点,现要往中间添加一个B节点。思路看图都能想到,你的写法不一定要和我一样,只是注意别丢失节点了,代码如下:
//写法1
public void addNode(DataNode pre,DataNode node){
//先记录一下pre.next节点,否则下一步会丢失C节点
DataNode next = pre.next; // 记录C
pre.next = node; //A->B
node.next = next; //B->C
next.pre = node; // B<-C
node.pre = pre; // A<-B
}
//写法2,不用临时变量
public void addNode(DataNode pre,DataNode node){
node.next = pre.next; //B->C
node.pre = pre; //A<-B
pre.next = node; // A->B
node.next.pre = node; //C<-B
}
算法题
LRU缓存
关于链表的算法题中,我觉得最能训练链表操作的就是LRU缓存。即给出已给固定容量的容器,往里put元素时,如果容量到达最大,就删除最久未使用的元素。
题目描述:
实现 LRUCache 类:
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
思路:根据key找到value,所以肯定要一个Hash表存储值。元素数量超过capacity就要删除最久未使用的关键字。我们就设计一个链表,每次get元素A时,就把A移到链表头部。需要删除元素时,直接删除链表尾部的元素,尾部的就是最久没使用的。
每次get时要把对应的元素移至头部,为了避免遍历链表,设计Hash表的value类型可以设置成DataNode,这样就免去的链表查找的时间。DataNode就复用开头定义的数据结构。
class LRUCache {
int capacity;
HashMap<Integer,DataNode> map;
//定义一个虚拟的头节点和尾节点,方便删除尾节点和往头节点添加元素
DataNode head;
DataNode tail;
//1.初始化相关属性
public LRUCache(int capacity) {
this.capacity = capacity;
map = new HashMap<>();
head = new DataNode();
tail = new DataNode();
head.next = tail;
tail.pre = head;
}
//2.实现get逻辑,里面的moveToHead可以先不实现
public int get(int key) {
DataNode node = map.get(key);
if(node==null){
return -1;
}
//把node节点移至头部
moveToHead(node);
return node.value;
}
//3.实现put逻辑
public void put(int key, int value) {
if(map.containsKey(key)){
//如果当前key已经存在
DataNode node = map.get(key);
moveToHead(node);
node.value = value;
}else{
//不存在就新建一个node,如果超过capacity就删除尾部节点
DataNode node = new DataNode(key,value);
map.put(key,node);
if(map.size()>capacity){
//因为还要从map中删除元素,所以removeTail要有返回值
DataNode delNode = removeTail();
map.remove(delNode.key);
}
addHead(node);
}
}
//4.最后一步,实现上面所需的链表操作方法
private void moveToHead(DataNode node){
//先删除,再移至头部
removeNode(node);
addHead(node);
}
private void addHead(DataNode node){
node.next = head.next;
node.pre = head;
head.next = node;
node.next.pre = node;
}
private DataNode removeTail(){
DataNode delNode = tail.pre;
removeNode(delNode);
return delNode;
}
//removeTail和moveToHead都有删除元素的操作,所以再提取一个删除方法
private void removeNode(DataNode node){
node.pre.next = node.next;
node.next.pre = node.pre;
}
}
反转链表
反转链表也是面试中出现频率比较高的,反转链表是个单向链表,它的操作比双向链表更简单。
题目描述:
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
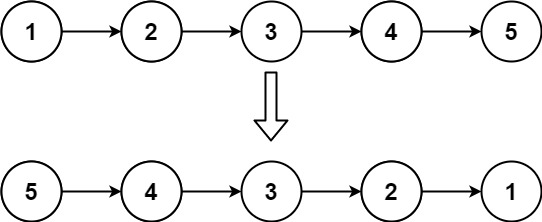
思路:定义两个指针(变量),一个指向当前节点,一个指向前一个节点。每次反转指针指向的两个节点,然后指针往后移一位。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
if(head==null||head.next==null){
return head;
}
ListNode pre = null;
ListNode node = head;
while(node!=null){
ListNode temp = node.next;
//反转node和pre
node.next = pre;
//node和pre往后移一位
pre = node;
node = temp;
}
//因为node最终会移到尾节点的next上,也就是null
//所以pre才是真正的尾节点,也就是反转后的头节点
return pre;
}
}
环形链表
题目描述:
出一个链表的head,判断该链表是否是环形链表。如果是,就返回环形的入口。如果不是,就返回null。

如上图,入口节点就是2。
思路1:要做出这个题不难,第一下就能想到:边遍历链表,边往Hash表存储节点,每次遍历前判断Hash表是否存在当前节点,如果存在,这个节点就是环形入口。如果遍历完了,还没有重复节点,就说明没有环形。时间复杂度:O(n),空间复杂度:O(n)。
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
HashSet<ListNode> set = new HashSet<>();
while(head!=null){
if(set.contains(head)){
return head;
}
set.add(head);
head = head.next;
}
return null;
}
}
思路2:优化链表的空间复杂度常用手段就是用指针,思路2就是定义两个快慢指针,属于数学逻辑范畴了。我们定义一个慢指针slow,一个快指针fast。slow一次移动一位,fast一次移动两位。
-
如果fast移到了null节点,说明链表无环,直接返回null
-
fast和slow相遇
-
- 此时fast和slow一定在环形内,否则不可能相遇。我们假设head到环形入口(不含入口)的长度为x,环形长度为y。
- 然后假设slow走了s步,则fast走了2s步(fast是slow的两倍速)
- fast和slow相遇时,fast在环内比slow多走了ny步(关键点,可以画图理解一下)
-
-
- 所以fast=2s=s+ny(s是slow走的步数,ny是fast比slow多走的步数)
- 所以s=ny
-
-
- 根据上面的推测s=ny,接着可以推算出,入口点就是x+ny。因为y是环形长度,n是正整数,所以ny实际上和y没区别,无非就是多绕了几圈。(关键点,也可以画图理解一下)。
- 此时slow已经走了ny步,所以再走x步就是入口点了。但是我们不知道x等于多少,那我们就让一个指针从head再走一遍,一次走一步,和slow相遇点就是入口点。为了少创建一个变量,可以让fast指针回到head节点重新走。
public class Solution {
public ListNode detectCycle(ListNode head) {
if(head==null||head.next==null){
return null;
}
ListNode slow = head;
ListNode fast = head;
while(true){
if(fast == null||fast.next == null){
return null;
}
slow = slow.next;
fast = fast.next.next;
//第一次相遇
if(fast==slow){
break;
}
}
fast = head;
while(fast!=slow){
fast = fast.next;
slow = slow.next;
}
return slow;
}
}
总结
链表必须要掌握它的删除、添加、查找三个基础操作。链表的类型还分为:单向链表、循环链表(头尾相连,或者带环的)、双向链表。只要掌握了双向链表的基础操作,其他链表都不在话下。
关于链表的算法中,因为不能像数组那样,通过下标随机访问,所以一般会把节点存进Hash表。如果Hash表也不想存,想优化空间复杂度,一般的做法是定义指针。单向链表一般要定义双指针,一个指向当前,一个指向前一个,如果是双向链表,只用定义一个。但是在算法题中,单纯只考链表的题目比较少,很多都会带一些其他知识点。比如链表的排序、链表的二分查找等。只要熟练掌握链表的插入、删除,只用考虑排序、查找的逻辑就行了,跟数组的排序、二分查找没啥区别。