(luogu P2365)任务安排
题目描述
(N)个任务排成一个序列在一台机器上等待完成(顺序不得改变),这(N)个任务被分成若干批,每批包含相邻的若干个任务。从时刻(0)开始,这些任务被分批加工,第(i)个任务单独完成的时间是(Ti)。每批任务开始前,机器需要启动时间(S),而完成这批任务的时间是各个任务需要时间的总和(同一批任务将在同一时刻完成)。每个任务的费用是它的完成时刻(注意,这里是累加时刻)乘以一个费用系数(Fi)。请确定一个分组方案,使得总费用最小。
输入输出格式
输入格式
(N、S)两个数(1le Nle5000,0le Sle50)
接下来(N)行每行两个数,分别为(Ti、Fi)。
输出格式
一行,最小费用
(Solution)
可以设计状态(dp[i])表示考虑到第(i)个时的最小费用。转移的时候枚举上一组最后一个(j),显然
(dp[i]=min(dp[i],dp[j]+s*(f[n]-f[j])+t[i]*(f[i]-f[j])))
其中(f[i])是费用系数的前缀和,(t[i])是需要时间的总和。(s*(f[n]-f[j]))表示累加的启动机器的时间。因为这次启动了,往后的所有机器都需要加上这段时间。(t[i]*(f[i]-f[j]))是这段区间的机器的总费用系数乘以结束时间。
我们得到了一个(O(n^2))的做法。
观察这个式子。
(dp[i]=dp[j]+s*f[n]-s*f[j]+t[i]*f[i]-t[i]*f[j])
把(min)去掉会得到这样一个式子。我要让这个式子最小。
移项得到(dp[j]=(s+t[i])*f[j]+dp[i]-s*f[n]-t[i]*f[i])
要让(dp[i])最小,即让该函数的截距最小,因为后面两个数都是常量。而该直线的斜率已定,那么就可以便利所有的合法(j)找一个最短的。显然斜率单调递增,所以可以用斜率优化。
考虑合法的点画在二维平面直角坐标系里长什么样子。
每个点的坐标都是((f[i],dp[i])),假如现在已经有一些点了,现在有一条新的直线,斜率固定,让该直线从下往上扫,当它第一次碰到有的那些点中某一个的时候,是最优的状况。
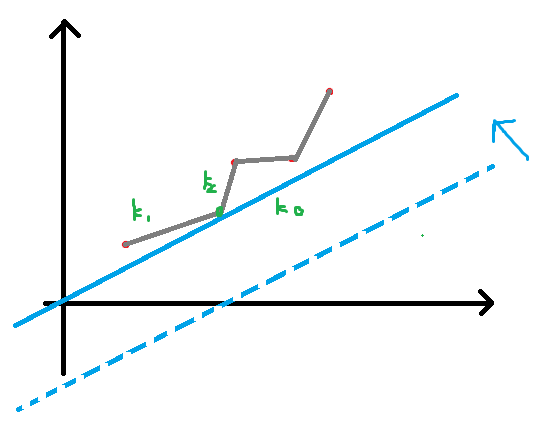
不会被选到,我们就可以把它从合法点集中去掉。同样用不到的还有第三个点。手玩一下就好。
我们用一个队列来维护这些点。更新队首的时候判断一下队首的点与第二个点的连线斜率与当前直线斜率的关系。如果小,就退队,直到大于。更新队尾,也就是加入点的时候,判断当前点与队尾的点的连线斜率与队尾的点与前一个点的连线斜率关系,如果小就退队,直到大于。
代码
#include<iostream>
#include<cstdio>
long long read(){
long long x=0;int f=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
return f?-x:x;
}
int dp[5010],t[5010],f[5010],n,s,q[5010],l,r;
int main(){
n=read(),s=read();
for(int i=1;i<=n;i++){
t[i]=read(),f[i]=read();
t[i]+=t[i-1],f[i]+=f[i-1];//前缀和
}
dp[0]=0,l=1,r=1;
for(int i=1;i<=n;i++){
while(l<r&&dp[q[l+1]]-dp[q[l]]<=(s+t[i])*(f[q[l+1]]-f[q[l]])) l++;//更新队头
dp[i]=dp[q[l]]+t[i]*f[i]+s*f[n]-f[q[l]]*(s+t[i]);
while(l<r&&(dp[i]-dp[q[r]])*(f[q[r]]-f[q[r-1]])<=(dp[q[r]]-dp[q[r-1]])*(f[i]-f[q[r]])) r--;//更新队尾
q[++r]=i;
}
printf("%d
",dp[n]);
return 0;
}