题目描述
红莲清泪两行欲吐半点却无
如初是你杳然若绯雾还在水榭畔画楼处
是谁衣白衫如初谁红裳如故
——《忆红莲》
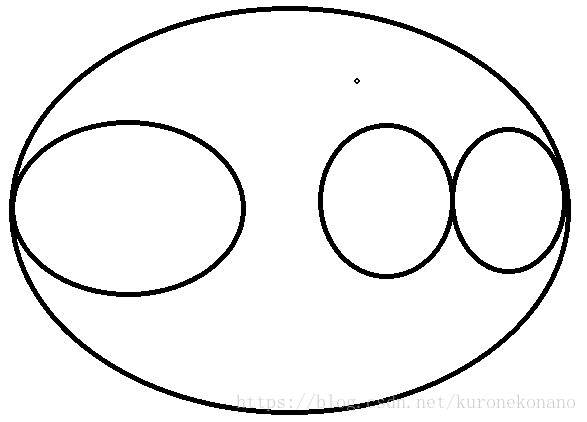
小奇想画几朵红莲,可惜它刚开始学画画,只能从画圆开始。小奇画了n个圆,它们的圆心都在x轴上,且两两不相交(可以相切)。现在小奇想知道,它画的圆把画纸分割成了多少块?(假设画纸无限大)
输入
第一行包括1个整数n。
接下来n行,每行两个整数x,r,表示小奇画了圆心在(x,0),半径为r的一个圆。
输出
输出一个整数表示答案。
样例输入
4
7 5
-9 11 11 9
0 20
样例输出
6
提示
对于 100%数据,1<=n<=300000,-10^9<=x<=10^9,1<=r<=10^9。
这题重判之后,排序后判断端点map重复标记的那个方法被hack了
因为有这个样例:
明显根据排序后会先标记大圆,然后从左到右标记小圆,这样最好一个圆就被认为是联通并分割了了大圆。
思路:首先可以在数圆的分区的时候发现,有两种情况,一是一个圆即一个分区,两圆没有任何关系,无论是外离外切还是内切内含,圆的个数即分区数量;二是当多个圆在某个圆中内含或内切的时候会将一个圆的分区分割成两块。此时原来一个圆只能构造出的一个分区就变成了两个。另外要加上无限大的纸中未被圈定的1块区域。
因此结果即 : 圆数量n+被分割圆数量ans+1
只需计算被分割圆的数量即可。先将圆按大小和从左到右的顺序排序,即算出圆的左右两位置L和R,L按从小到大排序,当L相同时按R从大到小排序。这样就形成了,整体从数轴左遍历到右。部分按照大圆到小圆的顺序遍历。
当两个圆的左端点重合时,说明两者可能有分割与被分割的关系,要做到完全分割,必须有若干个圆的左端点与右端点重合,形成一个传递的关系,大家手牵手,把一个大圆彻底分开。即,当前遍历第i个圆,当i和i+1个圆的L相同,那么可能被分割,当i右端点和i+1的左端点重合,说明正在逐渐形成分割的条件。当i的右端点和i+1的右端点重合时,说明能传递过来,即被分割。
此处用栈来记录所有左端点相同的圆,当遍历过程中出现了不连续的,没有牵手的圆,说明无法分割,将栈顶上的圆弹出,继续判断后面的圆是否会被分割。
#include<bits/stdc++.h>
using namespace std;
const int maxn=3e5+10;
int n;
struct node
{
int ll,rr;
node(){}
node(int a,int b)
{
ll=a;
rr=b;
}
bool operator <(const node &a)const
{
if(ll==a.ll)return rr>a.rr;
return ll<a.ll;
}
} a[maxn];
int x,r;
stack<int>s;
int main()
{
while(scanf("%d",&n)!=EOF)
{
int ans=0;
for(int i=0; i<n; i++) scanf("%d%d",&x,&r),a[i]=node(x-r,x+r);
sort(a,a+n);
while(!s.empty())s.pop();
for(int i=0; i<n-1; i++)
{
if(a[i+1].ll==a[i].ll)
{
s.push(i);
continue;
}
if(a[i].rr!=a[i+1].ll&&!s.empty()) s.pop();
if(!s.empty())
if(a[i+1].rr==a[s.top()].rr)
ans++,s.pop();
}
printf("%d
",n+1+ans);
}
}
写到一半发现不对劲。。。这个代码目前是能过的,但是自己找到了数据hack
hack
5
10 10
3 6
8 2
2 1
4 1
4
0 8
-4 4
-2 2
4 4
明显这个样例是会因为遍历顺序而弹出第一个大圆的,而内部两个中圆又因为遍历顺序不是相邻的而无法判断牵手
在此隆重介绍线段树解法【感谢队友zls的讲解和代码】:
离散化所有圆的左右边界,然后 用线段树进行区间更新,也是按照排序后的顺序,按照半径大小排序,半径较小的排前面,若遍历到某个圆的左右区间时,发现查询线段树,该区间被整段标记过了,那么说明这个圆是会被分割成两份的。否则,只要某个区间内存在至多一段未被标记的区间即表示该圆无法被分割。查询完后就标记该圆的区间。