1.大纲
模型选择的原则
模型的性能指标
模型评估方法
模型性能比较
一:模型选择
1.几个概念
误差
模型的预测输出值与真实值之间的差异
有测量误差与系统误差
训练
通过对已知的样本数据进行学习,从而得到模型的过程
训练误差
模型作用于训练集时的误差
泛化
由具体的,个别的扩大为一般的。对机器学习模型来讲,泛化是指模型作用于新的样本数据。
泛化误差
模型作用于新的样本数据时的误差

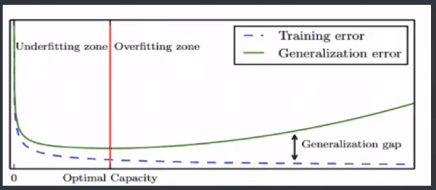
2.过拟合与欠拟合
模型容量:是指其拟合各种模型的能力
过拟合Oberfitting:某个模型在训练集上表现非常好,但是在新样本上表现很差
欠拟合Underfitting:与上面相反
3.模型选择
对一个任务,有多中模型可以选择,对一个模型有多组参数。
可以通过分析,评估模型的泛化误差,选择泛化误差最小的模型。
二:模型评估方法
1.评估思路
对模型泛化误差进行评估,选出泛化误差最小的模型。
待测试数据集全集未知,使用数据集进行测试,测试误差即为泛化误差的近似。
测试集与训练集尽可能互斥
测试集与训练集独立同分布
2.留出法Hold-out
将已知的数据集分成两个互斥的部分,其中一个用来训练模型,一个用来测试模型,评估误差,作为泛化误差的估计。
两个数据集的划分尽可能保持数据分布一致性,避免因数据划分过程引入的偏差
保持样本的类别比例相似,即采用分层采样
数据分割存在多种形式会导致不同的训练集,测试集划分,单次往往会存在偶然性,稳定性较差,往往会进行若干次随机划分,重复试验评估平均值作为评估结果
测试,训练的比例通常是7:3,8:2等。
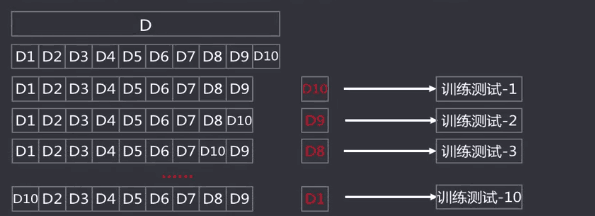
3.交叉验证法
将数据集划分K个大小相似的互斥数据子集,子集数据尽可能保证数据分布的一致性,每次从中选取一个数据集作为测试集,其余作为训练集
可以进行K次训练与测试,得到评估均值。
该方法也称作K折交叉验证。
使用不同的划分,重复P次,称为p次k折交叉验证
4.留一法
是K折交叉验证的特殊形式,将数据集分成两个,其中一个数据集记录的条数为1,作为测试集使用,其余作为训练集训练模型。
训练出的模型与使用数据全集得到的模型接近,其评估结果比较准确。
缺点是数据集比较大,训练测试与计算规模较大
5.自助法Boostrapping
是产生样本的抽样方法,其实质是有放回的随机抽样。
即从已知数据集中随机抽取一条记录,然后将该记录放到测试集同时放回原数据集,继续下一次抽样,直到测试集中的数据条数满足要求。
有些数据出现多次,有些数据不会出现。
估算,大约有0.368(总量的三分之一)数据不会被选中。
6.集中方法的使用场景
留出法
实现简单方便,在一定程度上能评估泛化误差
测试集与训练集分开,缓解了过拟合
一次划分,偶然性大
数据被拆分,用于训练与测试的数据更少了
交叉验证法
k可以根据实际情况设置,充分利用了所有的样本
多次划分,评估相对稳定
计算比较繁琐,需要K次训练和评估
自助法
样本较小可用使用产生多个样本集,且有36.8%的测试样本
对于总体的理论分布没有要求
无放回抽样引入了额外的偏差
选择
对于数据充足,采用留出法或者K折交叉验证法
对于数据较小,且难以有效划分训练集的时候,采用自助法
对于数据较小,且可以有效的划分训练集与测试集,采用留一法
三:性能度量
1.性能度量
评价模型泛化能力的标准。
对于不同的模型,有不同的评价标准,不同的评价标准将会导致不同的结果。
模型的好坏是相对的,取决于相当于当前任务需求的完成情况。
回归模型的性能度量通常选用均方误差。
2.分类算法的性能度量

3.聚类算法的性能度量

四:模型比较
1.模型比较
选择合适的评估方法和相应的性能度量,计算出性能度量后直接比较。
存在的问题:
模型评估得到的是测试集上的性能,并非严格意义上的泛化性能,两者不完全相同
测试集上的性能与样本选取关系很大,不同的划分,测试结果会不同,比较缺乏稳定性
很多模型本事就有随机性,即使参数和数据集相同,其运行结果也存在差异
五:假设检验【自己看概率统计】
1.假设检验
这个是用于模型比较的。
事先对总体的参数或者分布做一个假设,然后基于已有的样本数据去判断这个假设是否合理。
常见的假设检验有t检验法,卡方检验,F检验。
2.假设检验的步骤
建立假设
确定检验水准
构造统计量
计算P值
得到结论
六:偏差,方差与噪声
1.概念
偏差:描述的书根据样本拟合的模型的输出预测结果的期望与样本真是结果的差距,即在样本上拟合好不好
方差:模型的每一次输出结果与模型输出期望之间的误差,即稳定性
噪声:为真实标记与数据集中的实际标记见的偏差。
偏差:刻画了学习算法本身的拟合能力。通常模型越复杂,偏差越小。
方差:刻画了数据扰动造成的影响
噪声:刻画学习问题本身的难度
2.泛化误差的推导
结论:方差与偏差的和。

3.期望的模型
低偏差,低方差
4.偏差
通常模型越复杂,偏差越小。
体现了拟合的优劣
5.方差
体现的是模型的稳定性。
通常模型越简单,方差越小。