二叉树(Binary Tree)是n(n >= 0)个节点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根节点和两颗互不相交的,分别称为根节点的左子树和右子树的二叉树组成。
二叉嘛,也就是每个节点最多有两个分支。
图示:
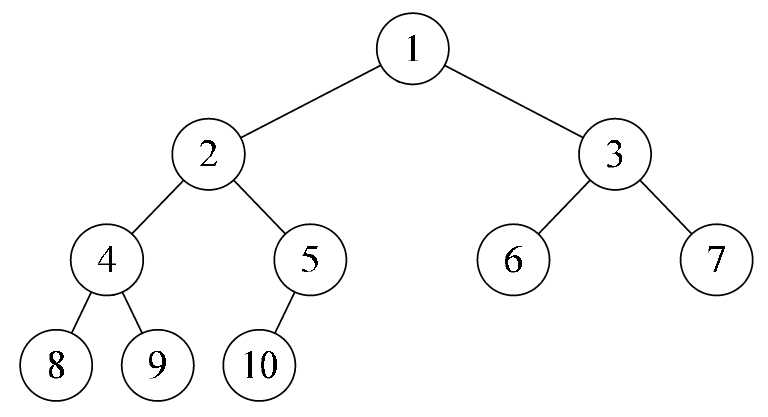
二叉树具有五种基本形态:
1.空二叉树
2.只有一个根节点
3.根节点只有左子树
4.根节点只有右子树
5.根节点既有左子树又有右子树
特殊的二叉树:
1.斜树(只有左子树的称为左斜树,只有右子树的称为右斜树,两者统称为斜树)
2.满二叉树(所有的分支节点都存在左子树和右子树,并且所得树叶都在同一层上)
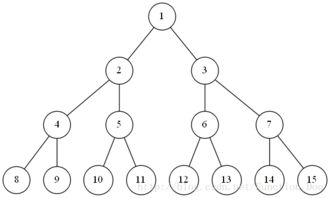
3.完全二叉树的特征:
1.叶子结点只能出现在最下两层
2.最下层的叶子一定集中在左部连续位置
3.倒数二层,若有叶子结点,一定都在右部连续位置
4.如果节点度为1(这里的度与离散数学中的度不一样,这里的度是指节点所拥有的子树数),则该节点只有左孩子,即不存在只有右子树的情况
5.同样节点数的二叉树,完全二叉树的深度最小
二叉树的性质:
性质1:在二叉树的第i层上至多有2^(i - 1)个节点(i >= 1)
性质2:深度为k的二叉树至多有2^k - 1个节点(k >= 1)
性质3:对任何一颗二叉树T,如果其终端节点数为n0,度为2的节点数为n2,则n0 = n2 + 1
性质4:具有n个节点的完全二叉树的深度为[log2n] + 1([]表示不大于x的最大整数)
性质5:如果对一颗有n个节点的完全二叉树(其深度为[long2n] + 1)的节点按层序编号(从第1层到第[log2n] + 1层,每层从左到右),对任一节点i(1 <= i <= n)有
①如果i = 1,则节点i是二叉树的根,无双亲;如果i > 1,则双亲是节点[i / 2]
②如果2i > n,则节点i无左孩子(节点i为叶子结点);否则其左孩子是节点2i
③如果2i + 1 > n,则节点i无右孩子;否则其右孩子是节点2i + 1
二叉树的存储结构同样分为两种:
一种为二叉树顺序存储结构,另一种为二叉树的链式存储结构
一般顺序存储结构只用于完全二叉树
下面我们来介绍链式存储结构的二叉树,,,
二叉链表:有一个数据域和两个指针域
以下代码实现二叉树的建立与遍历(其中有求节点为1的个数)
#include <iostream>
#include <cstdlib>
using namespace std;
int c=0;
//进行前序遍历的输入,扩展二叉树ABDC->AB#D##C##
//二叉树链表的存储结构,抄作业的同学把其他遍历方式删掉
typedef struct BiTNode
{
char data;
//节点数据
struct BiTNode *lchild, *rchild;
//左右孩子指针
} BiTNode, *BiTree;
//二叉树的建立
void CreatBiTree(BiTree &T)
{
char ch;
cin >> ch;
if (ch == '#')
T = NULL;
else
{
T = new BiTNode;
//生成根节点
if (!T)
exit(1);
T->data = ch;
CreatBiTree(T->lchild); //构造左子树
CreatBiTree(T->rchild); //构造右子树
}
}
//前序遍历
void PreOrderTraverse(BiTree T)
{
if (!T)
return;
cout << T->data;
if(T->data!='1')
c++;
//显示节点数据
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
//中序遍历
void InOrderTraverse(BiTree T)
{
if (!T)
return;
InOrderTraverse(T->lchild);
cout << T->data;
//显示节点数据
InOrderTraverse(T->rchild);
}
//后序遍历
void PostOrderTraverse(BiTree T)
{
if (T == NULL)
return;
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
cout << T->data;
//显示节点数据
}
int GetHeight(BiTree tree){
int maxn=0;
if(tree==NULL)
{
return 0;
}
else
{
int left_height=GetHeight(tree->lchild);//左子树高度
int right_height=GetHeight(tree->rchild); //右子树高度
maxn=left_height; //比较左右子树的最大高度
if(right_height>maxn)
maxn=right_height;
}
return maxn+1; //算上跟节点,子树高度加1返回
}
int main()
{
BiTree tree;
cout<<"建立二叉树:"<<endl;
CreatBiTree(tree);
cout<<"遍历二叉树"<<endl;
PreOrderTraverse(tree);
cout<<endl;
cout<<"不为1的节点数量"<<c<<endl;
cout<<"树的高度"<<GetHeight(tree)<<endl;
}