
回溯法的本质是穷举。对于一个多阶段决策问题,每个阶段有多个决策,每个决策会造成一个状态,当前阶段的状态依赖上一阶段的状态。所有阶段都做出决策后得到的决策序列就是问题的一个解,最后阶段的状态是对应的解值。所有可能的解构成问题的解空间。例如n=3时的0-1背包问题的解空间,设1表示当前物品放入背包的决策,0表示不放入,解空间为{(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1)}。遍历解空间就可以找到最优值和最优解。
为了方便搜索,要把解空间组织成树的形式,即解空间树。设一个状态为一个结点,当前阶段的某个结点X由上一阶段的某个结点Y(状态)通过某个决策得出,设Y是X的父节点,则一个结点有几个决策就有几个子节点。所有的结点可以构成一棵解空间树。例如n=3时的0-1背包问题的解空间树:
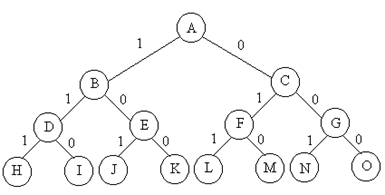
A为根节点状态值,B,C设为第一层结点,表示对第一个物品做出决策得到的状态,左节点B为第一个物品装入背包的状态(当前背包的价值),右节点C为第一个物品不装的状态。节点B,C又可以通过对决策得到下一阶段的状态节点D,E;F,G。D表示第一个物品装入时,第二个物品也装入背包的状态,G表示第一个物品不装入时第二个物品也不装入背包的状态。叶子节点的状态值分别表示问题的一个解值,获得最大值的是最优值节点。设获得最优值的叶子节点为J,对应的路径节点(A,B,E,J)构成J点的状态空间,造成这些状态的决策序列(1,0,1)就是问题的最优解。
回溯的搜索方式是深度优先的,先沿一个分支走到叶子节点,再回溯到上一节点走其他分支。比如上面的解空间树的搜索路径是A→B→D→H→D→I→D→B→E→J→E→K→E→B→A→C……→O.
约束函数:判断当前节点是否满足问题的约束条件。
显约束:对解向量中分量xi的取值限定,也就是每个阶段的决策数量。例如0-1背包问题,对每个物品只有装和不装两个选择,xi=1表示装,xi=0表示不装。
隐约束:为满足问题的解而对不同分量xi之间施加的约束,根据具体问题而定。例如0-1背包问题,要求装入背包的物品总重量不大于背包容量,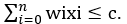
上界函数:判断当前节点的子树中有没有可能获得最优值。
方法1:在当前节点的状态下,对剩下所有阶段都做贪心决策得到的最终状态值如果不大于当前最优值,那么当前节点的子树中不可能获得最优值,可以剪枝。例如0-1背包问题,物品i选择不放入背包时,设剩下所有物品都装入背包,当前状态值加剩下所有物品价值如果不大于当前最优值则剪去当前结点的子树。
方法2:先对问题的每个阶段进行贪心排序,然后在满足隐约束的情况下,对剩下未决策的物品做贪心决策得到的最终状态如果不大于当前最优值,那么当前节点的子树中不可能获得最优值,可以剪枝。例如0-1背包问题,先把物品按单位重量的价值降序,物品i选择不放入背包时,按顺序把剩下所有物品装入背包直到装满为止,当前状态值加上剩下能装入背包的物品价值如果不大于当前最优值则剪去当前结点的子树。n比较大时,这个方法比较快。
解空间结构:子集树与排列树。
当给定的问题是从n个元素的集合S中找出满足某种性质的子集时,相应的解空间树称为子集树。例如,n个物品的0-1 背包问题所对应的解空间树是一棵子集树,该类树通常有2n个叶子结点,总结点数为2n+1- 1,遍历子集树的任何算法需要的计算时间复杂度均为O(2n)。
当给定的问题是确定 n 个元素满足某种性质的排列时,对应的解空间树称为排列树。排列树通常有n! 个叶子结点,遍历排列树需要的计算时间复杂度为O(n!)。
回溯法的求解步骤:
1、针对所给问题,定义问题的解空间;
2、确定易于搜索的解空间结构;
3、以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效索。
常用的剪枝函数:用约束函数在扩展结点处剪去不满足约束的子树;用限界函数剪去得不到最优解的子树。
【例1】装载问题:有一批共 n 个集装箱要装上 2 艘载重量分别为 c1 和 c2 的轮船,其中集装箱 i 的重量为 wi,且所有货物总重量<=c1+c2。要求确定是否有一个合理的装载方案可将这个集装箱装上这 2 艘轮船。如果有,找出一种装载方案。
首先将第一艘轮船尽可能装满,然后将剩余的集装箱装在第二艘轮船上。只需要找到尽可能把第一个轮船装满的方案就可获得最优值和最优解,相当于只考虑重量的0-1背包问题。为了简化设n=3。设1表示当前集装箱装入1船,0表示不装。解空间:{(1, 1, 1), (1, 1, 0), (0, 1, 0), (1, 0, 1), (1, 0, 0), (0, 1, 1), (0, 0, 1), (0, 0, 0)}。解空间结构为子集树。
解空间树:


1 import java.util.Arrays;
2 import java.util.Stack;
3 public class Backtrack {
4 private static int n = 5;//集装箱数量
5 private static int[] w = {0,15,10,25,15,30} ;//各个集装箱重量,数组下标表示物品编号,忽略下标0的元素。
6 private static int c1 = 50;//第一艘船的载重量
7 private static int c2 = 50;//第二艘船的载重量
8 private static int c1w = 0;//记录当前装入第一艘船的集装箱重量
9 private static int c2w = 0;//记录当前装入第二艘船的集装箱重量
10 private static int best1w = 0; //最终装入第一艘船的集装箱重量(最优值)
11 private static int best2w = 0; //最终装入第二艘船的集装箱重量
12 private static Stack<Integer> c1x = new Stack<>();//记录当前装入第一艘船的集装箱代号
13 private static Stack<Integer> best1x = new Stack<>(); //最终装入第一艘船的集装箱代号(最优解)
14 private static Stack<Integer> c2x = new Stack<>();//记录当前装入第一艘船的集装箱代号
15 private static Stack<Integer> best2x = new Stack<>(); //最终装入第二艘船的集装箱代号
16 private static long s,e;//算法计时
17 public static void main(String[] args) {
18 s=System.nanoTime();//回溯开始时间
19 backtrack(1);//回溯法遍历解空间树
20 e=System.nanoTime();//回溯结束时间
21 int[] w1 = Arrays.copyOfRange(w,1,6);//消去0下标元素,方便打印
22 System.out.println("各个集装箱的重量:"+ Arrays.toString(w1));
23 System.out.println("第一艘船载重量是:"+c1+" ; "+"第二艘船载重量是:"+c2+" ;");
24 System.out.println("装入第一艘船的集装箱重量是:"+best1w);
25 System.out.println("装入第一艘船的集装箱编号是:"+best1x);
26 System.out.println("装入第二艘船的集装箱重量是:"+best2w);
27 System.out.println("装入第二艘船的集装箱编号是:"+best2x);
28 System.out.println("遍历解空间树用时:"+(e-s)+"纳秒");
29 }
30 private static void backtrack (int i) { /*回溯搜索空间树,每一层结点表示对一个集装箱的选择,搜索第i层结点,就是选择当前集装箱i装入第几艘船。本题思路是先尽可能装满第一艘船,剩余的集装箱再装第二艘船,只需考虑第一艘船的最优装载就好了,因此左右子树的判断条件都以第一艘船为准。若当前集装箱i装第一艘船,则i+1就是i节点的左子树根节点。若当前集装箱i不装入第一艘船就装入第二艘船,则i+1就是i节点的右子树根节点。*/
31 if (i > n) { //到达叶结点为递归终止条件
32 if (c1w > best1w) {// 更新最优值和最优解
33 best1w = c1w;
34 best2w = c2w;
35 best1x = (Stack<Integer>)c1x.clone();
36 best2x = (Stack<Integer>)c2x.clone();
37 }
38 return;
39 }
40 if (w[i] <= c1 - c1w) { //如果i集装箱重量不大于第一艘船剩余载重量就进入左子树
41 c1x.push(i);//集装箱i装入第一艘船
42 c1w += w[i];//更新第一艘船当前载重量
43 backtrack(i + 1);//递归搜索左子树
44 c1x.pop();//左子树搜索完就回溯到上一节点准备搜索右子树。
45 c1w -= w[i];
46 }
47 if (upperBound(i + 1) > best1w) {/*先计算右子树根节点的上界,
48 如果其上界函数值>当前的最优值best1w,右子树中就可能存在第一艘船的装载最优解,则进入右子树。*/
49 c2x.push(i);//集装箱i不装入第一艘船就装入第二艘船。
50 c2w += w[i];//更新第二艘船当前重量
51 backtrack(i + 1);//递归搜索右子树
52 c2x.pop();//右子树搜索完就回溯到上一节点,发现左右子树都搜索完就继续回溯上一节点准备搜索右子树。
53 c2w -= w[i];
54 }
55 }
56 private static int upperBound(int i) {
57 int ci = c1w;//当前节点的上界值 = 当前载重量c1w + 剩余未装船集装箱的重量
58 while (i <=n ){
59 ci += w[i];
60 i++;
61 } return ci;
62 }
63
64 }
65 /*运行结果:
66 各个集装箱的重量:[15, 10, 25, 15, 30]
67 第一艘船载重量是:50 ; 第二艘船载重量是:50 ;
68 装入第一艘船的集装箱重量是:50
69 装入第一艘船的集装箱编号是:[1, 2, 3]
70 装入第二艘船的集装箱重量是:45
71 装入第二艘船的集装箱编号是:[4, 5]
72 遍历解空间树用时:68100纳秒
73 */
【例2】0-1背包:物品20件,背包容量50,物品重量1-10随机赋值,物品价值1-100随机赋值。
为了简化设n=3。设1表示当前物品装入背包,0表示不装。解空间:{(1, 1, 1), (1, 1, 0), (0, 1, 0), (1, 0, 1), (1, 0, 0), (0, 1, 1), (0, 0, 1), (0, 0, 0)}。解空间结构为子集树。
解空间树:

1 import java.util.Arrays;
2 import java.util.Random;
3 import java.util.Stack;
4 public class Backtrack {
5 private static int n = 20;//物品数量
6 private static int c = 50;//背包容量
7 private static int[] w = new int[n+1];//各个物品重量,为方便计算,数组下标从1开始使用。
8 private static int[] v = new int[n+1];//各个物品价值
9 private static double[] sortByV= new double[n+1];//单位重量的物品价值(降序)
10 private static int currentW = 0;//当前背包中物品的总重量
11 private static int currentV = 0;//当前背包中物品的总价值
12 private static int bestV = 0;//当前背包中物品的最优总价值(最优值)
13 private static Stack<Integer> currentX = new Stack<>();//当前装入背包中的物品编号
14 private static Stack<Integer> bestX = new Stack<>();//最优值时装入背包的物品编号(最优解)
15 private static long s,e;//回溯算法运行时间
16 public static void main(String[] args) {
17 Random r = new Random();
18 for (int i = 1; i <=n ; i++) {//随机赋值
19 w[i] = r.nextInt(10)+1;
20 v[i] = r.nextInt(100)+1;
21 }
22 SortByValue();//按单位重量的物品价值降序排序
23 s=System.nanoTime();//回溯开始时间
24 backtrack(1);//从第一个物品开始回溯求解
25 e=System.nanoTime();//回溯结束时间
26 System.out.println("物品数量为:"+n);
27 System.out.println("背包容量为:"+c);
28 int[] w1 = Arrays.copyOfRange(w,1,n+1);//消去0下标元素,方便打印
29 int[] v1 = Arrays.copyOfRange(v,1,n+1);
30 System.out.println("物品重量为:"+Arrays.toString(w1));
31 System.out.println("物品价值为:"+Arrays.toString(v1));
32 System.out.println("最优值为:"+bestV);
33 System.out.println("最优解为:"+bestX);
34 System.out.println("遍历解空间树用时:"+(e-s)+"(纳秒)");
35 }
36 public static void SortByValue (){//为方便计算上界函数,将物品按单位重量的价值降序排序
37 double[] temp1 = new double[n+1];//临时数组
38 double[] temp2 = new double[n+1];
39 int[] temp3 = Arrays.copyOf(w,w.length);
40 int[] temp4 = Arrays.copyOf(v,v.length);
41 for (int i = 1; i <=n ; i++) {
42 temp1[i]=(double) v[i]/w[i];//获得单位重量物品的价值,强制转换成浮点数。
43 temp2[i]=(double) v[i]/w[i];
44 }
45 Arrays.sort(temp1);//升序
46 int a =n;//数组下标最大值
47 for (int i = 1; i <=n ; i++) {
48 sortByV[i]=temp1[a];a--;//降序
49 }
50 //同步给w[]v[]排序,保持物品编号统一。
51 for (int i = 1; i <=n ; i++) {//遍历sortByV[]
52 for (int j = 1; j <=n ; j++) {//遍历temp2[]
53 if (sortByV[i]==temp2[j]){//按sortByV[]的顺序寻找i物品原来的编号
54 w[i]=temp3[j];v[i]=temp4[j];/*按i物品原来的编号找到对应物品的重量和价值把w[] v[]重新排序,使其编号对应的物品与sortByV[]一样*/
55 }
56 }
57 }
58 }
59 private static int upperBound(int i) {/*上界函数值=当前节点的背包价值currentV +背包剩余容量c-currentW能装下的最大价值(只能装剩下未选过的物品)*/
60 int ci = c - currentW; //当前节点的背包剩余容量
61 int cvi = currentV;//当前节点的背包总价值
62 // 把剩下未选过的物品以单位重量价值递减序装入背包
63 while (i <= n && w[i] <= ci) {
64 ci -= w[i];
65 cvi += v[i];
66 i++;
67 }
68 // 最后一个装不下的物品按重量比例计算价值,完全装满背包。
69 if (i <= n) cvi += v[i] / w[i] * ci;//
70 return cvi;
71 }
72 private static void backtrack (int i) { /*回溯搜索空间树,一层结点表示对一个物品的选择,搜索第 i 层结点,选择当前物品是否放入。若当前物品i放入背包,则i+1就是i节点的左子树根节点。若当前物品i不放入背包,则i+1就是i节点的右子树根节点。*/
73 if (i > n) { // 到达叶结点为递归终止条件
74 if (currentV > bestV) {//更新最优值和最优解
75 bestV = currentV;
76 bestX = (Stack<Integer>)currentX.clone();
77 }
78 return;
79 }
80 if (w[i] <= c-currentW) { //如果当前物品i的重量不大于背包剩余容量,则放入背包,进入左子树。
81 currentX.push(i);//物品i装入背包
82 currentV += v[i];//更新当前背包的总重量和总价值。
83 currentW += w[i];
84 backtrack(i + 1);//递归搜索左子树
85 currentX.pop();//左子树搜索完就回溯到上一节点准备搜索右子树。
86 currentW -= w[i];
87 currentV -= v[i];
88 }
89 if (upperBound(i + 1) > bestV){ /* 先计算右子树根节点的上界,
90 如果其上界函数值>当前的最优值bestV,右子树中就可能存在最优解,则进入右子树。*/
91 backtrack(i + 1); //递归搜索右子树
92 }
93 }
94 }
95 /*物品数量为:20
96 背包容量为:50
97 物品重量为:[1, 2, 3, 6, 7, 5, 7, 5, 5, 2, 9, 7, 2, 5, 1, 3, 3, 8, 9, 9]
98 物品价值为:[47, 83, 70, 98, 93, 66, 92, 63, 58, 22, 82, 59, 15, 37, 6, 15, 15, 18, 10, 9]
99 最优值为:752
100 最优解为:[1, 2, 3, 4, 5, 6, 7, 8, 9, 11]
101 遍历解空间树用时:68300(纳秒)*/
【例3】旅行售货员问题:某售货员要到若干城市去推销商品,一直各城市之间的路程,他要选定一条从驻地出发,经过每个城市一遍,最后回到住地的路线,使总的路程最短。
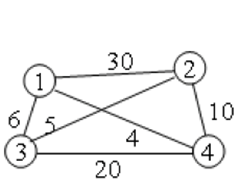
解空间:{(1,2,3,4),(1,2,4,3),(1,3,2,4),(1,3,4,2),(1,4,2,3),(1,4,3,2)}。解空间结构为排列树。
解空间树:

搜索到叶子节点加上返回1的路程才是最终状态值。

1 import java.util.Stack;
2 public class Backtrack {
3 private static int n = 4;//城市数量
4 private static int starCity = 1;//开始的城市
5 private static int[][] map = new int[n+1][n+1];//地图数据
6 private static boolean[] citybool = new boolean[n+1];//确定走过的城市
7 private static int currentS =0;//记录当前路程
8 private static int bestS =Integer.MAX_VALUE;//全部走完后的最短路程(最优值)
9 private static Stack<Integer> currentX = new Stack<Integer>();//记录当前路径
10 private static Stack<Integer> bestX = new Stack<Integer>();//最优值时的路径(最优解)
11 private static long s,e;//记录回溯算法运行时间
12 public static void main(String[] args) {
13 //地图数据初始化
14 map[1][2] = 30;map[1][3] = 6; map[1][4] = 4;
15 map[2][1] = 30;map[2][3] = 5; map[2][4] = 10;
16 map[3][1] = 6; map[3][2] = 5; map[3][4] = 20;
17 map[4][1] = 4; map[4][2] = 10;map[4][3] = 20;
18 currentX.push(starCity);//开始城市入栈
19 citybool[starCity]=true;//开始城市确定已走过
20 s=System.nanoTime();//回溯开始时间
21 backtrack(starCity);//开始回溯求解
22 e=System.nanoTime();//回溯结束时间
23 System.out.println("最优值是:"+bestS);
24 System.out.println("最优解是:"+bestX);
25 System.out.println("遍历解空间树用时:"+(e-s)+"纳秒");
26 }
27 private static void backtrack(int cityNode) {//回溯搜索空间树
28 if (currentX.size() == n) {//每个城市都走过了,准备返回开始城市。
29 if (map[currentX.peek()][starCity] != 0) {//判断最后到达的城市是否能直接返回开始城市
30 currentS += map[currentX.peek()][starCity];//记录当前路程
31 currentX.push(starCity);//记录途径点
32 if (currentS < bestS) {//更新最优值和最优解
33 bestS = currentS;
34 bestX = (Stack<Integer>) currentX.clone();
35 }
36 currentX.pop();//回溯复原
37 currentS -= map[currentX.peek()][starCity];
38 }
39 return;
40 }
41 for (int i = 1; i <= n; i++) {
42 if (map[cityNode][i] != 0 && !citybool[i]) {//如果存在当前城市直达i城的路且没走去过i城就去i城
43 currentS += map[cityNode][i];//记录开始城市到i城的路程
44 citybool[i] = true;//确定i城走过
45 currentX.push(i);//记录途径点
46 if (currentS < bestS) {//剪枝
47 backtrack(i); }//递归遍历i节点的子树
48 currentS -= map[cityNode][i];//回溯复原
49 citybool[i] = false;
50 currentX.pop();
51 }
52 }
53 }
54 }
55 /*最优值是:25
56 最优解是:[1, 3, 2, 4, 1]
57 遍历解空间树用时:92800纳秒*/
【例4】批处理作业调度:给定 n 个作业的集合{J1, J2, …, Jn}。每个作业必须先由机器 1 处理,然后由机器 2 处理。作业 Ji 需要机器 j 的处理时间为 tji。对于一个确定的作业调度,设 Fji 是作业 i 在机器 j 上完成处理的时间。所有作业在机器 2 上完成处理的时间和称为该作业调度的完成时间和。批处理作业调度问题要求对于给定的 n 个作业,制定最佳作业调度方案,使其完成时间和达到最小。
实例:作业1--作业2--作业3的加工顺序需要多少时间?
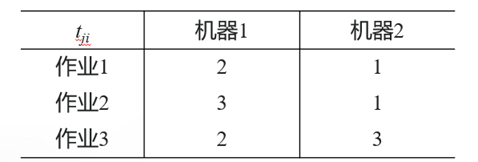
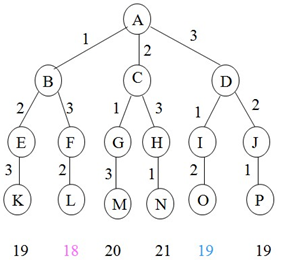
解空间:{(1,2,3),(1,3,2),(2,1,3),(2,3,1),(2,1,3),(3,1,2),(3,2,1)}。解空间结构为排列树。
解空间树:

1 import java.util.Stack;
2 public class Backtrack {
3 private static int n =3;//作业数
4 private static int[][] machiningT = {{0,0},{2,1},{3,1},{2,3}};//每个作业的在1,2机器上的加工时长
5 private static boolean[] arranged = new boolean[n+1];//确定安排过的作业
6 private static int[] f1 = new int[n+1];//当前调度下每个作业在机器1上完成处理的时间
7 private static int[] f2 = new int[n+1];//当前调度下每个作业在机器2上完成处理的时间
8 private static int currentFtS = 0;//当前调度下所有作业的完成时间和
9 private static int optimalFtS = Integer.MAX_VALUE;//最优调度时所有作业的完成时间和
10 private static Stack<Integer> currentSS = new Stack<>();//当前作业调度方案
11 private static Stack<Integer> optimalSS = new Stack<>();//最优调度方案
12 public static void main(String[] args) {
13 backtrack(1);
14 System.out.println("最小时间和为:"+optimalFtS);
15 System.out.println("最优调度方案为:"+optimalSS);
16 }
17 private static void backtrack(int i){
18 if (i>n){//到达叶结点为递归终止条件
19 if (currentFtS < optimalFtS){//更新最优值和最优解
20 optimalFtS = currentFtS;
21 optimalSS = (Stack<Integer>) currentSS.clone();
22 }
23 return;
24 }
25 for (int j = 1; j <= n; j++) {
26 if (!arranged[j]){
27 f1[i] = f1[i-1] + machiningT[j][0];
28 if (i==1){
29 f2[i] = f1[i] + machiningT[j][1];
30 }else {
31 f2[i] = (Math.max(f2[i - 1] , f1[i]) + machiningT[j][1]);
32 }
33 currentFtS += f2[i];
34 arranged[j] = true;
35 currentSS.push(j);
36 if (currentFtS < optimalFtS){//剪枝
37 backtrack(i+1);
38 }
39 currentFtS -= f2[i];
40 f2[i] = 0;
41 f1[i] = 0;
42 arranged[j] = false;
43 currentSS.pop();
44 }
45 }
46 }
47 }/*最小时间和为:18
48 最优调度方案为:[1, 3, 2]*/
【例5】n 后问题:在 n×n 格的棋盘上放置彼此不受攻击的 n 个皇后。按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n 后问题等价于在 n× n 格的棋盘上放置 n 个皇后,任何 2 个皇后不放在同一行或同一列或同一斜线上。

解空间:1-8的全排列。
解空间树:1-8的全排列树。
这个解空间非常大,列不完,总之不用想太复杂,按找1-8的排列树搜索,不符合条件的剪枝,八个皇后都符合条件就记一种方案。

1 public class Backtrack {
2 //棋盘边长
3 private static int n = 8;
4 //临时记录一种方案,确保不冲突
5 private static int[] x = new int[n+1];
6 //方案数
7 private static int scheme = 0;
8 private static void backtrack (int t) {
9 //搜索第 t 层子树,每层子树表示在第t列的皇后
10 if (t > n){
11 //到达叶子结点,方案增加1。
12 scheme++;
13 return;
14 }
15 for (int i = 1; i <= n; i++) {
16 //确定在第t列的皇后的行号i
17 x[t] = i;
18 //判断当前皇后在i行是否会与前面的皇后冲突
19 if (feasibility(t)) {
20 //不冲突则递归搜索下一列的皇后
21 backtrack(t + 1);
22 }
23 //回溯过程省略了,因为下一层自动刷新x[t]的值。
24 }
25 }
26 private static boolean feasibility(int j) {
27 //当前皇后与之前选的皇后不能处于同一正、反对角线。
28 for (int k = 1; k < j; k++) {
29 if ((Math.abs(j - k) == Math.abs(x[k] - x[j])) || (x[k] == x[j])) {
30 return false;
31 }
32 }
33 return true;
34 }
35 public static void main(String[] args) {
36 backtrack(1);
37 System.out.println("方案数为:"+scheme);
38 }
39 }/*方案数为:92*/
【例6】图的 m 着色问题:
图的 m 可着色判定问题:给定无向连通图 G = (E, V)和m 种不同的颜色。用这 m 种颜色为图 G 的各顶点着色,每个顶点着一种颜色。是否有一种着色法使 G 中每条边的 2 个顶点着不同颜色。这个问题是图的 m 可着色判定问题。
图的 m 可着色优化问题:若一个图最少需要 m 种颜色才能使图 G 中每条边连接的 2 个顶点着不同颜色,则称这个数 m 为该图的色数。求一个图的色数 m 的问题称为图的 m 可着色优化问题。
实例:n=6,m=3;邻接矩阵:

为了简化,设顶点有3个,颜色有2种,1和0分别表示一种颜色。解空间:{(1, 1, 1), (1, 1, 0), (0, 1, 0), (1, 0, 1), (1, 0, 0), (0, 1, 1), (0, 0, 1), (0, 0, 0)}。解空间结构为子集树。
解空间树:

我不是懒得画图,我只是为了方便对比。多一种颜色(m++),每个结点就多一个子结点,多一个顶点(n++)就多一层结点。遍历子集树,每一层表示一个顶点的状态,根据邻接矩阵判断任意两个相连的顶点如果是同一种颜色就剪枝,如果每个顶点都成功着色就记一种方案。

1 public class Backtrack {
2 //结点数
3 private static int n = 6;
4 //颜色数
5 private static int m = 3;
6 private static int[][] edge = {
7 {0,1,0,0,0,1},
8 {1,0,1,0,0,1},
9 {0,1,0,1,1,0},
10 {0,0,1,0,1,0},
11 {0,0,1,1,0,1},
12 {1,1,0,0,1,0}
13 };//记录方案数
14 private static int scheme = 0;
15 //临时记录一种方案,确保不冲突
16 private static int[] x = new int[n];
17 public static void main(String[] args) {
18 backtrack(0);
19 System.out.println("方案数为:"+scheme);
20 }
21 private static void backtrack(int t){
22 //到达叶子节点
23 if (t == n){
24 scheme++;
25 return;
26 }//遍历每种颜色
27 for (int i = 1; i <= m; i++) {
28 //给当前顶点着i色
29 x[t] = i;
30 //如果当前顶点与之前着色的顶点不冲突
31 if (feasibility(t)) {
32 //递归下一顶点
33 backtrack(t+1);
34 } //回溯过程省略了,因为下一层自动刷新x[t]的值。
35 }
36 }
37 private static boolean feasibility( int j){
38 for (int k = 0; k < n; k++) {
39 if (edge[j][k] == 1 && x[j]!=x[k]) {
40 return true;
41 }
42 }
43 return false;
44 }
45 }/*方案数为:380*/

用二维数组表示地图,围墙是1,走过的也是1,能走的是0,每次有3个方向的选择(有一个方向是上一步),只要下一步能走就走,递归下一步。这是一个子集树,每个节点有最多3个子节点,层数未知,反正有路就走,直到到达终点,对比当前路径是否是最短路径,是的话就更新地图。

1 public class Demo11 {
2 private static int n = 8;//结点数
3 private static int shortest = Integer.MAX_VALUE;//确定方案
4 private static Stack<Integer[]> a = new Stack<>();
5 private static Stack<Integer[]> b = new Stack<>();
6 private static int[][] maze = {
7 {1,1,1,1,1,1,1,1,1,1},
8 {1,0,0,0,1,0,0,0,0,1},
9 {1,0,0,0,1,0,1,0,0,1},
10 {1,0,1,1,1,0,1,0,0,1},
11 {1,0,0,0,0,0,1,0,0,1},
12 {1,1,1,1,1,1,1,0,0,1},
13 {1,0,0,0,0,0,0,0,0,1},
14 {1,0,0,1,1,1,1,1,1,1},
15 {1,0,0,0,0,0,0,0,0,1},
16 {1,1,1,1,1,1,1,1,1,1}
17 };
18 public static void main(String[] args) {
19 backtrack(1,1);
20 System.out.println("最短路径为:");
21 for (int i = 0; i < b.size(); i++) {
22 Integer[] step =b.get(i);
23 maze[step[0]][step[1]]=i+1;
24 if (i==b.size()-1){
25 System.out.println(Arrays.toString(step));
26 }else if ((i+1)%5==0){
27 System.out.println(Arrays.toString(step)+"-->");
28 }else {
29 System.out.print(Arrays.toString(step)+"-->");
30 }
31 }
32 System.out.println("在迷宫中表示为:");
33 for (int i = 0; i < 10; i++) {
34 for (int j = 0; j < 10; j++) {
35 if (j==9){
36 if (maze[i][j]>=10) {
37 System.out.println(maze[i][j]+" ");
38 }else {
39 System.out.println(" "+maze[i][j]+" ");
40 }
41 }else {
42 if (maze[i][j]>=10){
43 System.out.print(maze[i][j]+" ");
44 }else {
45 System.out.print(" "+maze[i][j]+" ");
46 }
47 }
48 }
49 }
50 }
51 private static void backtrack(int i, int j){
52 maze[i][j]= 1;
53 a.add(new Integer[]{i,j});
54 if (i == n && j == n){//到达出口
55 if (a.size()<shortest){
56 b = (Stack<Integer[]>)a.clone();
57 }
58 return;
59 }
60 if (maze[i+1][j] == 0) {
61 backtrack(i+1,j);
62 }
63 if (maze[i][j+1] == 0) {
64 backtrack(i,j+1);
65 }
66 if (maze[i-1][j] == 0) {
67 backtrack(i-1,j);
68 }
69 if (maze[i][j-1] == 0) {
70 backtrack(i,j-1);
71 }
72 maze[i][j]=0;//回溯复原
73 a.pop();
74 }
75 }


