区间动态规划
合并果子
有n对石子,可以选择相邻的两堆,付出的代价的是两堆石子之和,把n堆石子合并到一堆最小的代价是多少。
f[l][r] 表示第l到第r堆合并到一起需要的体力值。
for(int i = 1;i <= n; i++)
f[i][i] = 0;
for(int len = 2;len <= n; len++){
for(int l = 1,r = len;r <= n; l++,r++){
for(int k = l;k < r; k++){
f[l][r] = min(f[l][r],f[l][k] + f[k+1][r] + sum[l~r])
}
}
}
环形合并石子
环形里面总有一条边是用不上的,从那个边断开成链,再按上面的做。枚举断点。或者做双倍DP。
括号匹配
POJ2955
给出一个的只有()[]四种括号组成的字符串,求最多能够选出多少个括号满足完全匹配。
f[l][r]表示从l到r的答案。
f[i][j] = f[i][k] + f[k+1][j] +
再加一个什么?这个不像之前做过的题,要把所有跨区间的加上,比如下面的:
以上的操作只需要通过正确枚举区间断点即可解决,真正需要特别考虑的是一下的情况:
这里我们只需要特别考虑区间左右端点上面的括号匹配就可以。因为枚举断点的时候分开的区间都不能为空,所以这是需要且只需要考虑的情况。
删数字
POJ1651
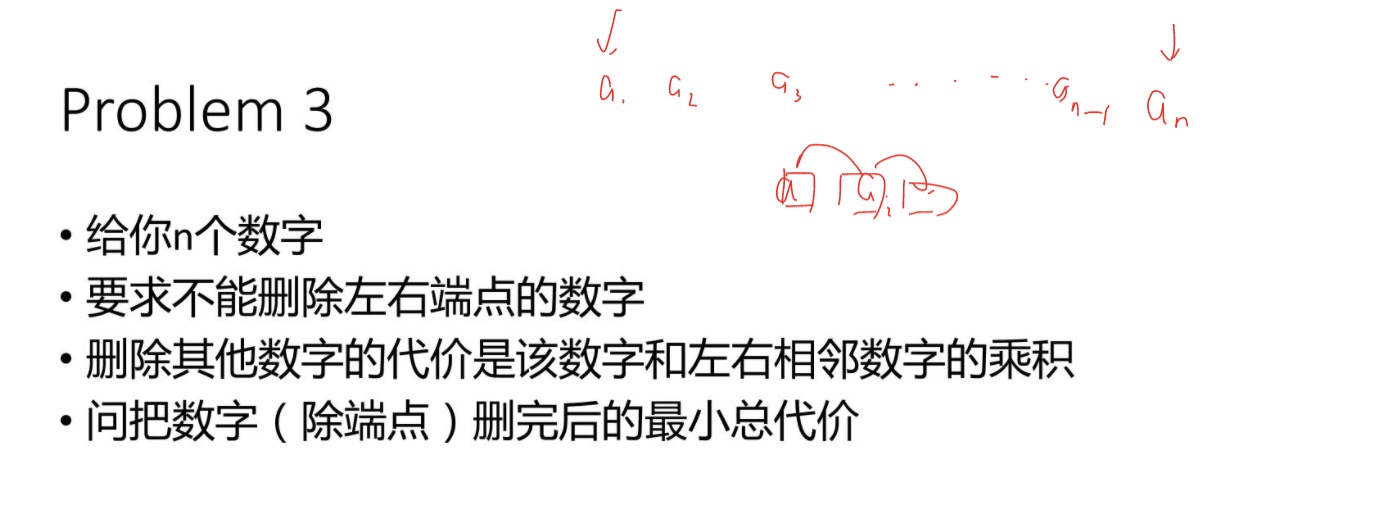
f[l][r] = f[l][k] + f[k][r] + a[l] * a[k] * a[r]
回文子序列
给定字符串,求回文子序列的数量。
f[l][r]表示l到r的数量。要避免算重算漏两种情况。
没话说 牛逼
多边形
给定凸四边形,每个点有一个权值,将多边形三角化,每个三角形的三个点权乘起来在求和,求最小和。
f[l][r]。如果连两个不能构成三角形的端点,就相当于把区间分成了左右两部分。则状态转移:
背包
(背包九讲赶紧去看嗷嗷嗷嗷嗷)
基础问题
n个物品,m容量的包,,每个物品有体积和价值,最大化价值和。
1:可以使用无限次
就是01背包的扩展,体现在代码上就是正着枚举
2:可以使用有限次
①:01背包 f[i] = max(f[i],f[i-v[j]] + w[j])
f[0][0] = 0;
for(int i = 1;i <= n; i++){
for(int j = 0;j <= m; j++){
f[i][j] = f[i-1][j];
if(j > v[i]) f[i][j] = max(f[i][j],f[i-1][j-v[i]] + w[i]);
}
}
for(int i = 0;i < n; i++){
for(int j = 0;j <= m; j++){
f[i+1][j] = max(f[i+1][j],f[i][j]);
f[i+1][j+v[i+1]] = max(f[i+1][j+v[i+1]],f[i][j] + w[i]);
}
}
一维写法:
for(int i = 1;i <= n; i++)
for(int j = m;j >= v[i];j--)
f[j] = max(f[j],f[j-v[i]] + w[i]);
- 求最大价值的具体方案
pre[i][j]:假设是从f[i-1][k]转移到f[i][j]的,假如转换完之后体积总量没发生变化,就相当于没选,如果发生变化就是已经选了。
有限背包
第一种方法:f[i][j][k]表示i种物品j的体积用了k个
第二种方法:转化成01背包。
空间复杂度:(M imes sum k)(M是体积),但是还是三次方。接下来看怎么降维优化。首先想到二进制拆分,把k进行二进制拆分,也就是把第j中物品的k件拆成2进制,不直接放入k个w[j]和v[j],而是放入((w[j],v[j])、(2 imes w[j],2 imes v[j])、2^2 imes(w[j],v[j])……2^{log _2 k} (w[j],v[j]))。
代码
v_[i],w_[i],k[i];//当前的背包
v[i],w[i];//原来的01背包
for(int i = 1;i <= n; i++){
int r = 1;
while(r <= k[i]>){
cnt++;
v[cnt] = v_[i] * r;
w[cnt] = w_[i] * r;
r <<= 1;
k[i] -= r;
}
if(k[i] != 0){
cnt++;
v[cnt] = v_[i] * k[i];
w[cnt] = w_[i] * k[i];
}
}
多次询问删数
k组询问,每次询问(p_i)表示删除第(p_i)种背包之后的01背包问题。注意:每个询问相互独立。
(n <= 10^5,M <= 100,k <= 1000)
正着DP一遍,前i个物品的情况,倒着DP一遍,后i个物品的情况。
f[][]//正着
g[][]//倒着
for(int i = 1;i <= q; i++){
cin >> k;
for(int j = 0;j <= v[k]; j++){
ans = max(ans,f[i-1][j] + f[i+1][v[k] - j]);//v是体积
}
}