#QBXT2020 3月DP营 Day1上午

QBXT DP精讲

DP的实质是图论。

状态对对应节点，转移对应边

DP的三要素是 状态、转移、初始化。

斐波那契数列：

用其他状态计算这个状态。

f[0] = 0,f[1] = 1;
for(int i = 2;i <= n; i++) 
    f[i] = f[i-1] + f[i-2];

用这个状态计算其他状态。

f[0] = 0,f[1] = 1;
for(int i = 0;i <= n; i++){
    f[i+1] += f[i];
    f[i+2] += f[i];
}

有的题只能用以上两种方法当中的某一种，所以全部都要掌握。

甚至还有反人类的dfs用法。

int dfs(iny n){
    if(n == 0) return 0;
    if(n == 1) return 1;
    return dfs(n-1) + dfs(n-2);
}

因为代码里面的数字只有0、1，所以f(x)就一定是f(x)个1加起来，复杂度就是O(f(x))，大概等于(2^n)

记忆化搜索

int dfs(int n){
    if(n == 0) return 0;
    if(n == 1) return 1;
    if(g[n]) return f[n];
    f[n] = dfs(n-1) + dfs(n-2);
    g[n] = 1;
    return f[n];
}

• 特征方程法

假设数组(f_n = f_{n-1} + f_{n-2})，求通项公式。

我们可以对应假设(x^2 = x + 1),解得x的值，x就是系数，得到方程(a_n = y x_1^n + z x_2^n)，把a[0],a[1]代入就好。

组合数

杨辉三角

for(int i = 0;i <= n; i++){
    c[i][0] = 1;
    for(int j = 1;j <= i; j++)
        c[i][j] = c[i-1][j-1] + c[i-1][j];
}

for(int i = 0;i <= n; i++){
    c[i][0] = 1;
    for(int j = 1;j <= i; j++){
        c[i+1][j] += c[i][j];
        c[i+1][j+1] += c[i][j];
    }
}

路径方案数

N*M的方格图，只能向右或者向下，走到右下的方案数？走到右下的最小代价？

[f[i][j] = f[i][j-1] + f[i-1][j] ]

也就是上面的杨辉三角（组合数）

[C_{n+m}^n ]

数字三角形

[f[i][j] = max(f[i-1][j-1],f[i-1][j]) + a[i][j]; ]

数字三角形2

要求路径上的数模100最大。

用之前的方法会破坏最优子结构。

重要技巧：题目没多一个条件，状态就多加一个维度。

由之前的f[i][j]变成f[i][j][k]，表示走到(i,j)的和模100是否等于k。

转移：

for(int i = 1;i <= n; i++){
    for(int j = 1;j <= n; j++){
        for(int k = 0;k < 100; k++){
            if(f[i][j][k]){
                f[i+1][j][(k+a[i+1][j])%100] = 1;
                f[i+1][j+1][(k+a[i+1][j+1])%100] = 1;
            }
        }
    }
}

（方法是用自己转移别人）

最长上升子序列 (LIS longest increasing subsequence)

这个名字好牛逼

第一种，时间复杂度为(O(n^2))

for(int i = 1;i <= n; i++){
    f[i] = 1;
    for(int j = 1;j <= j; j++){
        if(a[j] < a[i]){
            f[i] = max(f[i],f[j]+1);
        }
    }
}

memset(f,1,sizeof f);
for(int i = 1;i <= n; i++){
    for(int j = i+1;j <= n; j++){
        if(a[j] > a[i]){
            f[j] = max(f[j],f[i]+1);
        }
    }
}

第二问：求方案数，输出方案

再开一个数组，g[i]表示方案数，pre类似链表结构表示i的上一个数

for(int i = 1;i <= n; i++){
    f[i] = 1;
    g[i] = 1;
    pre[i] = 0;
    for(int j = 1;j <= j; j++){
        if(a[j] < a[i]){
            // f[i] = max(f[i],f[j]+1);
            int l = f[j] + 1;
            if(l > f[i]) f[i] = l,g[i] = 0,pre[i] = j;
            if(l == f[i]) g[i] += g[j];
        }
    }
}

memset(f,1,sizeof f);
memset(g,1,sizeof g);
for(int i = 1;i <= n; i++){
    for(int j = i+1;j <= n; j++){
        if(a[j] > a[i]){
            // f[j] = max(f[j],f[i]+1);
            int l = f[i] + 1;
            if(l > f[j]) f[j] = l,g[j] = 0,pre[j] = i;
            if(l == f[j]) g[j] += g[i];
        }
    }
}

输出

do{
    z[cnt++] = p;
    p = pre[p];
}while(p);
reverse(z + 1,c + cnt + 1);// 翻转
print;

第二种：线段树

定义一个线段树 1 - m,m = max(a1,12,a3,……an)。把a[j]的位置存储f[a[j]]，每次寻找的时候查询max(1,a[i]-1)就可以。以为是从前往后的运算，所以不会产生后面小的数算到前面的问题。

第三种：二分

若存在(p_1 < p_2),且(a_{p_1} > a_{p_2},f_{p_1} < f_{p_2}),则(a_{p_1})就失去了意义，就可以删掉。

怎么找到这样的数呢？

对于数组a，如果只要存在上述的数，就把(p_1)去掉，用(p_2)替换。那么最终的数组一定满足：z[x]表示f[a[i]] = x的最大的a[i]。、

代码：z数组表示上面那一行的a[i]的位置。

cnt = 0;
for(int i = 1;i <= n; i++){
    f[i] = 1;
    for(int j = 1;j <= cnt; j++){
        if(a[z[j]] < a[i]) f[i] = max(f[i],j+1);

        if(f[i] > cnt) cnt++,z[cnt] = i;
        else{
            if(a[i] < a[z[f[i]]]) z[f[i]] = i;
        }
    }
}

滑雪

N行M列的图，每个格子有高度，可以滑向周围四个比自己矮的格子，最远能滑多远。

记忆化搜索

f[i][j] = max(f[x][y]) + 1,(x,y)与(1,j)的曼哈顿距离为1。

DP（降维到LIS）

①把所有点的高度从小到大排序，根据规定，滑雪方向在数组里一定是从左向右滑，考虑做从左向右DP。

到f[i],查找左边所有临近的最大值，进行DP。

关键：确定DP顺序。先把无需数列变成有序数列。然后再做。

出现拓扑排序的题很可能用DP

憨八龟

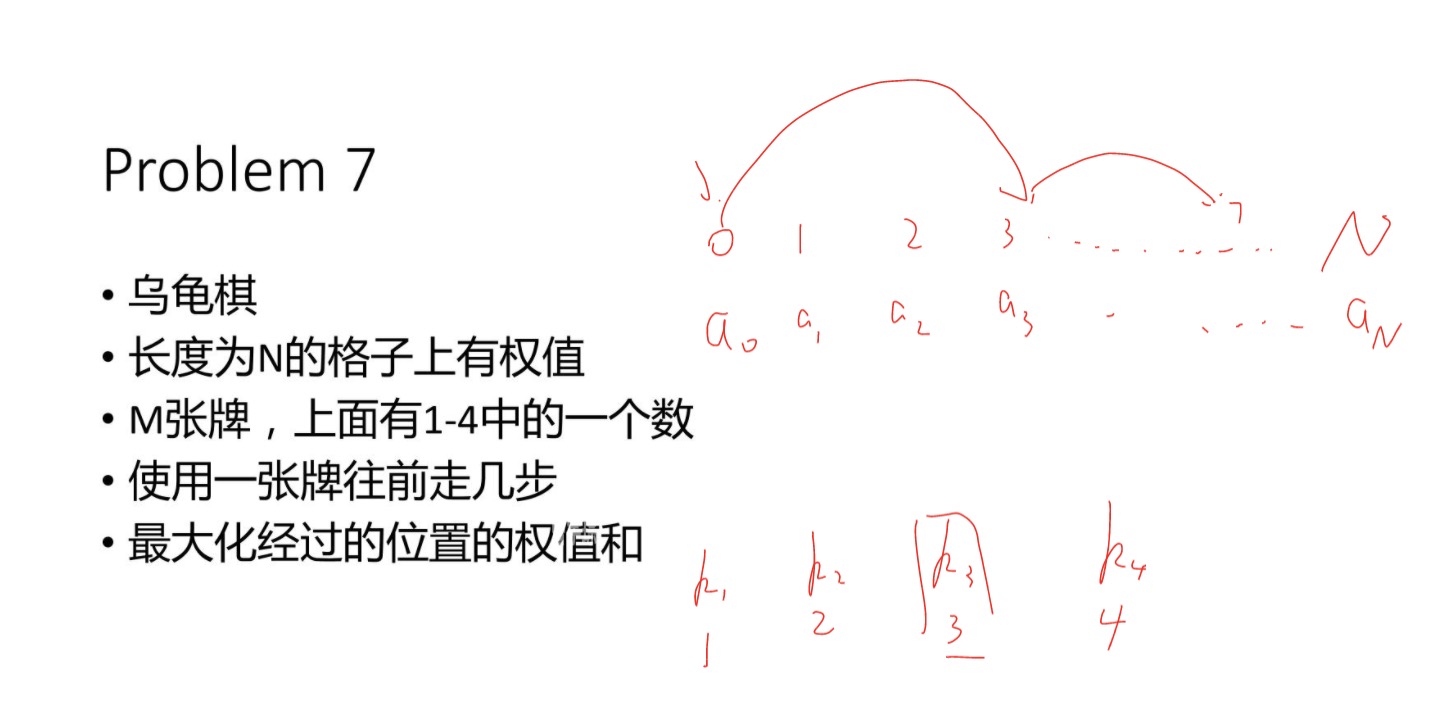
每张牌的数量是有限制的。变化的量作为状态的维度。

用一个i表示我们调到哪里了，以及用了几张各种样式的牌(a1,a2,a3,a4)。暴力定出来状态是(f[i][a1][a2][a3][a4][a5])。

我们可以知道五维的四个数有的关系a1 + 2a2 + 3a3 + 4a4 = i，这样就降成了四维的DP。

重点：冗余变量的去除。

优化