马氏距离计算一个点到一个参考分布的距离。马氏距离的优点是不受各个维度特征尺度的影响(尺度无关)。
d2 = mahal(Y, X)
d2 = mahal(Y,X)Y to the reference samples in X.
返回Y中每个点相对于参考分布X的马氏平方距离。即Y_i与分布p(mu, cov)的距离,这里mu, cov通过X进行估计。
The Mahalanobis distance is a measure between a sample point and a distribution.
The Mahalanobis distance from a vector y to a distribution with mean μ and covariance Σ is
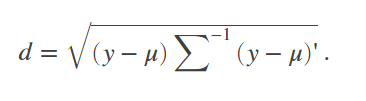
This distance represents how far y is from the mean in number of standard deviations.
mahal returns the squared Mahalanobis distance d2 from an observation in Y to the reference samples in X. In the mahal function, μ and Σ are the sample mean and covariance of the reference samples, respectively.

因此,计算一个向量中各点(或向量)到自身分布的马氏平方距离表示为:
d2 = mahal(X, X)
计算一个向量中各点(或向量)到另一个参考分布的马氏平方距离表示为:
d2 = mahal(Y, X)