归并排序

归并排序

什么是Merge（归并/合并）？

归并：把两个或多个已经有序的序列合并成一个

首先先定义一个更大的数组

接下来可以分别设定指针指向数组的第一个元素

再来就是把指向合并的散装数组里的元素进行对比。。谁小谁进大数组

只剩下一个子表未合并时，可以将该表中剩余元素全部加到总表

“2路”归并

把两个或多个已经有序的序列合并成一个

“2路”归并——每选出一个小的元素需对比关键字1次

“4路”归并

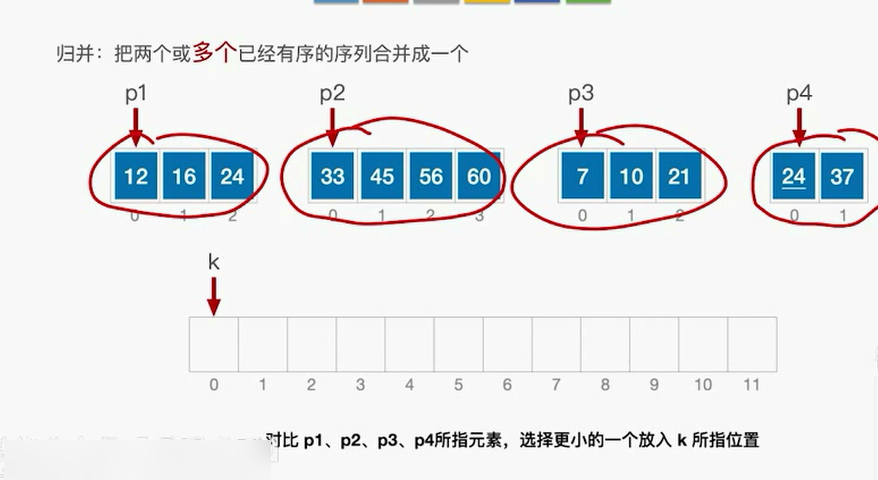
每选出一个小的元素需要对比关键字3次。

结论：m路归并，每选出一个元素需要对比关键字m-1次

归并排序（手算模拟）

在内部排序中一般采用2路归并

第一躺的归并排序，把相邻的两个部分分别进行2路归并

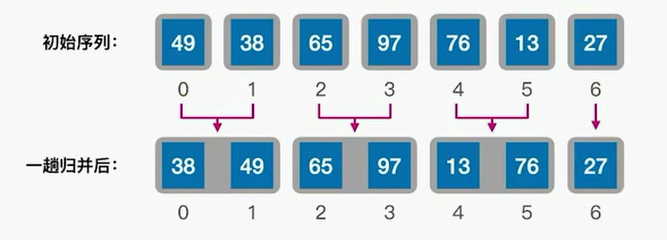
第二趟，在对上一趟的归并进行2路归并

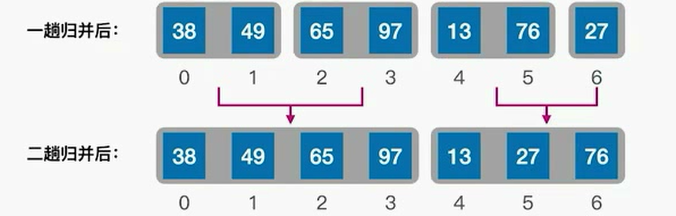
第三趟就可以得到了

13，27，38，49，65，76，97

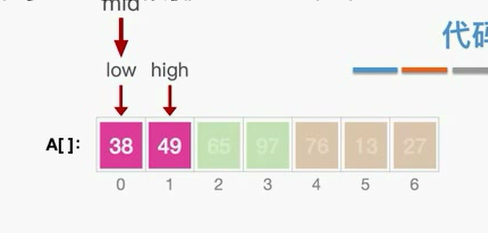
核心操作：把数组内的两个有序序列归并为一个

代码实现

int *B = (int *)malloc(n*sizeof(int));	//辅助数组B

//A[low...mid]和A[mid+1...high]各自有序，将两个部分归并
void Merge(int A[],int low,int mid,int high){
    int i,j,k;
    for(k=low;k<=high;k++)
        B[k] = A[k];					//将A中所有元素复制到B中
    for(i=low,j=mid+1,k=i;i<=mid&&j<=high;k++){
        if(B[i]<=B[j])
            A[k]=B[i++];				//将较小值复制到A中
        else
            A[k]=B[j++];
    }
    while(i<=mid)	A[k++]=B[i++];
    while(j<=high)	A[k++]=B[j++];
}

void MergeSort(int A[],int low,int high){
    if(low<high){
        int mid = (low+high)/2;
        MergeSort(A,low,mid);
        MergeSort(A,mid+1,high);
        Merge(A,low,mid,high); 
    }
}

算法效率分析

2路归并的“归并树”——形态上就是一棵倒立的二叉树

[二叉树的第h层最多有2^{h-1}个结点 ]

[若树高为h，则应满足nle2^{h-1} ]

[即h-1=lceil log_2n ceil ]

[结论：n个元素进行2路归并排序，归并趟数=lceil log_2n ceil ]

[每趟归并时间复杂度为O(n),则算法时间复杂度为O(nlog_2n) ]

[空间复杂度=O(n),来自辅助数组B ]

归并算法是稳定的。自己操作。

知识回顾