P3372 【模板】线段树 1
这个题目相对我们平时做的简单的线段树的题目(区间加,求最值)而言,这里是(区间加,求和),所以父亲节点延迟标记下传的时候父亲节点的值的增量要乘上孩子数,因为求最值的情况,整个区间同加最值不会改变。
t[id].s += (t[id].right - t[id].left + 1) * t[id].lazy;//更新节点的值
题目描述
如题,已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数加上x
2.求出某区间每一个数的和
输入输出格式
输入格式:
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输出格式:
输出包含若干行整数,即为所有操作2的结果。
输入输出样例
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=8,M<=10
对于70%的数据:N<=1000,M<=10000
对于100%的数据:N<=100000,M<=100000
(数据已经过加强^_^,保证在int64/long long数据范围内)
样例说明:
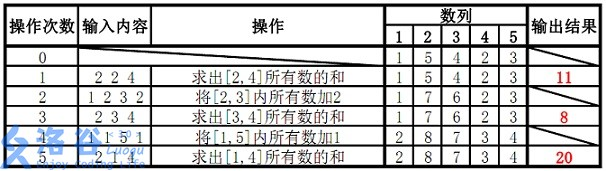
这个题目线段树的模板题,因为这里是求和,所以每个节点里面记录的是所包含的孩子的和。
因为不是求最值,所以在传递延迟标记的时候延迟标记里面的值和节点记录的孩子的和不一样。
因为我们从每个节点里面可以知道孩子数目,所以segTree[root].sum+=(segTree[root].r-segTree[root].l+1)孩子数目 *segTree[root].addMark;

1 #include <bits/stdc++.h> 2 #define ll long long 3 using namespace std; 4 ll n, m; 5 ll L = 1, a[100100]; 6 struct st_n//SegmentTree node 线段树节点 7 { 8 ll left, right;//每个节点的控制范围 9 ll lazy, s; //s表示和 10 }t[300005]; 11 void build_tree()//建线段树 12 { 13 while(L < n) L *= 2; 14 for(ll i = 1; i <= n; i++) 15 t[i + L - 1].left = t[i + L - 1].right = i, 16 t[i + L - 1].s = a[i];//将最后一层赋值 17 for(ll i = L + n;i < 2 * L;i++) 18 t[i].left = t[i].right = i - L + 1; 19 for(ll i = L - 1; i >= 1; i--) 20 t[i].left = t[2 * i].left, 21 t[i].right = t[2 * i + 1].right, 22 t[i].s += t[2 * i + 1].s + t[2 * i].s; 23 //建树 24 } 25 26 void push(ll id)//发放lazy值给左右子 27 { 28 t[2 * id].lazy += t[id].lazy;//左子 29 t[2 * id + 1].lazy += t[id].lazy;//右子 30 t[id].s += (t[id].right - t[id].left + 1) * t[id].lazy;//更新节点的值 31 t[id].lazy = 0; 32 } 33 34 //区间修改 35 void change(ll id, ll left, ll right, ll d) 36 { 37 if(t[id].left == left && t[id].right == right)//找到了 38 { 39 t[id].lazy += d; 40 return ; 41 } 42 push(id);//发放lazy值 43 if(t[2 * id].right >= right) change(2 * id, left, right, d);//如果左子的右管辖范围比所求大,则只在左子中继续change 44 else if(t[2 * id + 1].left <= left) change(2 * id + 1, left, right, d);//同上 45 else 46 { 47 change(2 * id, left, t[2 * id].right, d); 48 change(2 * id + 1, t[2 * id + 1].left, right, d); 49 //左右子分别查找 50 } 51 t[id].s = t[2 * id].s + t[2 * id + 1].s 52 + (t[2 * id].right - t[2 * id].left + 1) * t[2 * id].lazy 53 + (t[2 * id + 1].right - t[2 * id + 1].left + 1) * t[2 * id + 1].lazy; 54 //上面这步很重要,它的功能也是更新(其实我原本想写个函数) 55 } 56 ll query(ll id, ll left, ll right)//查询 57 { 58 //与change很像,就不多说了。 59 if(t[id].left == left && t[id].right == right) 60 return t[id].s + (t[id].right - t[id].left + 1) * t[id].lazy; 61 push(id); 62 if(t[2 * id].right >= right) return query(2 * id, left, right); 63 else if(t[2 * id + 1].left <= left) return query(2 * id + 1, left, right); 64 else return query(2 * id, left, t[2 * id].right) + query(2 * id + 1, t[2 * id + 1].left, right); 65 } 66 int main(int argc, char *argv[]) 67 { 68 cin >> n >> m; 69 for(ll i = 1; i <= n; i++) cin >> a[i]; 70 build_tree();//建树 71 for(ll i = 1;i <= m;i++) 72 { 73 ll p, x, y; 74 ll d; 75 cin >> p >> x >> y; 76 if(p == 1) 77 { 78 cin >> d; 79 change(1, x, y, d); 80 } 81 else 82 cout << query(1, x, y) << endl; 83 } 84 return 0; 85 }
其它代码(不正确)
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int MAXN=1e6+10; 4 int a[MAXN]; 5 struct node{ 6 int l,r; 7 int sum; 8 int addMark;//延迟标记 9 }segTree[4*MAXN]; 10 11 /* 12 建树的时候做的事情: 13 1、给左右边界,要求的值(这里是求和),以及传递标记赋初值 14 2、更新每个点表示的要求的值(这里是求和) 15 */ 16 void build(int root,int l,int r){ 17 segTree[root].l=l; 18 segTree[root].r=r; 19 segTree[root].sum=0; 20 segTree[root].addMark=0; 21 int mid=(l+r)/2; 22 if(l==r) segTree[root].sum=a[l]; 23 else{ 24 build(root*2,l,mid);//建左子树 25 build(root*2+1,mid+1,r);//建右子树 26 } 27 segTree[root].sum=segTree[root*2].sum+segTree[root*2+1].sum; 28 } 29 30 //区间更新,区间更新自然能包括单点更新 31 void update(int root,int l,int r,int add){ 32 if(segTree[root].r<l||segTree[root].l>r){//区间无关 33 return; 34 } 35 if(segTree[root].l>=l&&segTree[root].r<=r){//区间包含 36 segTree[root].addMark=add; 37 }else{//区间交叉 38 int mid=(segTree[root].l+segTree[root].r)/2; 39 //在左边子树去更新 40 if(l<=mid) update(2*root,l,r,add); 41 //在右边子树去更新 42 if(r>=mid) update(2*root+1,l,r,add); 43 } 44 segTree[root].sum=segTree[root*2].sum+segTree[root*2+1].sum; 45 } 46 47 void print(int n){ 48 cout<<"segTree[i].l"<<" "<<"segTree[i].r"<<" "<<"segTree[i].sum"<<" "<<"segTree[i].addMark"<<endl; 49 for(int i=1;i<=n;i++){ 50 cout<<segTree[i].l<<" "<<segTree[i].r<<" "<<segTree[i].sum<<" "<<segTree[i].addMark<<" "<<endl; 51 } 52 } 53 54 int main(){ 55 freopen("in.txt","r",stdin); 56 int n,m; 57 cin>>n>>m; 58 for(int i=1;i<=n;i++) cin>>a[i]; 59 build(1,1,n); 60 print(4*n); 61 for(int i=1;i<=m;i++){ 62 int op;cin>>op; 63 if(op==1){ 64 int x,y,k; 65 cin>>x>>y>>k; 66 update(1,x,y,k); 67 }else{ 68 int x,y; 69 cin>>x>>y; 70 // query(1,x,y); 71 } 72 } 73 print(4*n); 74 return 0; 75 }