OI中坑点总结

以下是我个人OI生涯中遇到的坑点的一个小总结，可能是我太菜了，总是掉坑里，请大佬勿喷

1，多重背包的转移的循环顺序

//默认每个物品体积为一（不想打码……）
//dp[i]表示占用背包容量i所能获得的最大价值
for(int i=1;i<=n;i++)
    for(int j=sum;j>0;j--)        //sum表示背包最大容量
        for(int k=0;k<=num;k++)    //num表示这个物品的数量，k表示选取当前物品k件
            if(j>=k)
                dp[j]=min(dp[j],dp[j-k]+value);

简单的多重背包模板，对于学过的人，大概清晰易懂吧

//dp[i]表示占用背包容量i所能获得的最大价值
for(int i=1;i<=n;i++)
    for(int k=0;k<=num;k++)    //num表示这个物品的数量，k表示选取当前物品k件
        for(int j=sum;j>k;j--)        //sum表示背包最大容量
            dp[j]=min(dp[j],dp[j-k]+value);

很相似的代码，只是改了循环顺序，但是为什么会错呢？

类比01背包的倒序转移，

考虑对于某种物品，标程中先枚举 j ，再枚举 k ，这样对于每个位置 j ，只能先于位置 j - i ，由 j - i ( i ∈ [ 0 , k ] )转移一次

而错误写法中，对于位置 j ，可以由转移过的位置 j - i 转移而来

这为什么会导致错误呢？考虑在 j 之前， j - i 已经由 j - i₁ - i₂ 转移而来，多重背包的物品是可以组合的，所以以上的转移等价于 dp[ j - i₁ - i₂ ] 直接转移到 dp[ i ] ，而我们不能保证 i₁ + i₂ <= num ，即可能会取多于物品总数的物品

举个例子：

物品数量为7，我们枚举位置13，由8转移而来，而在此之前，位置8由4转移而来，等价于位置13由位置4转移而来，13-4=9>7，转移非法

2，对拍fc玄学错误

因为样例普遍太水，对拍就成为了信息学竞赛中的经典调试手段

其中对比标准答案与你的程序的答案时，常用到fc，就是文件比较

考场上建议写对拍程序用system来回跑直到出错，再把错误数据拎出来用cmd跑，因为cmd会告诉你所有不一样的地方

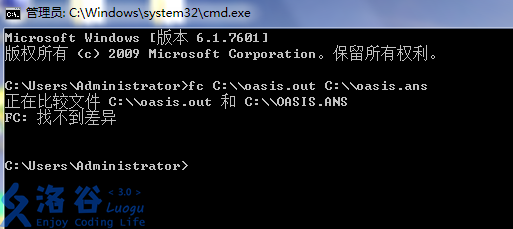
但是有时候会遇到这样的问题：

人眼看都一样，文件比较就是不一样

在怀疑程序写崩开始乱改之前，不如看看是不是遇到了下面几种情况

（1）先看看这个

这是换行符的问题，你的程序可能比标程的答案差几个换行符，不多解释，考虑到这种问题的可能就好

（2）还有这个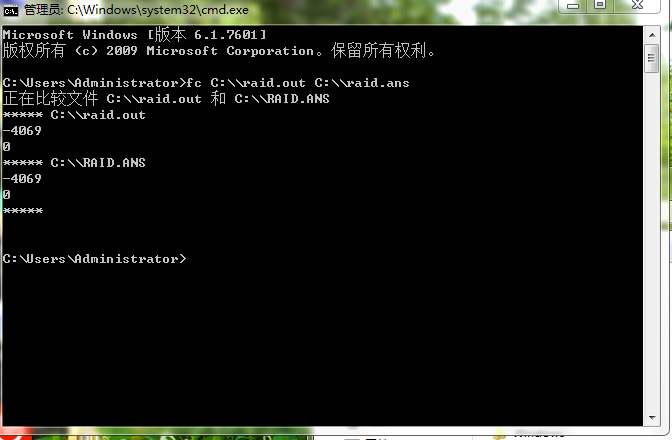



这个甚至拿出来看都一样，有心人还会发现错误总在输出结尾，但是看到程序结尾一模一样，其实这是行末空格的问题(╯°Д°)╯︵┻━┻……

3，矩阵压缩重复

矩阵压缩？？？好啦，其实我也不知道叫什么了，所以给它起了这个名字(*/ω*)

大意就是，如果给你一个矩阵n<=50000,m<=50000，开数组显然是开不下的，如果再给一个条件n*m<=500000呢，普通的二维数组还是布星，所以我们使用vector使用一维数组

把矩阵的一个位置转到一维数组上

我喜欢这么转，对于n行m列的矩阵，位于第i行第j列的元素的pos=(i-1)*m+j

这样就把矩阵上的每个位置转为1~n*m的

但是前提是你不会使用位置0，如果你使用了位置0还用这个映射

那么你会发现，本行第一个元素和上一行的最后一个元素pos值相等（在线出锅）

所以就要用pos=(i-1)*(m+1)+j了

同理，使用第0行就是pos=i*(m  or  m+1)+j

ps:我在这出锅倒是没有调太久，但是还是因为这个WA了好几次水题呢

4，树的直径合并

来看一个小题：给两棵树，我们可以在两棵树上任意两点之间连边，使这两棵树合并为一棵新树，求新树的最小直径

学过树的直径的同学都知道，len_newtree=(len_tree1+1)/2+(len_tree2+1)/2+1

式子没错，但是拿不到分，为什么呢

考虑其中一棵树的直径远大于另一棵，

所以我们知道了，完整的式子应该是这样的

len_newtree=max(max(len_tree1,len_tree2),(len_tree1+1)/2+(len_tree2+1)/2+1)

5，开数组

1，离散化数组

2，记得树状数组开数组是按值域开的

这样就一定要考虑开到极值

有这么一种情况，比如这个题，[SCOI2014]方伯伯的玉米田，我们树状数组的第二维是按高度开的，1<=a_i<=5000，但是我们在运行过程中有把玉米拔高这么一种情况，有效的值域范围应为a_i+k<=5500

6，如何避免低级错误

啊啊啊，这个东西这么好用，太好用了啊啊啊

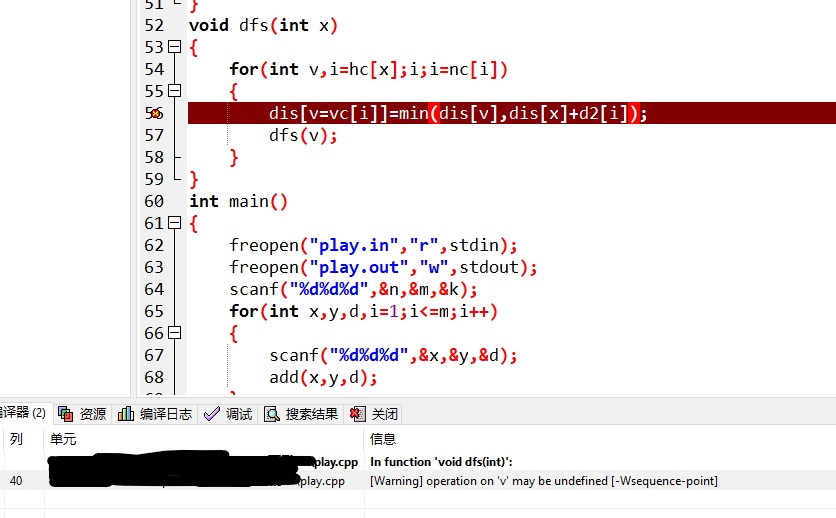
dis[v=vc[i]]=min(dis[v],dis[x]+d2[i]);

看这行代码

是一个普通的dfs过程，但是错了

这个就涉及到运算优先级的问题了，因为它是从右向左算的

然后算到dis[v]的时候，v还没有赋值

v=vc[i];
dis[v]=min(dis[v],dis[x]+d2[i]);

这么写就对了

但是这种错是很难查的啊，怎么办呢？

其实我们可以在编译时解决这个问题：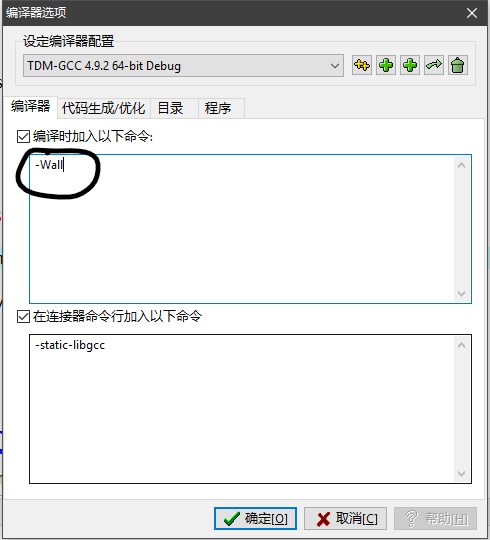



这是个好东西，它可以在你代码里面找到可能的错误，以警告的形式提出来