
今天终于完成了机器人轨迹规划的最后一次课了,拜拜自带B - BOX 的 Prof. TJ Taylor.
最后一节课的内容是利用势场来进行轨迹规划。此方法的思路非常清晰,针对Configration Space 里面的障碍物进行 DT变换,用DT变换值作为罚函数的输入,让机器人尽可能的远离障碍物,同时再终点设计抛物面函数,让机器人有向终点靠近的趋势。最后所获得的就是机器人的一种可行运动轨迹。由于此轨迹是梯度下降的,并且罚函数是连续的,所以如果机器人不陷入局部最优,那么就可以获得全局最优路径(我本人不持这样的观点,二阶Hessian矩阵大写的不服,凭什么贪婪算法是最短路径?)
1、基于DT变换生成罚函数图
DT变换是2D2值图像中的一种算法,其作用是找到某像素到最近非0像素的距离。换言之,就是机器人到最近障碍物的距离。这种距离再机器人学运动中非常容易获得,只要有实时的距离传感器,就能够找到机器人再不同位置下,到最近障碍物的距离。从而生成 f - map (罚函数图)
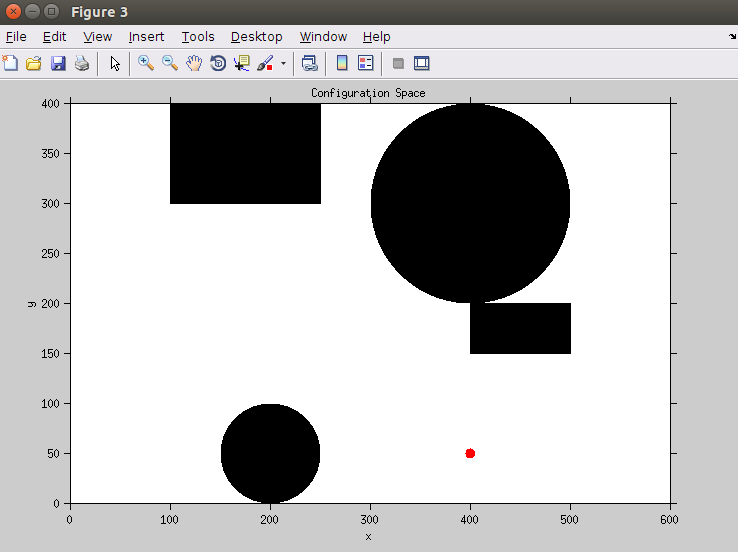
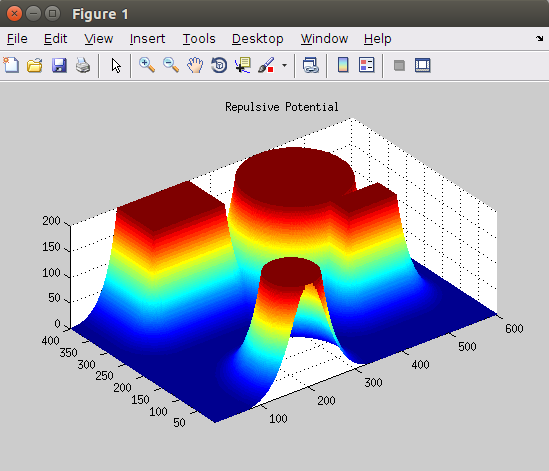
机器人的Configuration Space 与 f - map 如上图所示。
2、拉向终点的势
除了罚函数以外,机器人还需要一个拉向终点的势 —— Configuration Space 上一个以终点为中心的抛物面。将其与f - map 相加后,即可得到最终的Artificial Potential.
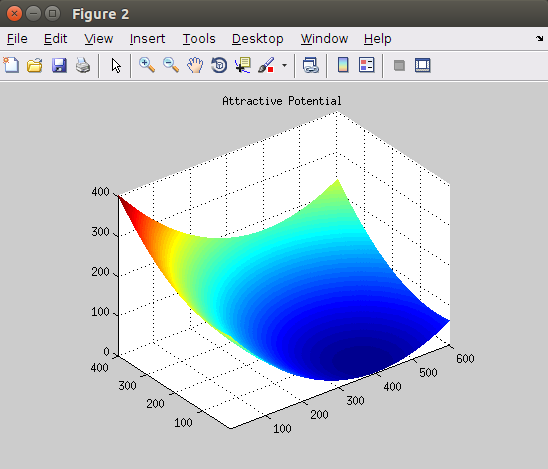
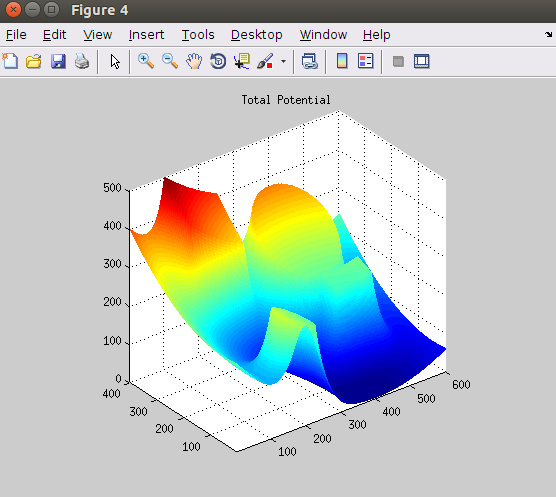
3、梯度下降
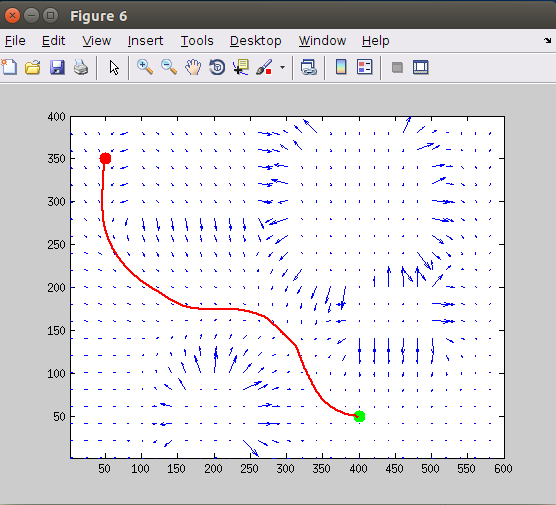
在Artificial Potential 上执行梯度下降算法,获得机器人运动轨迹。
4、总结
机器人轨迹规划是很有前景的学科,以后有前途的方向包括以下:
非同性机器人:无人汽车不能随时倒车
动力学约束下的规划:考虑机器人的加速减速
多机器人轨迹规划
针对移动障碍轨迹规划
针对不确定环境轨迹规划