[数学学习与代码]最小二乘法--多元线性方程求解

   　　最近看了一本线性代数，如下图这个样的。。。比较讨厌的是这本书的排版贼难受，定义和定理加粗基本和没加一样，排版也过于紧密，看起来一度想弃书。

 

　　重点不在这里，哈哈哈哈。

这几天看完线代后，有一个粗略的理解后，菜虽然菜，但我还是想要倒腾倒腾。想起之前学过的最小二乘法，不过是一个二阶的最小二乘法，也撸了代码。但是学过线代后总是抑制不住体内的洪荒。。。（上个厕所去）

　　N阶线性方程如下：

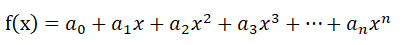
         然后根据线性方程的最小二乘法来进行计算，首先写出损失函数，设有一个样本容量为k的样本，使用n阶函数(共有n+1个系数)去拟合，损失函数为L(x_i)。

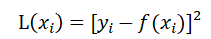
　　解释下：使用样本中的数值y_i减去理论数值f(x_i)所获得的差的平方。这样就能获得样本与理论的差的平方，我们的目的是想让每个差值可能的最小，也就是理论函数越接近样本。

　　现在需要把所有的样本都进行该处理，并将所有的L(x_i)进行求和处理获得L函数。

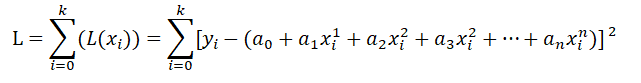
　　那么接下来讨论目标，目标是为了尽可能使L最小，那么在函数中取得最小值应该是导数为0的位置，而这里是多元函数，那么我们需要进行偏导处理。

在此，我们先确定未知量与已知量，这里y_i和x_i是作为已知量，而a_0, a_1,a₂.......a_n是作为未知量。

　　那么开始求偏导（注意数学基础，复合函数求偏导）：

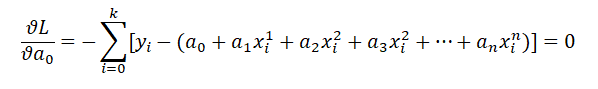
         好的，相信大家已经找出了规律来了。

　　那么通用公式是：

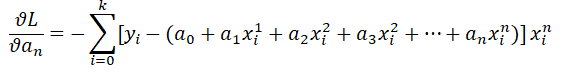
　　通共有N+1(注意n从0开始)个方程，我们再修改下方程，使其符合AX=B，注意这里A,X,B为矩阵：

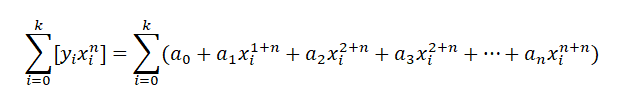
　　不妨设：

　　那么相对应的矩阵为：

　　那么接下来就是求解线性方程了！

　　要求解AX=B方程，首先，我们得对方程的系数矩阵进行处理，使其成为上三角或者下三角，比如化成上三角，那么我们可以通过最后一个数据X^′_n+1·n+1×a_n=y_ix_iⁿ,解出后进行递归处理出前面的元素：

　　在此，使用的是高斯消元法来进行处理的，但注意高斯消元法中，使用某行去消去其他行的该行对角线上元素不能为0。当然也可以使用其他的比如LU法，雅克比法。

　　最后，代码自己使用C语言打的，放最后贴出。我们取一组数据来验证下程序：

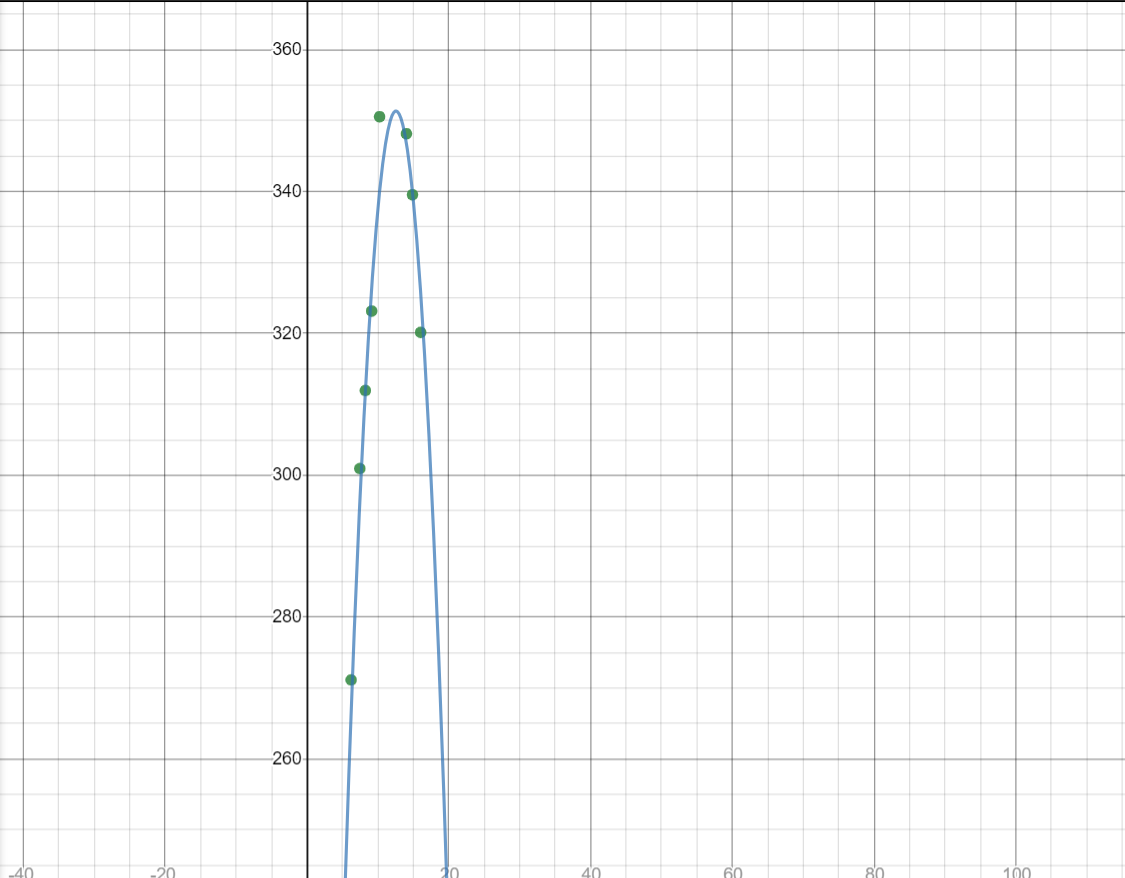
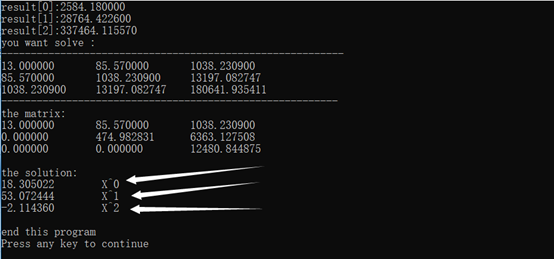
 代码下载链接：https://files.cnblogs.com/files/inkhearts/multi_least_square_method.rar