2018-03-01 20:38:34
堆(Heap)是可以用来实现优先的队列的数据结构,而不是堆栈。
- 若采用数组或者链表实现优先队列

- 若采用树的结构
如果采用二叉搜索树,那么每次删除,比如删除最大值,也就是删除最右边的叶子,那么很快这棵二叉树就不再平衡了。
那能否采用别的方法来构造树呢?
我们可以这样构造二叉树:每课树最大的元素在根处,且该定义是递归的,另外,为了保证效率,这棵树还应该是完全二叉树。
其实这就是堆的定义。
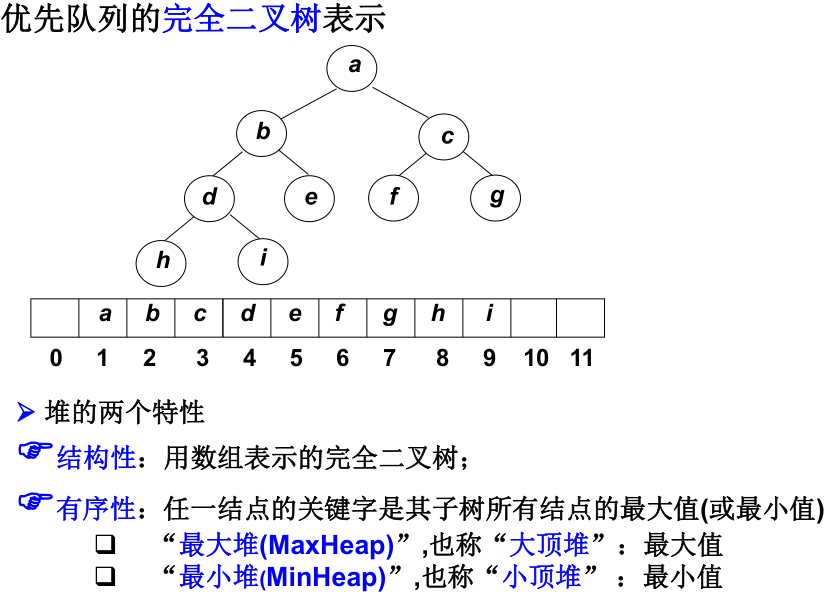
堆的抽象数据类型描述:

1)最大堆的初始化

2)堆的插入
算法描述:将插入元素放到末尾,并进行调整,将之最终插入从其父结点到根结点的有序序列中去。
时间复杂度:O(logn)

3)堆的删除
算法描述:显然为了维护完全二叉树的特点,删除的元素在末尾是比较合适的。最大堆的定义指出删除应该是删除最大值,也就是删除根结点。此时,可以采用将根结点与末尾的结点数值替换的方法,来间接的删除最大值。在末尾值移到根部之后可能会打破堆的定义,此时需要进行堆的维护。
时间复杂度:O(logn)
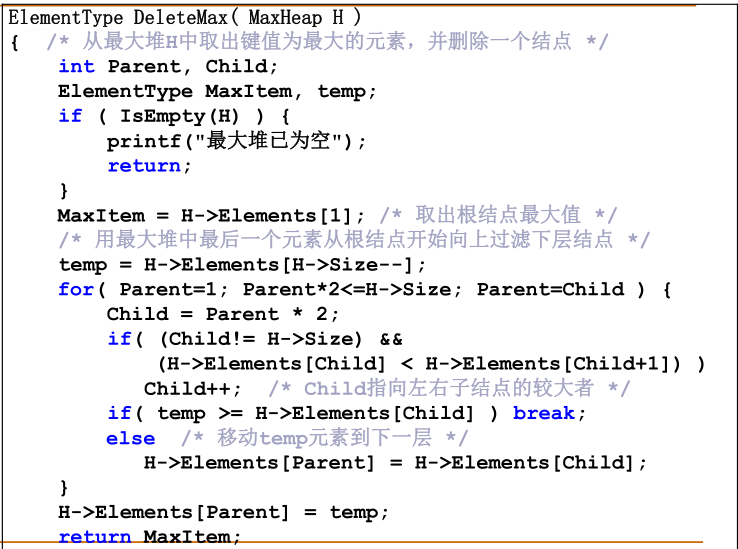
4)最大堆的建立
既然已经有了插入的算法,当然可以逐个进行插入,基于这种的算法的时间复杂是O(nlog(n))。
事实上,可以在O(n)的时间复杂度内完成建立堆,具体的思路就是首先由数组已经建立了一个完全二叉树,这时候,自底向上进行维护,这样做的目的是为了满足堆维护算法的合法性:堆的左右子树都是堆。这种算法的时间复杂度为O(n)。
