摘要:
主题模型是对文字隐含主题进行建模的方法。它克服了传统信息检索中文档相似度计算方法的缺点,并且能够在海量互联网数据中自动寻找出文字间的语义主题。主题模型在自然语言和基于文本的搜索上都起到非常大的作用。
引言:
两篇文档是否相关往往不只决定于字面上的词语重复,还取决于文字背后的语义关联。对语义关联的挖掘,可以让我们的搜索更加智能化。而主题模型则是用于解决这个方法的非常经典的模型。主题模型是对文字隐含主题进行建模的方法。它克服了传统信息检索中文档相似度计算方法的缺点,并且能够在海量互联网数据中自动寻找出文字间的语义主题。
主题模型的主要思想就是通过对文档的统计分析找到对应的主题,再有主题来找到在这个主题下会产生词语的概率。在操作中,文档和词都是已知条件而主题模型则是隐变量,基于这一点我们能够很好的利用EM算法特性。文章介绍了pLSA和LDA两种方法,通过课程能够更加实际的了解主题模型的应用。
预备知识:
一、预备概念
1、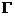 函数:
函数:
![]() 函数是阶乘在实数上的推广:
函数是阶乘在实数上的推广:


2、Beta分布
Beta分布的概率密度:
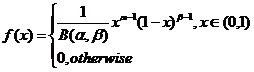
其中系数B为:
![]()
Gamma函数可以看成阶乘的实数域推广:
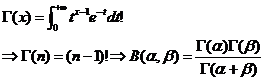
Bata分布的期望:
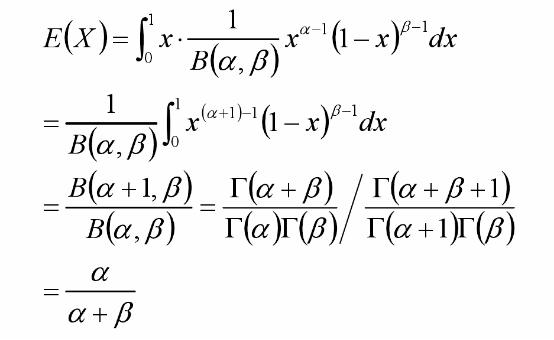
3、朴素贝叶斯的分析
朴素贝叶斯的分析可以胜任许多文本分类问题。
但是朴素贝叶斯的分析无法解决语料中一词多义和多词一义的问题——它更像是词法分析,而非语义分析。
o如果使用词向量作为文档的特征,一词多义和多词一义会造成计算文档间相似度的不准确性。
o可以通过增加“主题”的方式,一定程度的解决上述问题:
n一个词可能被映射到多个主题中o——一词多义
n多个词可能被映射到某个主题的概率很高o——多词一义
二、pLSA模型
基于概率统计的pLSA模型(probabilistic Latent Semantic Analysis,概率隐语义分析),增加了主题模型,形成简单的贝叶斯网络,可以使用EM算法学习模型参数。

PLSA模型计算方法:
D代表文档,Z代表主题(隐含类别),W代表单词;
P(di)表示文档di的出现概率,
P(zk|di)表示文档di中主题zk出现的概率,
P(wj|zk)表示给定主题zk的前提下单词wj出现的概率。
每个文档在所有主题上服从多项分布;每个主题在所有词项上服从多项分布。
整个文档的生成过程是这样的:
以P(di)的概率选中文档di;
以P(zk|di)的概率选中主题zk;
以P(wj|zk)的概率产生一个单词wj。
观察数据为(di,wj)对,主题zk是隐含变量。
(di,wj)的联合分布为:
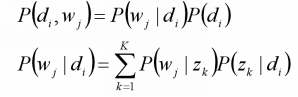
而对应了两组多项分布,而计算每个文档的主题分布,就是该模型的任务目标。
pLSA模型算法:
观察数据为(di,wj)对,主题zk是隐含变量。
目标函数(极大似然估计):
![]()
未知变量/自变量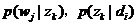
使用逐次逼近的办法:(EM算法)
假定P(zk|di)、P(wj|zk)已知,求隐含变量zk的后验概率;(E-step)
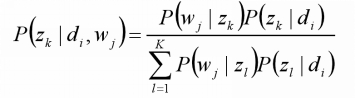
在(di,wj,zk)已知的前提下,求关于参数P(zk|di)、P(wj|zk)的似然函数期望极大值,得到最优解P(zk|di)、P(wj|zk),(M-step)
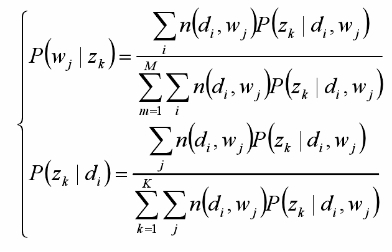
带入上一步,从而循环迭代;
PLSA模型总结
pLSA应用于信息检索、过滤、自然语言处理等领域,pLSA考虑到词分布和主题分布,使用EM算法来学习参数。
opLSA可以看做概率化的矩阵分解。
o虽然推导略显复杂,但最终公式简洁清晰,很符合直观理解;推导过程使用了EM算法,也是学习EM算法的重要素材。
二、LDA模型
pLSA不需要先验信息即可完成自学习——这是它的优势。如果在特定的要求下,需要有先验知识的影响呢?LDA模型
LDA模型:是一个三层结构的贝叶斯模型,需要超参数。
1、共轭先验分布
在贝叶斯概率理论中,如果后验概率P(θ|x)和先验概率p(θ)满足同样的分布律,那么,先验分布和后验分布被叫做共轭分布,同时,先验分布叫做似然函数的共轭先验分布。
通过共轭先验分布我们能够从 二项分布-->多项分布 Bata分布-->Dirichlet分布
2、Dirichlet分布
Bata分布:
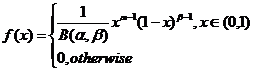
![]()
Dirichlet分布:
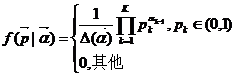
简记:
![]() ,其中:
,其中:
![]() 是参数向量,共K个
是参数向量,共K个
定义在:维上
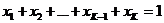
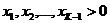
定义在(K-1)维的单纯形上,其他区域的概率密度为0
对称Dirichlet分布:
 ,其中
,其中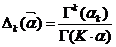
 =1时,退化为均匀分布
=1时,退化为均匀分布
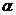 >1时,
>1时, 的概率增大
的概率增大
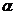 <1时,退化为均匀分布
<1时,退化为均匀分布
 >1时,的概率增大
>1时,的概率增大
3、LDA模型
LDA的解释:
共有m篇文章,一共涉及了K个主题;
每篇文章(长度为Nm)都有各自的主题分布,主题分布是多项分布,该多项分布的参数服从Dirichlet分布,该Dirichlet分布的参数为α;
每个主题都有各自的词分布,词分布为多项分布,该多项分布的参数服从Dirichlet分布,该Dirichlet分布的参数为β;
o对于某篇文章中的第n个词,首先从该文章的主题分布中采样一个主题,然后在这个主题对应的词分布中采样一个词。不断重复这个随机生成过程,直到m篇文章全部完成上述过程。
字典中共有V个term(不可重复),这些term出现在具体的文章中,就是word——在具体某文章中的word当然是有可能重复的。
语料库中共有m篇文档d1,d2…dm;
对于文档di,由Ni个word组成,可重复;
语料库中共有K个主题T1,T2…Tk;
α和β为先验分布的参数,一般事先给定:如取0.1的对称Dirichlet分布——表示在参数学习结束后,期望每个文档的主题不会十分集中。
oθ是每篇文档的主题分布
对于第i篇文档di的主题分布是θi=(θi1,θi2…,θiK),是长度为K的向量;
对于第i篇文档di,在主题分布θi下,可以确定一个具体的主题zij=k,k∈[1,K],
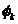 表示第k个主题的词分布,k∈[1,K],对于第k个主题Tk的词分布φk=(φk1,φk2…φkv),是长度为v的向量
表示第k个主题的词分布,k∈[1,K],对于第k个主题Tk的词分布φk=(φk1,φk2…φkv),是长度为v的向量
由zij选择φzij,表示由词分布φzij确定term,即得到观测值wij。

图中K为主题个数,M为文档总数,Nm是第m个文档的单词总数。β是每个Topic下词的多项分布的Dirichlet先验参数,α是每个文档下Topic的多项分布的Dirichlet先验参数。
zmn是第m个文档中第n个词的主题,wmn是m个文档中的第n个词。两个隐含变量θ和φ分别表示第m个文档下的Topic分布和第k个Topic下词的分布,前者是k维(k为Topic总数)向量,
后者是v维向量(v为词典中term总数)。
由于在词和文档之间加入的主题的概念,可以较好的解决一词多义和多词一义的问题。
在实践中发现,LDA用于短文档往往效果不明显——这是可以解释的:因为一个词被分配给某个主题的次数和一个主题包括的词数目尚未敛。往往需要通过其他方案“连接”成长文档。
LDA可以和其他算法相结合。首先使用LDA将长度为Ni的文档降维到K维(主题的数目),同时给出每个主题的概率(主题分布),从而可以使用if-idf继续分析或者直接作为文档的特征进入
聚类或者标签传播算法——用于社区发现等问题。