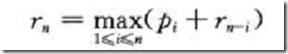本文参考《算法导论》，整理者：华科小涛@http://www.cnblogs.com/hust-ghtao/
动态规划方法通常用来求解最优化问题。
1. 基本原理
什么问题应该用动态规划方法来求解呢？
- 适合应用动态规划方法求解的最优化问题应该具备两个要素：最优子结构和重叠子问题。
-
1.1 最优子结构
-
如果一个问题的最优解包含其子问题的最优解，我们就称此问题具有最优子结构性质。使用动态规划算法时，我们用子问题的最优解来构造原问题的最优解。在动态规划方法中，我们通常自底向上的使用最优子结构。也就是说，首先求得子问题的最优解，然后求原问题的最优解。原问题最优解的代价通常是子问题最优解的代价再加上由此次选择产生的代价。
-
1.2 重叠子问题
-
适用动态规划方法求解的最优化问题应该具备的第二个性质是子问题空间必须足够小，即问题的递归算法会反复求解相同的子问题，而不是一直生成新的子问题。如果递归算法反复求解相同的子问题，我们就称最优化问题具有重叠子问题性质。动态规划算法通常这样利用重叠子问题性质：对每个子问题求解一次，将解存入一个表中，当再次需要这个子问题时直接查表，每次查表的代价为常亮时间。
-
1.3 基本步骤
我们通常按照如下4个步骤来设计一个动态规划算法：
- 刻画一个最优解的结构特征。
- 递归地定义最优解得结构特征。
- 计算最优解的值，通常采用自底向上的方法。
- 利用计算出的信息构造一个最优解。
2.钢条切割问题
题目是这样的：给定一段长度为n英寸的钢条和一个价格表pi(i=1,2,3…n)，求钢条切割方案，使得收益
最大。注意，如果长度为n英寸的钢条价格
足够大，最优解可能就是完全不需要切割。下图是一个价格表的样例：
我们将钢条从左边切割下长度为i的一段，只对右边剩下的长度为n-i的一段继续切割，对左边的一段不再进行切割。即问题的分解方式为：将长度为n的钢条分解为左边开始一段及剩余部分继续分解的结果。不做任何切割的方案：第一段为n，收益为
，剩余部分长度为0，收益
。于是得到最优解的结构特征：
2.1使用朴素递归算法
下面的过程实现了上述公式的计算，采用的是一种自顶向下的递归方法：
我们发现，如果直接将此伪代码用程序实现，一旦输入规模稍微变大，运行时间将急剧增长。原因在于CUT-ROD反复的用相同的参数值对自身进行递归调用，即它反复求解相同的子问题。下图显示n=4的情况：
为了分析CUT-ROD的运行时间，令
表示第二个参数值为n时CUT-ROD的调用次数。此值等于递归调用树中根为n的子树中的节点总数，注意此值包含了根结点对应的最初的一次调用。因此
，并且
可证明
。
2.2 使用动态规划方法
朴素递归算法之所以效率很低，是因为它反复求解相同的子问题。因此动态规划方法仔细安排求解顺序，对每个子问题只求解一次。
动态规划方法仔细安排求解顺序，对每个子问题只求解一次，并将结果保存下来。如果随后再次需要此子问题的解，只需查找保存的结果，而不必重新计算。
- 带备忘的自顶向下的方法
此方法仍按自然的递归形式编写过程，但过程中会保存每一个子问题的解。当需要一个子问题的解时，过程首先检查是否已经保存过此解。如果是，则直接返回保存的结果，从而节省了计算时间；否则按通常方式计算这个子问题。
下面是伪代码：
- 自底向上的版本
我们可以将子问题按规模从小到大进行排序，因为通常子问题只依赖于更小的子问题的求解，所以我们可以按规模由小到大的顺序依次求解。当求解某个子问题时，它所依赖的更小的子问题都已经被求解保存，所以每个子问题只需求解依次，大大提高效率。
下面是自底向上版本的代码：
通过分析可知，上述两种方法的时间复杂度为
-
重构解
前面钢条切割问题的动态规划算法返回最优解的收益值，但是并未返回解本身。下面是扩展动态规划算法，不仅保存最优收益值，还保存最优的切割方案。BOTTOM-UP-CUT-ROD的扩展版本，它对长度为j的钢条，不仅计算最大收益值
，还保存最优解对应的第一段钢条的切割长度
：
下面的过程接受两个参数：价格表
和钢条长度n，然后调用上面函数计算切割下来的每段钢条长度，最后输出长度为n的钢条的完整的切割方案：
3.总结
当问题具有最优子结构和重叠子问题时，可以考虑用动态规划算法。动态规划方法安排求解顺序，对每个子问题只求解一次，并将结果保存下来。如果随后再次需要此子问题的解，只需查找保存的结果，而不必重新计算。因此动态规划算法是付出额外的内存空间来节省计算时间，是典型的时空权衡的例子。