损失函数 (loss function )
衡量模型输出与真实的标签之间的差距
损失函数:(单样本)
Loss =f(y^,y)
y^:预测函数
y: 标签函数
代价函数:(cost function )(总体)
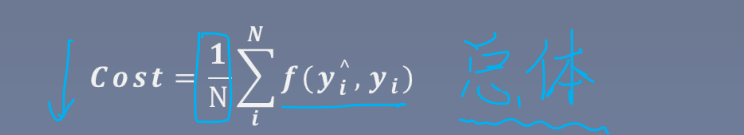
反映的是总体的平均值
目标函数(objective function):
obj= cost + Regularization Term
cost : 最小,表示模型输出与标签的差异
regular: (正则项) 最小化
让模型不要太复杂,减轻过拟合现象
【常见的两种损失函数】
1.MSE (均方误差,Mean squared Error)
输出与标签之差的平方的均值,常在回归任务中使用
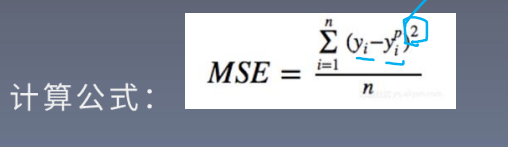

2.CE (cross Entroy ,交叉熵)
交叉熵信息论,用于衡量两个分布的差异,常在分类任务中使用。计算公式:

信息熵:描述信息的不确定度
自信息:L(x) =-logP(x) ,P(x) 是某事件发生的概率
信息熵: == 所有可能取值的信息量的期望,
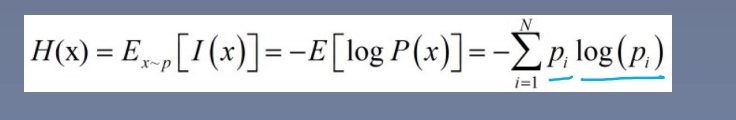
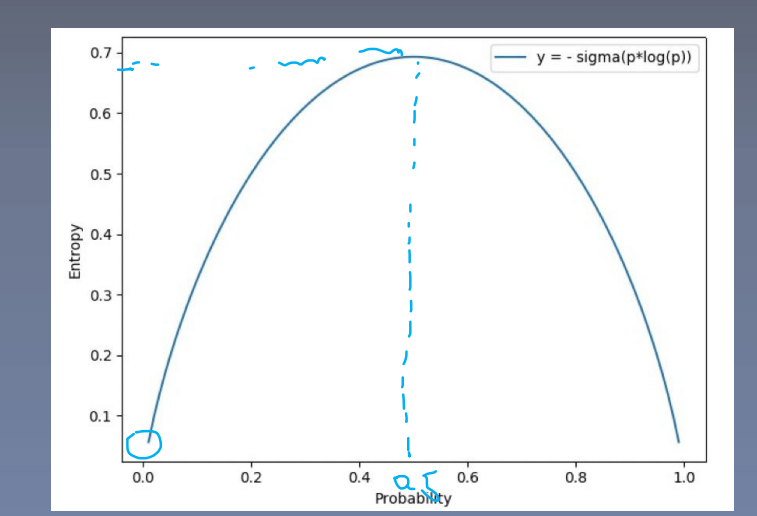
-
- 概率在0.5 的时候,熵是最大的,不确定性也是最大的
- 信息熵 越大,信息越不确定
- 信息熵越小,信息越确定
【相对熵】
又称k-L 散度,衡量两个分布之间的差异。公式如下

H(p,q)= H(P) + D_KL(P||Q),即 交叉熵 =信息熵 + 相对熵
结论: 优化交叉熵等价于优化相对熵

【交叉熵】: 衡量俩个概率分布的差异
概率有两个性质:
1.概率值是非负的
2.概率之和等于1
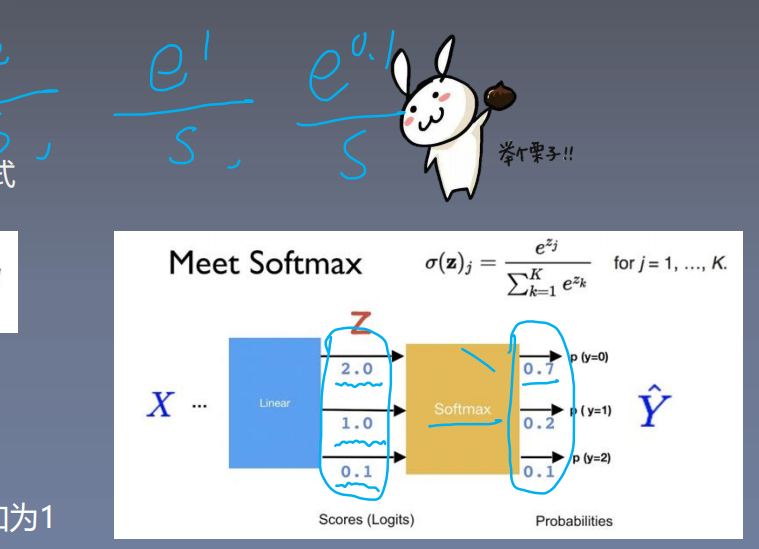
交叉熵的好伙伴---softmax 函数: 将数据变换待符合概率分布的形式
【softmax 函数】
将数据变换到符合概率分布的形式

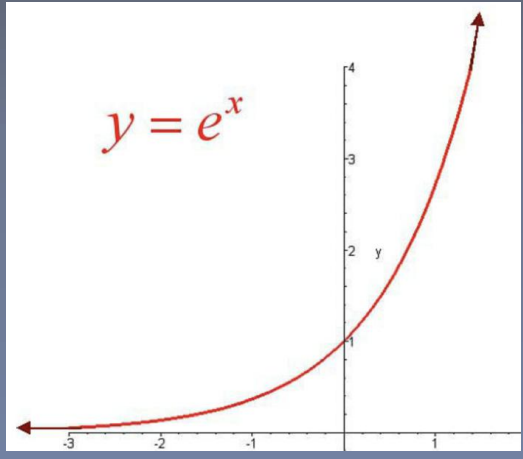
概率两性质: softmax 操作:
1.概率值是非负的 1.取指数,实现非负
2.概率之和等于1 2.除以指数之和,实现之和为1
没有一个损失函数会适合所有的任务,损失函数会涉及算法类型、求导是否容易、数据中异常值的分布问题