HDU3861The King’s Problem

                                                                      HDU3861 

    kosaraju缩点+最小路径覆盖

   为什么是最小路径覆盖呢，我们假设有一个如下DAG图

 

 

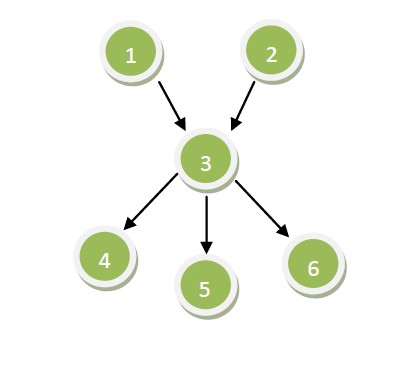
 目前我们1出发到了3处，对于3的儿子4、5、6，肯定是不能彼此到达的。所以最好的情况3只能延伸一个方向，比如4，解法

 如代码。则有1—3—4，2，5，6，答案是4条。

#include<cstdio>
#include<cstring>
#include<stack>
#include<cstdlib> 
#include<queue>
#include<memory.h>
#include<algorithm>
#include<vector>
#include<iostream>
using namespace std;
const int maxn=5010;
vector<int>G[maxn];
vector<int>G2[maxn];
vector<int>S;
vector<int>Map[maxn];
int scc[maxn],vis[maxn],n,m,scc_cnt,ans;
int link[maxn];
void _update(){
    for(int i=1;i<=n;i++) G[i].clear();
    for(int i=1;i<=n;i++) G2[i].clear();
    memset(link,0,sizeof(link));
    memset(vis,0,sizeof(vis));
    memset(scc,0,sizeof(scc));
    S.clear();
    ans=scc_cnt=0;
}
void _dfs1(int v){
    if(vis[v]) return ;
    vis[v]=1;
    int L=G[v].size();
    for(int i=0;i<L;i++)_dfs1(G[v][i]);
    S.push_back(v);
    return ;
}
void _dfs2(int v){
    if(scc[v]) return ;
    scc[v]=scc_cnt;
    int L=G2[v].size();
    for(int i=0;i<L;i++) _dfs2(G2[v][i]);
}
void _kosaraju()
{
    for(int i=1;i<=n;i++)_dfs1(i);
    for(int i=n-1;i>=0;i--) {
        if(!scc[S[i]]) {
            scc_cnt++;
            Map[scc_cnt].clear(); 
            _dfs2(S[i]);
         }
    }
    for(int i=1;i<=n;i++)
    {
        int L=G[i].size();
        for(int j=0;j<L;j++){
            if(scc[i]!=scc[G[i][j]]){
               Map[scc[i]].push_back(scc[G[i][j]]);
            }
        }
    }
} 
bool _find(int v){
    int L=Map[v].size();
    for(int i=0;i<L;i++)
    {
        if(!vis[Map[v][i]]){
            vis[Map[v][i]]=1;
            if(!link[Map[v][i]]||_find(link[Map[v][i]])){
                link[Map[v][i]]=v;
                return true;
            }
        }
    }
    return false;
}
int main()
{
    int T,i,j,u,v;
    scanf("%d",&T);
    while(T--){
        _update();
        scanf("%d%d",&n,&m);
        for(i=1;i<=m;i++){
            scanf("%d%d",&u,&v);
            G[u].push_back(v);
            G2[v].push_back(u);
        }
        _kosaraju();
        for(i=1;i<=scc_cnt;i++){
            memset(vis,0,sizeof(vis));
            if(_find(i)) {
              ans++;
            }
        }
        printf("%d
",scc_cnt-ans);//以Map图位对象，不是n 
    }
    return 0;
}