在面试时,避免不了的会遇到一些数据结构的面试题,今天我们就来了解一下二叉树的经典面试题:
已知二叉树的前序遍历顺序为ABCDEGHF,中序遍历顺序为DBAGEHCF,求该二叉树的后序遍历。
还有:
已知二叉树的中序遍历顺序为DBAGEHCF,后序遍历顺序为DBGHEFCA,求该二叉树的前序遍历。
类似的面试题应该如何应对呢?
文章持续更新,微信搜索「万猫学社第一时间阅读,关注后回复「电子书」,免费获取12本Java必读技术书籍。
什么是二叉树?
在开始之前,容我再唠叨几句:什么是二叉树?二叉树(Binary Tree)是一种特殊的树,树上的每个结点最多有两个子树的树结构,也就是说每一个父结点最多长出两个树杈。通常两个子结点被称为左子结点和右子结点。比如:
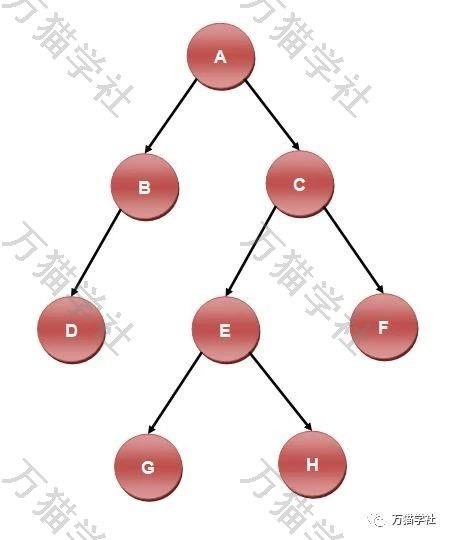
其中,A就是整个二叉树的根结点,那么B就是A的左子结点,C就是A的右子结点。每一个结点,我们可以用Java语言这样实现:
/**
* 二叉树结点
*/
public class TreeNode {
public char value;
/**
* 左子树
*/
public TreeNode left;
/**
* 右子树
*/
public TreeNode right;
}
三种遍历方式
在解题之前,先把先序遍历、中序遍历、后序遍历这三种遍历方式说清楚,为之后的解题打下良好的基础。
文章持续更新,微信搜索「万猫学社第一时间阅读,关注后回复「电子书」,免费获取12本Java必读技术书籍。
先序遍历
先序遍历就是,先访问根结点,再访问左子结点,再访问右子结点。上图二叉树的先序遍历的顺序就是ABCDEGHF。我们可以用Java语言这样实现:
public void preOrder(TreeNode biTree) {
System.out.println(biTree.value);
if(biTree.left != null) {
preOrder(biTree.left);
}
if(biTree.right != null) {
preOrder(biTree.right);
}
}
中序遍历
先序遍历就是,先访问左子结点,再访问根结点,再访问右子结点。上图二叉树的中序遍历的顺序就是DBAGEHCF。我们可以用Java语言这样实现:
public void preOrder(TreeNode biTree) {
if(biTree.left != null) {
preOrder(biTree.left);
}
System.out.println(biTree.value);
if(biTree.right != null) {
preOrder(biTree.right);
}
}
文章持续更新,微信搜索「万猫学社第一时间阅读,关注后回复「电子书」,免费获取12本Java必读技术书籍。
后序遍历
先序遍历就是,先访问左子结点,再访问右子结点,再访问根结点。上图二叉树的后序遍历的顺序就是DBGHEFCA。我们可以用Java语言这样实现:
public void preOrder(TreeNode biTree) {
if(biTree.left != null) {
preOrder(biTree.left);
}
System.out.println(biTree.value);
if(biTree.right != null) {
preOrder(biTree.right);
}
}
经过上面的叙述,可以总结出:先序遍历、中序遍历、后序遍历三种遍历中的“先”、“中”、“后”都是指根结点的访问顺序,“先”则是先访问根结点,“中”则是在左右中间访问根结点,,“后”则是最后访问根结点。
已知前中序遍历顺序,求后序遍历顺序
扯了这么多,还是回到刚刚的第一道面试题上:
已知二叉树的前序遍历顺序为ABCDEGHF,中序遍历顺序为DBAGEHCF,求该二叉树的后序遍历。
我们的解题思路是,先根据前中序遍历顺序重新构造出这个二叉树,再根据二叉树写出后序遍历顺序。
文章持续更新,微信搜索「万猫学社第一时间阅读,关注后回复「电子书」,免费获取12本Java必读技术书籍。
重构二叉树
前序遍历(ABCDEGHF)中的第一个结点A肯定为根结点,那么在中序遍历(DBAGEHCF)中,A结点的左边(DB)肯定为结点A的左子树,A结点的右边(GEHCF)肯定为结点A的右子树,初步判断二叉树是这样的:
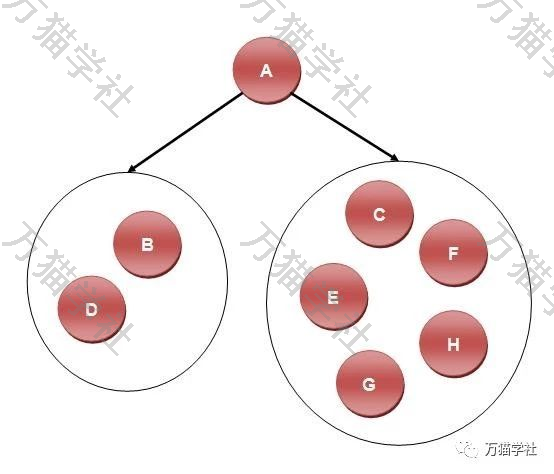
再看A的左子树(DB),在前序遍历(ABCDEGHF)中,B在最前面,说明B为该子树的根结点,再看中序遍历(DBAGEHCF),B的左边(D)肯定为A的左子树,B的右边(无)肯定为A的右子树,初步判断二叉树是这样的:
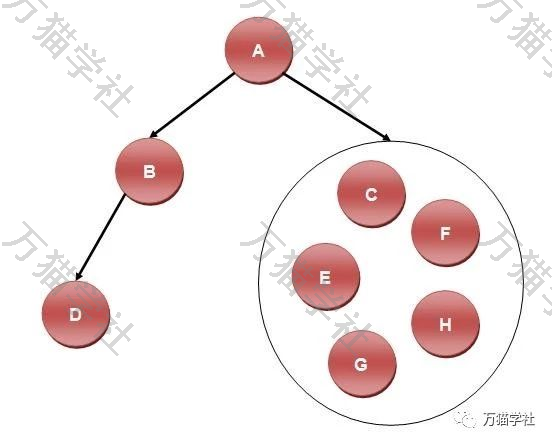
再看A的右子树(GEHCF),在前序遍历(ABCDEGHF)中,C在最前面,说明C为该子树的根结点,再看中序遍历(DBAGEHCF),C的左边(GEH)肯定为C的左子树,C的右边(F)肯定为C的右子树,初步判断二叉树是这样的:
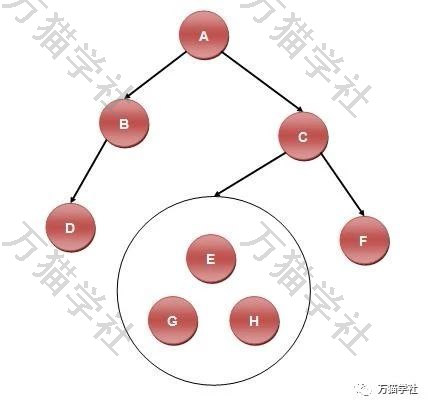
再看C的左子树(GEH),在前序遍历(ABCDEGHF)中,E在最前面,说明E为该子树的根结点,再看中序遍历(DBAGEHCF),E的左边(G)肯定为E的左子树,E的右边(H)肯定为E的右子树,可以最终判断出二叉树是这样的:

文章持续更新,微信搜索「万猫学社第一时间阅读,关注后回复「电子书」,免费获取12本Java必读技术书籍。
写出后序遍历顺序
这个步骤就比较容易了,根据二叉树得到的后序遍历顺序就是:DBGHEFCA
已知中后序遍历顺序,求前序遍历顺序
扯了这么多,还是回到刚刚的第一道面试题上:
已知二叉树的中序遍历顺序为DBAGEHCF,后序遍历顺序为DBGHEFCA,求该二叉树的前序遍历。
我们的解题思路是,先根据中后序遍历顺序重新构造出这个二叉树,再根据二叉树写出前序遍历顺序。
重构二叉树
后序遍历(DBGHEFCA)中的最后一个结点A肯定为根结点,那么在中序遍历(DBAGEHCF)中,A结点的左边(DB)肯定为结点A的左子树,A结点的右边(GEHCF)肯定为结点A的右子树,初步判断二叉树是这样的:

再看A的左子树(DB),在后序遍历(DBGHEFCA)中,B在最后面,说明B为该子树的根结点,再看中序遍历(DBAGEHCF),B的左边(D)肯定为A的左子树,B的右边(无)肯定为A的右子树,初步判断二叉树是这样的:

再看A的右子树(GEHCF),在后序遍历(DBGHEFCA)中,C在最后面,说明C为该子树的根结点,再看中序遍历(DBAGEHCF),C的左边(GEH)肯定为C的左子树,C的右边(F)肯定为C的右子树,初步判断二叉树是这样的:

再看C的左子树(GEH),在后序遍历(DBGHEFCA)中,E在最后面,说明E为该子树的根结点,再看中序遍历(DBAGEHCF),E的左边(G)肯定为E的左子树,E的右边(H)肯定为E的右子树,可以最终判断出二叉树是这样的:

文章持续更新,微信搜索「万猫学社第一时间阅读,关注后回复「电子书」,免费获取12本Java必读技术书籍。
写出后序遍历顺序
这个步骤就比较容易了,根据二叉树得到的前序遍历顺序就是:ABCDEGHF
微信公众号:万猫学社
微信扫描二维码
关注后回复「电子书」
获取12本Java必读技术书籍
