前言
工程实现的过程中需要对提取的特征指标进行有效性分析,评价各个特征指标与分类器不同类别的显著性关系,筛选出对不同类别判别贡献率最佳的指标,为设计分类器等提供支持。
本文主要针对单因子方差分析法。
实现步骤
1.方差分析法的原理;
2.数据准备;
3.单因子方差分析法的matlab实现;
4.特征的多重比较检验;
实现过程
1. 方差分析法的原理;
方差分析法(Analysis of Variance, ANOVA)又称为F检验或者变异数分析,其目的是推断两组或多组资料的总体均数是否相同,检验两个或多个样本均数的差异是否具有统计学意义。
1.1 方差齐性检验的必要性
方差分析的F检验是以各个实验组内总体方差齐性为前提的,因此,应该先要对各个实验组内的总体方差进行齐性检验。如果各个组内总体方差为齐性,而且经过F检验所得多个样本所属总体平均数差异显著,这时才可以将多个样本所属总体平均数的差异归因于各种实验处理的不同所致;如果各个组内总体方差不齐,那么经过F检验所得多个样本所属总体平均数差异显著的结果,可能有一部分归因于各个实验组内总体方差不同所致。
进行方差分析需要首先进行方差齐性检验,即若组间方差不齐则不适用方差分析,但可以通过对数变换、倒数变换等方法变换后再进行方差齐性检验,若还不行只能进行参数检验,不过一般认为,如果各组参数相若,就算未能通过方差齐性检验,问题也不大。
方差齐性检验也成为Levene检验,主要用于检验两个或多个样本之间的方差是否齐性,要求样本为随机样本且相互独立。
1.2 方差分析的条件
1)可比性:若各组均数本身不具有可比性则不适用方差分析;
2)正态性:偏态分布数据不适用,可使用変量変换方法变为正态或近似正态分布再进行方差分析;
3)方差齐性:若组间方差不齐则不适用方差分析;
2.单因子方差分析及数据准备;
2.1 单因子方差分析
为了考察某个因素A对试验指标(即随机变量X)的影响,在试验时保持其他因素不变,而仅让因素A改变,这种试验称为单因子试验。在方差分析中总假定各组总体独立地服从同方差正态分布,试验的目的就是检验该假设是否成立。如果假设成立则认为因素A对试验指标没有显著影响,试验指标变量的不同是由随机因素引起的,反之,则认为因素A对试验指标有显著性影响。
2.2 统计分析变量
总平均值:
![]()
组平均值:
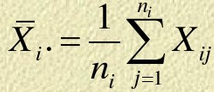
总离差平方和ST、组内离差平方和、组间离差平方和:
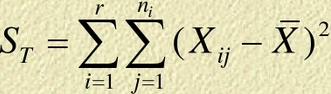
组内离差平方和:
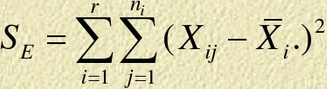
组间离差平方和:
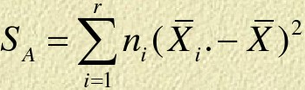
F值

2.3 方差分析表

以上表格可以得出某个因素对某个指标的影响是否显著;
2.4 显著性确定
根据求解的F值,查表获取显著性水平,判断显著性的大小;
附查表链接
3.单因子方差分析法的matlab实现;
clc
clear
close all
%单因子方差分析法:
A = [31.9 27.9 31.8 28.4 35.9;
24.8 25.7 26.8 27.9 26.2;
22.1 23.6 27.3 24.9 25.8;
27.0 30.8 29.0 24.5 28.5 ];
B = A';
p = anova1(B);
[p1, c1, s1] = anova1(B);
cc1 = multcompare(s1);%多重比较检验
%or
C = B(:);
gr = [ones(5,1); ones(5,1)*2; ones(5,1)*3; ones(5,1)*4];
pp = anova1(C, gr);
[p2, c2, s2] = anova1(C, gr);
cc2 = multcompare(s2);%多重比较检验
多个指标的F检验可考虑使用anova等函数;
4.特征的多重比较检验;
F检验的显著性水平满足要求,仅能说明某个因素对试验指标有影响,即总体上该指标在不同的因素水平间有差异性,但不能说明在任意两个因素水平间都存在差异,为了进一步分析指标在不同因素水平间的差异性,采用多重比较检验的方法,对指标进行更详细的差异性检验。

具体可参考MATLAB中的multcompare函数,其中第四列表示均值差的统计观测量,第3/5列表示95%置信区间的左右端点,第六列表示显著性,置信区间包含原点则无显著性差异;
参考
2.方差分析
3.方差分析方法
4.CSDN大牛博客
完