
解法一(面积)
如下图所示,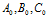 代表三只蜗牛的初始位置。
代表三只蜗牛的初始位置。
图1
经过很短的时间,三只蜗牛分别运动到了 。因为时间很短所以
。因为时间很短所以 在蜗牛
在蜗牛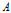 的运动方向上,即
的运动方向上,即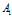 在直线
在直线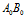 上。同理
上。同理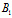 、
、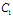 也分别在
也分别在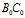 、
、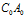 上。三只蜗牛的运动速度相等,所以
上。三只蜗牛的运动速度相等,所以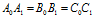 ,这样三角形
,这样三角形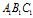 也是一个等边三角形。
也是一个等边三角形。
再经过一个很短的时间,三只蜗牛运动到了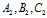
再经过一个很短的时间,三只蜗牛运动到了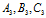
……
也就是说:三只蜗牛在运动过程中,始终保持等边三角形的形状。同时,这个等边三角形一边在旋转一边在缩小,当缩小至一个点(重心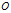 )时三只蜗牛相遇。
)时三只蜗牛相遇。
现在看看三角形边长、旋转角是如何随时间变化的。
考察三角形的面积,可知:
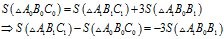
边长为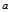 的等边三角形,其面积为
的等边三角形,其面积为

上式两边微分,可得
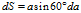
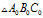 与
与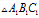 的边长分别为
的边长分别为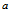 、
、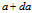 ,所以根据上式可知
,所以根据上式可知
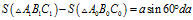
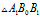 的面积计算公式有两个:
的面积计算公式有两个:
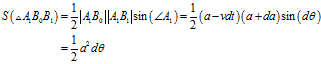
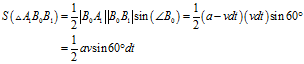
公式代入公式,可得
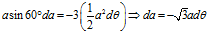
公式代入公式,可得
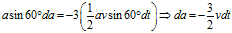
上面两个公式是在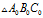 附近推导得出的,但是同样适用于
附近推导得出的,但是同样适用于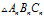 。换句话说就是:在三只蜗牛的运动过程中,上面两个公式是一直都成立的。
。换句话说就是:在三只蜗牛的运动过程中,上面两个公式是一直都成立的。
根据公式可知三角形边长随时间变化的函数为:
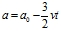
上式中的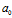 表示等边三角形的初始边长,即
表示等边三角形的初始边长,即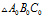 的边长。
的边长。
令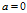 可得
可得
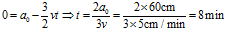
上式表明:运动8分钟后,三角形的边长将变为零,此时三只蜗牛相遇于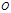 点。三只蜗牛各自爬行的路程为
点。三只蜗牛各自爬行的路程为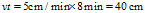 。
。
 中重心
中重心 至各个顶点的距离为
至各个顶点的距离为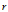 ,则
,则
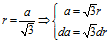
上式代入公式,可得
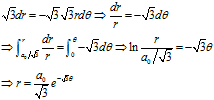
对于蜗牛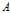 ,以重心
,以重心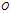 为极点,
为极点,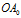 为极轴建立极坐标系。上式就是蜗牛
为极轴建立极坐标系。上式就是蜗牛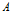 在这个极坐标系下的轨迹方程。可见:蜗牛的运动轨迹是对数螺旋曲线。
在这个极坐标系下的轨迹方程。可见:蜗牛的运动轨迹是对数螺旋曲线。
根据上式可知蜗牛的旋转圈数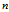 为:
为:
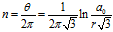
当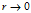 时,
时,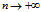 。所以三只蜗牛转了无穷圈。
。所以三只蜗牛转了无穷圈。
解法二(正弦定理)
参考图1,对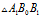 套用正弦定理,有
套用正弦定理,有
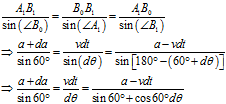
对上式做进一步化简:
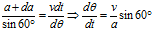
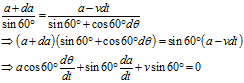
公式代入上式,可得
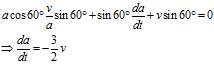
上式除以公式,可得
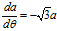
公式分别等价于公式。接下来的解法请参考解法一。
解法三(余弦定理)
参考图1,对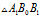 套用余弦定理,有
套用余弦定理,有

上式略去二阶微元,可得
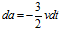
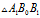 中,
中,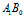 边的高为
边的高为
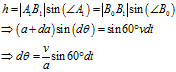
上式的实质其实还是正弦定理。
上面两个公式相除,可得
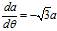
公式分别等价于公式。接下来的解法请参考解法一。
解法四(速度分解)
参考下图,对蜗牛 的速度进行分解:
的速度进行分解:
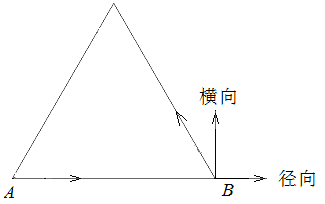
图2
径向速度使两只蜗牛之间的距离增大或减小,其数值为:
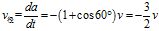
上式中的负号表示两只蜗牛之间的距离随时间的增加而变小。
横向速度使等边三角形旋转,其数值为:
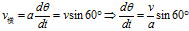
上面两个公式相除,可得:
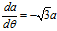
公式分别等价于公式。接下来的解法请参考解法一。
解法五(极坐标)
如下图所示,考察蜗牛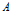 的运动轨迹。以重心
的运动轨迹。以重心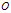 为极点,
为极点,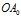 为极轴建立极坐标系。
为极轴建立极坐标系。
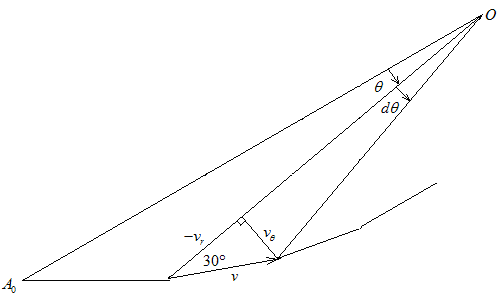
图3
参考图1,这个运动轨迹有一个特点,那就是运动方向与极径的夹角始终为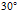 。
。
把运动速度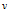 分解为径向速度
分解为径向速度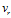 (极径增大为正)与横向速度
(极径增大为正)与横向速度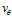 。
。
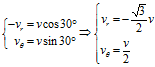
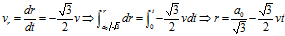
上式中的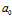 表示等边三角形的初始边长,即
表示等边三角形的初始边长,即 的边长。
的边长。
令上式的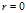 ,可求得
,可求得
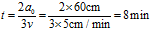
也就是说:三只蜗牛运动8分钟后,将相遇于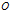 点。三只蜗牛各自爬行的路程为
点。三只蜗牛各自爬行的路程为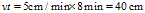 。
。
径向速度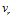 与横向速度
与横向速度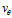 满足下式
满足下式
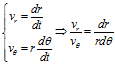
将公式代入上式,可得
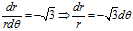
上式两边求定积分,可得
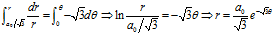
上式表明:蜗牛的运动轨迹是一个对数螺旋曲线。
根据上式可知蜗牛的旋转圈数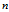 为:
为:
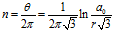
当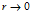 时,
时, 。所以三只蜗牛转了无穷圈。
。所以三只蜗牛转了无穷圈。
解法六(平面直角坐标)
参考图1,以 点为原心,建立
点为原心,建立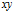 坐标系,如下图所示:
坐标系,如下图所示:
图4
参考等边三角形 。以
。以 为参照物,
为参照物,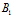 有两个速度,把这两个速度分解为两个:
有两个速度,把这两个速度分解为两个:
一个是平行于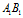 的纵向速度
的纵向速度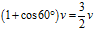 ,这个速度使等边三角形
,这个速度使等边三角形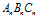 的边长变小。等边三角形
的边长变小。等边三角形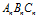 的边长随时间变化的函数为
的边长随时间变化的函数为
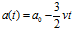
一个是垂直于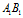 的横向速度
的横向速度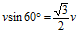 ,这个速度使得运动轨迹的切线方位角
,这个速度使得运动轨迹的切线方位角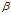 增大,即:
增大,即:
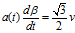
公式代入上式,可得:
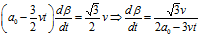
假定经过时间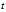 行驶了距离
行驶了距离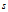 ,则:
,则:
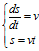
根据公式可得曲率与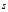 之间的关系:
之间的关系:
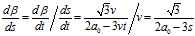
根据上式可知
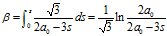
根据上式可知:
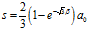
 坐标系内,蜗牛
坐标系内,蜗牛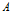 的运动轨迹满足下式
的运动轨迹满足下式
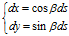
根据公式可知
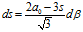
公式代入,再代入公式,可得
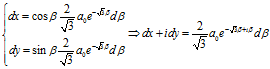
上式两边求定积分,可得
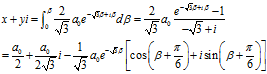
可知:
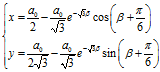
这是一个什么曲线呢?对公式进行变形,可得:
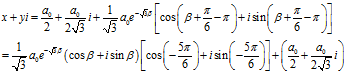
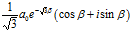 表示以
表示以 坐标系的原点为极点,
坐标系的原点为极点, 轴为极轴,建立极坐标系。极坐标系里有一条曲线,极径
轴为极轴,建立极坐标系。极坐标系里有一条曲线,极径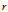 随极角
随极角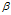 变化的函数为
变化的函数为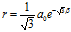 ,这是一条对数螺旋曲线。
,这是一条对数螺旋曲线。
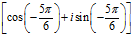 表示旋转曲线。旋转角为
表示旋转曲线。旋转角为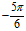 ,即顺时针旋转曲线
,即顺时针旋转曲线 。
。
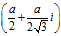 表示旋转后的曲线再平移。其实就是把极点移动至重心
表示旋转后的曲线再平移。其实就是把极点移动至重心 。
。
旋转、平移后的螺旋曲线,极点位于重心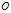 ,极轴与
,极轴与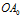 重合。
重合。
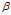 既是切线方位角,又是极坐标系里的极角,其原因在于:极径与切线的夹角始终为一恒定值(
既是切线方位角,又是极坐标系里的极角,其原因在于:极径与切线的夹角始终为一恒定值(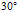 )。另一个解释是:参考图1,
)。另一个解释是:参考图1,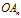 与
与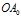 的夹角是极角,
的夹角是极角,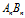 与
与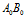 的夹角是切线角,这两个角度均等于三角形
的夹角是切线角,这两个角度均等于三角形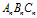 相对于三角形
相对于三角形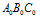 的旋转角。
的旋转角。
结论
1)运动8分钟后,三只蜗牛相遇;
2)三只蜗牛至相遇时,各自爬行了40cm;
3)三只蜗牛的运动轨迹是对数螺旋曲线;
4)三只蜗牛至相遇时,各自转了无穷圈。