先建树
1 typedef struct BiTNode//二叉树的二叉链表存储 2 { 3 int data; 4 struct BiTNode *lchild,*rchild;/* 左右孩子指针 */ 5 }BiTNode,*BiTree; 6 //将BiTree定义为指向二叉链表节点结构的指针类型
递归写法简单又清晰:
先序遍历(DLR)的递归过程为:若二叉树为空,遍历结束。否则:
- 访问根结点
- 先序遍历根结点的左子树
- 先序遍历根结点的右子树
遍历过程如图

1 /* 先序遍历 */ 2 void PreOrder(BiTree bt) 3 { 4 if(bt==NULL) return;/* 递归调用的结束条件 */ 5 Visit(bt->data); /* 访问结点的数据域 */ 6 PreOrder(bt->lchild);/* 先序递归遍历bt的左子树 */ 7 PreOrder(bt->rchild);/* 先序递归遍历bt的右子树 */ 8 }
中序遍历(LDR)的递归过程:
若二叉树非空,则依次执行如下操作:
⑴遍历左子树;
⑵访问根结点;
⑶遍历右子树。
遍历过程如图:
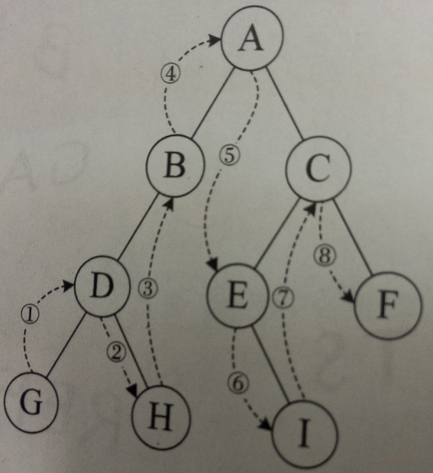
代码如下:
1 /* 中序遍历 */ 2 void InOrder(BiTree bt) 3 { 4 if(bt==NULL) return;/* 递归调用的结束条件 */ 5 InOrder(bt->lchild);;/* 中序递归遍历bt的左子树 */ 6 Visit(bt->data);/* 访问结点的数据域 */ 7 InOrder(bt->rchild);/* 中序递归遍历bt的右子树 */ 8 }
后序遍历(LRD)的递归过程为:
若二叉树为空则结束返回,否则:
(1)后序遍历左子树
(2)后序遍历右子树
(3)访问根结点
遍历过程如图:
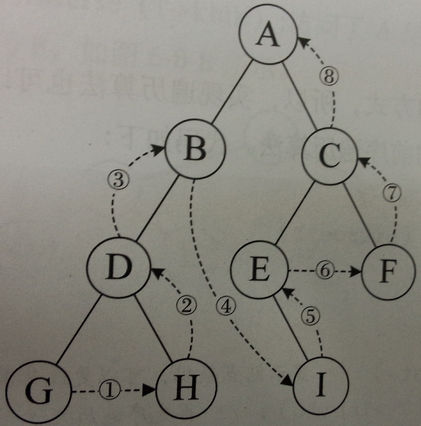
代码如下:
1 /* 后序遍历 */ 2 void PostOrder(BiTree bt) 3 { 4 if(bt==NULL) return;/* 递归调用的结束条件 */ 5 PreOrder(bt->lchild);;/* 后序递归遍历bt的左子树 */ 6 PreOrder(bt->rchild);/* 后序递归遍历bt的右子树 */ 7 Visit(bt->data);/* 访问结点的数据域 */ 8 }
差点忘了放层次遍历(就是忘了
这是我的队列写法(有错的话请一定要指出啊....:
1 /* 层次遍历 */ 2 void LevelOrder(BiTree bt) 3 { 4 queue<BiTree> que; 5 if(bt==NULL) return; 6 que.push(bt);//根结点入队 7 while(!que.empty()) 8 { 9 BiTree front=que.front(); 10 que.pop(); 11 Visit(front->data); 12 if(front->lchild!=NULL)//将队首结点的左孩子结点入队 13 que.push(front->lchild); 14 if(front->rchild!=NULL)//将队首结点的右孩子结点入队 15 que.push(front->rchild); 16 } 17 }
二叉树的元素查找算法:
1 /* 二叉树的元素查找算法 */ 2 BiTree Search(BiTree bt,int x)/* 假装要找的是int */ 3 { 4 BiTree p; 5 p=bt; 6 if(p->data==x) return p; //查找成功返回 7 if(p->lchild!=NULL) return (Search(p->lchild,x));//继续查找 8 if(p->rchild!=NULL) return (Search(p->rchild,x));//继续查找 9 return NULL;//查找失败了::>_<:: 10 }
求二叉树的深度:
1 /* 二叉树的深度运算 */ 2 int treehigh(BiTree bt) 3 { 4 int lh,rh,h; 5 if(bt==NULL) h=0; 6 else 7 { 8 lh=treehigh(bt->lchild); 9 rh=treehigh(bt->rchild); 10 h=(lh>rh?lh:rh)+1; 11 } 12 return h; 13 }