数据结构——树

树的定义以及术语

　　1.树的定义：树（tree）是n（n≥0）个节点的有限集合。当n=0时，称这棵树为空树；当n>0时，该集合满足以下条件:

• (1)有且只有一个特殊的结点称为树的根（root），根结点没有父结点，但有零个或多个直接子节点。（除了根结点之外的所有结点有且只有一个父结点，树的所有结点可以没有子节点也可以有多个子结点）
• (2)除根结点之外的n-1个结点被分为m（m≥0）个互不相交的集合T₁，T₂，……T_m，其中每一个集合Ti（1<=i<=m）本身也是一棵树，被称作原树的子树（subtree）。

　　可以看出，在树的定义中用了递归概念，即用树来定义树。因此，树形结构的算法也常常使用递归方法（比较好写..

　　树也可以这样定义：树是由根结点和若干颗子树构成的。树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的结点，所定义的关系称为父子关系。父子关系在树的结点之间建立了一个层次结构。在这种层次结构中有一个结点具有特殊的地位，这个结点称为该树的根结点，或称为树根。

　　 2.相关术语：

• 节点的度：一个节点含有的子树的个数称为该节点的度；
• 叶节点或终端节点：度为0的节点称为叶节点；
• 非终端节点或分支节点：度不为0的节点；
• 双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
• 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；
• 兄弟节点：具有相同父节点的节点互称为兄弟节点；
• 树的度：一棵树中，最大的节点的度称为树的度；
• 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
• 树的高度或深度：树中节点的最大层次；
• 堂兄弟节点：双亲在同一层的节点互为堂兄弟；
• 节点的祖先：从根到该节点所经分支上的所有节点；
• 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
• 森林：由m（m>=0）棵互不相交的树的集合称为森林；

以图片树3为例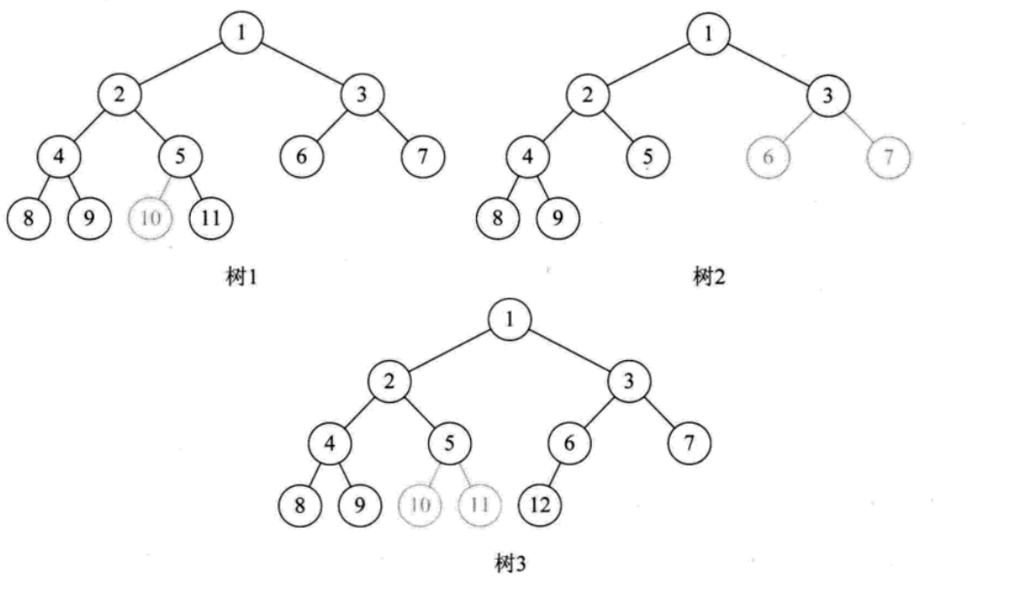

树3的2结点的度为2；8,9,10,11,12为叶子结点（度为0，又称终端结点），除这5个结点之外，树3的其他的结点都是分支结点；对于结点5,结点10,11为它的子结点（在二叉树中，10被称为左孩子结点，11为右孩子结点），结点4是他的兄弟结点（拥有同一个双亲结点2），结点1-2-5-11为结点1到结点5的路径，路径长度为3，则在该路径中，1,2,5都是结点11的祖先，相对而言，11是，1,2,5的子孙，结点11的层数为4，该树深度为4。这三颗树放一起也能叫做森林...（说得略挫

　　3.树的基本操作：

　　（1）Initiate(tree)：初始化一棵空树tree。

　　  (2)  Root(x)：求结点x所在树的根结点。

　　  (3)  Parent(tree,x)：求树tree中结点x的双亲结点。

　　  (4)  Child(tree,x,i)：求树tree中结点x的第i个孩子结点。

　　  (5)  RightSibling(tree,x)：求树tree中结点x右边的第一个兄弟结点（也称右兄弟节点）

　　  (6) Insert(tree,x,i,s)：把以s为根结点的树插入到树tree中座位结点x得第i棵子树

　　  (7) Delete(tree,x,i)：在树tree中删除结点x的第i棵子树。

　　  (8) Traverse(tree)：是树的遍历操作，即按某种方式访问树tree中的每个结点，且使每个结点只被访问一次。遍历操作是非线性结构中非常常用的基本操作，许多对树的操作都是借助该操作实现的。