问题描述
对一个数十进制表示时的每一位数字乘五次方再求和,会得到一个数的五次方数
例如:1024的五次方数为1+0+32+1024=1057
有这样一些神奇的数,它的五次方数就是它自己,而且这样的数竟然只有有限多个
从小到大输出所有这样的数
例如:1024的五次方数为1+0+32+1024=1057
有这样一些神奇的数,它的五次方数就是它自己,而且这样的数竟然只有有限多个
从小到大输出所有这样的数
输出格式
每个数独立一行输出
按照题意,0和1也应该是五次方数。
但是蓝桥杯测评的标准输出是这样

理解为题意没有表达清楚,就按照不考虑0和1的情况来做。
然后暴力遍历一下,这个也是有个细节操作,拆出这个数的每一位,然后直接求这一位的五次方。
1 #include <bits/stdc++.h> 2 using namespace std; 3 int main() { 4 for (int i = 2; i <= 100000000; i++) { 5 int t = i; 6 int sum = 0; 7 while (t != 0) { 8 int a = t % 10; 9 sum += a * a * a * a * a; 10 t /= 10; 11 } 12 if (sum == i) { 13 cout << i << endl; 14 } 15 } 16 return 0; 17 }
输出为
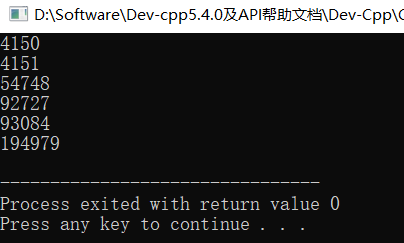
这种题目其实可以先写程序运算好,然后直接输出。
比如改为这样。
1 #include <bits/stdc++.h> 2 using namespace std; 3 int main() { 4 cout << 4150 << endl; 5 cout << 4151 << endl; 6 cout << 54748 << endl; 7 cout << 92727 << endl; 8 cout << 93084 << endl; 9 cout << 194979 << endl; 10 return 0; 11 }
但是还有疑问,写的for循环是2~100000000
有没有可能在上面for循环的范围之外还存在五次方数。
就是怎样证明我们已经找出了所有的五次方数。
证明:
一位数9的五次方数为9^5 = 59049
二位数99的五次方数为9^5 * 2 = 118098
三位数999的五次方数为9^5 * 3 = 177147
为方便叙述,看这个图
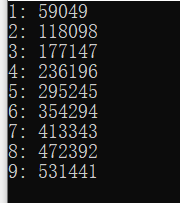
这就发现了,6位数每位全为9的五次方数为6位数,还有可能。
7位数每位全为9的五次方数为6位数。所以绝对不可能存在7位数的五次方数。
就是说位数每加1,最大的五次方数的范围加上9^5,跟不上位数的增长。
所以写个for循环从2~1000000,已经足够找出所有的五次方数了。