【数据结构-图】最短路算法

这篇文章介绍了 2 种图的最短路算法，一种是 Dijkstra 算法，另一种是 Floyd 算法。其中，Dijkstra 算法用来求图中一个节点到其余节点的最短路径（单源最短路径），而 Floyd 算法求的是图中任意两节点间的最短路径（多源最短路径）。

Dijkstra算法

Dijkstra 算法用来求图中一个节点到其余节点的最短路径（单源最短路径）。所以，我们要设置一个起始点 start，我们还需要一个 dist 数组用来存储起始点 start 到其余各点的最短路径，dist[i] 表示起始点 start 到节点 i 的最短路径。我们将已经找到最短路径的节点加入到集合 P，未找到最短路径的节点加入到集合 Q。在代码方面，我们使用 visit 数组来实现，visit[i]=true 表示节点 i 已经找到了 start 到它的最短路径（节点 i 在 P 中），visit[j]=false 表示没有找到 start 到 j 的最短路径（节点 j 在 Q 中）。

首先，我们令 dist[i]=graph[start][i]（这里使用的是邻接矩阵表示的图），有dist[start]=0。我们将 start 加入到集合 P 中，也就是 visit[start]=true。然后，我们在集合 Q 中寻找距离节点 start 路径最短的节点 minNode，此时 start 到 minNode 的最短路径已经确定，就是 graph[start][minNode]，也就是 dist[minNode]，所以我们将 visit[minNode] 设为 true，然后我们使用 minNode 来尝试更新 start 到其他节点的距离，更新方法如下：

• 比较 dist[j]（start 到 j 的距离）、 dist[minNode]（start 到 minNode 之间的距离）加 graph[minNode][j]（minNode 到 j 的距离）的大小；
• 如果 dist[j]>dist[minNode]+graph[minNode][j]，则将 dist[minNode] 更新为 dist[minNode]+graph[minNode][j]；

所以，dijkstra 的算法步骤如下：

• 在集合 Q 中寻找距离起始点 start 最短的节点 minNode;
• 将 minNode 加入到集合 P；
• 尝试使用 minNode 更新 dist 数组；
• 重复上面的过程直到 Q 为空；

代码如下：

/**
* 输入：邻接矩阵表示的图 graph；起始点 start
* 输出：start 到图中其他点的最短距离
*/
vector<int> dijkstra(vector<vector<int>> graph, int start)
{
    int n = graph.size(); // 节点个数
    vector<bool> visit(n, false);   // 标记节点是否已经被加入到已知最短路径的集合P，true表示已加入，false表示未加入
    vector<int> dist(n, INT_MAX);   // 起始点 start 到其余各点的距离
    for(int i=0; i<n; i++)
        dist[i] = graph[start][i];  // dist初始化
    visit[start] = true;

    for(int i=0; i<n-1; i++) // 还有n-1个节点的最短路径没有确定
    {
        int minNode = 0; // 未加入已知最短路径集合中Q到起始点start距离最短的节点编号
        int minDist = INT_MAX;  //
        for(int j=0; j<n; j++)  // 寻找minNode
        {
            if(!visit[j] && dist[j]<minDist)
            {
                minDist = dist[j];
                minNode = j;
            }
        }

        visit[minNode] = true;
        for(int j=0; j<n; j++)  // 根据minNode更新距离
        {
            if(!visit[j] && graph[minNode][j]<INT_MAX)
            {
                if(dist[j]>dist[minNode]+graph[minNode][j])
                    dist[j] = dist[minNode] + graph[minNode][j];
            }
        }
    }
    return dist;
}

注意，上面代码中节点的编号是从 0 开始的，也就是如果有 n 个节点，则节点的编号在 [0, n-1] 之间。

• 时间复杂度：O(n^2)
  n 为节点个数。
• 空间复杂度：O(n)

Floyd算法

Floyd 算法用来求图中任意两节点间的最短路径（多源最短路径）。如果我们想缩短节点 i 和 j 之间的路径 dist[i][j]，我们可以借助第 3 个节点 k，如果 dist[i][j]>dist[i][k]+dist[k][j]，则说明通过 k 来进行中转会使得 i 和 j 之间的路径更短。例如，我们假设 k=1，则：

for(int i=0; i<n; i++)
{
    for(int j=0; j<n; j++)
    {
        if(dist[i][j]<dist[i][1]+dist[1][j])
            dist[i][j]=dist[i][1]+dist[1][j];
    }
}

上面的代码就是通过节点 1 中转来尝试缩小节点 i 到 节点 j 之间的路径。其实，不单单可以通过节点 1 来进行中转，还可以通过其他节点来进行中转，而且，不止可以通过一个节点来进行中转（i->k->j），还可以通过多个节点来进行中转（i->k1->...->kn->j）。为了实现这一思路，我们可以写 3 层循环，其中最外面一层循环代表中转节点的选择：

/**
* 输入：邻接矩阵表示的图 graph
* 输出：图中任意两节点间的最短距离构成的矩阵
*/
vector<vector<int>> floyd(vector<vector<int>> graph)
{
    vector<vector<int>> dist = graph;
    int n = graph.size();
    for(int k=0; k<n; k++)
    {
        for(int i=0; i<n; i++)
        {
            for(int j=0; j<n; j++)
            {
                if(dist[i][j]>dist[i][k]+dist[k][j] && dist[i][k]<INT_MAX && dist[k][j]<INT_MAX)
                    dist[i][j]=dist[i][k]+dist[k][j];
            }
        }
    }
    return dist;
}

• 时间复杂度：O(n^3)
• 空间复杂度：O(1)

完整代码

使用邻接矩阵表示图，如果两个节点之间没有边，则将两节点之间的距离设为 INT_MAX。节点的编号从 0 开始，也就是如果图中有 n 个节点，节点的编号在 [0, n-1] 之间。

#include <iostream>
#include <vector>
using namespace std;

/**
* 输入：邻接矩阵表示的图 graph；起始点 start
* 输出：start 到图中其他点的最短距离
*/
vector<int> dijkstra(vector<vector<int>> graph, int start)
{
    int n = graph.size(); // 节点个数
    vector<bool> visit(n, false);   // 标记节点是否已经被加入到已知最短路径的集合P，true表示已加入，false表示未加入
    vector<int> dist(n, INT_MAX);   // 起始点 start 到其余各点的距离
    for(int i=0; i<n; i++)
        dist[i] = graph[start][i];  // dist初始化
    visit[start] = true;

    for(int i=0; i<n-1; i++) // 还有n-1个节点的最短路径没有确定
    {
        int minNode = 0; // 未加入已知最短路径集合中Q到起始点start距离最短的节点编号
        int minDist = INT_MAX;  //
        for(int j=0; j<n; j++)  // 寻找minNode
        {
            if(!visit[j] && dist[j]<minDist)
            {
                minDist = dist[j];
                minNode = j;
            }
        }

        visit[minNode] = true;
        for(int j=0; j<n; j++)  // 根据minNode更新距离
        {
            if(!visit[j] && graph[minNode][j]<INT_MAX)
            {
                if(dist[j]>dist[minNode]+graph[minNode][j])
                    dist[j] = dist[minNode] + graph[minNode][j];
            }
        }
    }
    return dist;
}

/**
* 输入：邻接矩阵表示的图 graph
* 输出：图中任意两节点间的最短距离构成的矩阵
*/
vector<vector<int>> floyd(vector<vector<int>> graph)
{
    vector<vector<int>> dist = graph;
    int n = graph.size();
    for(int k=0; k<n; k++)
    {
        for(int i=0; i<n; i++)
        {
            for(int j=0; j<n; j++)
            {
                if(dist[i][j]>dist[i][k]+dist[k][j] && dist[i][k]<INT_MAX && dist[k][j]<INT_MAX)
                    dist[i][j]=dist[i][k]+dist[k][j];
            }
        }
    }
    return dist;
}

int main()
{
    int n, m;   // n：节点数，m：边数
    cin>>n>>m;
    vector<vector<int>> graph(n, vector<int>(n, INT_MAX));
    for(int i=0; i<n; i++) graph[i][i]=0;
    for(int i=0; i<m; i++)
    {
        int s, e, val;  // 起始点、终点、边的权重
        cin>>s>>e>>val;
        graph[s][e] = val;
    }
    vector<int> dist = dijkstra(graph, 0);
    cout<<"dijkstra:"<<endl;
    for(auto d:dist) cout<<d<<" ";
    cout<<endl<<endl;

    cout<<"floyd:"<<endl;
    vector<vector<int>> distFloyd = floyd(graph);
    for(int i=0; i<distFloyd.size(); i++)
    {
        for(int j=0; j<distFloyd[i].size(); j++)
        {
            if(distFloyd[i][j]!=INT_MAX && i!=j) cout<<i<<"->"<<j<<"="<<distFloyd[i][j]<<endl;
        }
    }
    return 0;
}

输入：

6 9
0 1 1
0 2 12
1 2 9
1 3 3
2 4 5
3 2 4
3 4 13
3 5 15
4 5 4

输出：

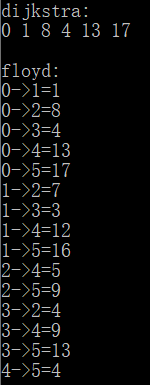
参考

1、https://wiki.jikexueyuan.com/project/easy-learn-algorithm/dijkstra.html
2、https://wiki.jikexueyuan.com/project/easy-learn-algorithm/floyd.html
3、https://www.geeksforgeeks.org/dijkstras-shortest-path-algorithm-greedy-algo-7/
4、https://www.geeksforgeeks.org/dijkstras-shortest-path-algorithm-using-priority_queue-stl/
5、Floyd算法为什么把k放在最外层？