题目描述

输入输出格式
输入格式:
从文件input.txt中读入数据,文件第一行为一个正整数w,其中w < 100,表示有w组数据,即w个账本,需要你判断。每组数据的第一行为两个正整数n和m,其中n < 100,m < 1000,分别表示对应的账本记录了多少个月的收入情况以及偷看了多少次账本。接下来的m行表示刁姹偷看m次账本后记住的m条信息,每条信息占一行,有三个整数s,t和v,表示从第s个月到第t个月(包含第t个月)的总收入为v,这里假设s总是小于等于t。
输出格式:
输出文件output.txt中包含w行,每行是true或false,其中第i行为true当且仅当第i组数据,即第i个账本不是假的;第i行为false当且仅当第i组数据,即第i个账本是假的。
输入输出样例
Solution:
本题是思维比较巧妙的差分约束。。。
思路类似于植树那道题,$u ightarrow v=c$可以理解为$sum[v]-sum[u-1]=c$(前缀和)。
那么对于每个条件我们可以先得出约束条件:$w[u-1,v]=c$表示$sum[v]$比$sum[u-1]$大$c$。
我们直接在这样的图上跑最长路后能求出每个点的$dis$值,但是如何去判断是否合法呢?
先看这张图(手绘勿喷):
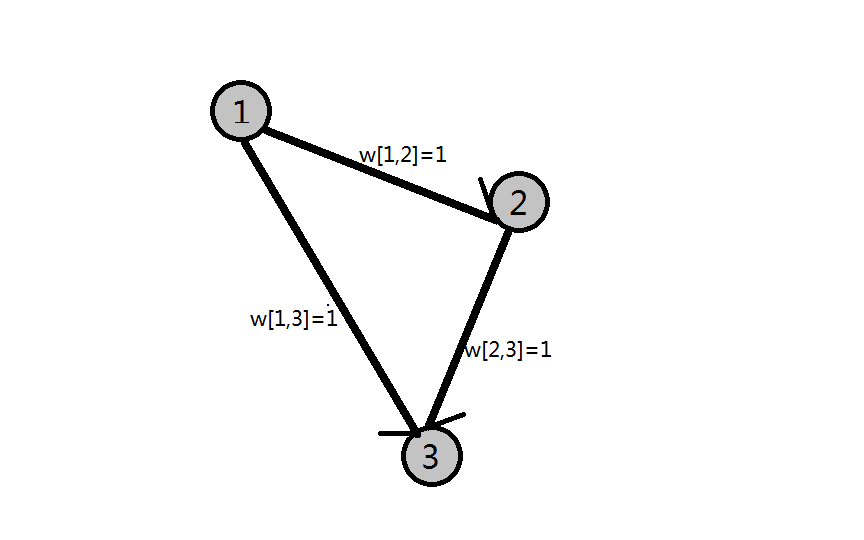
此图表示的是$sum[1,3]=1,;sum[1,2]=1,;sum[2,3]=1$的情况,显然是不合法的情况,但是我们求出最长路后的$dis$值分别为$dis[1]=0,;dis[2]=1;dis[3]=2$,貌似对判断合法没什么用。
不难发现,用少了约束条件,给定的$sum[u
ightarrow v]=c$不仅需要满足$sum[v]-sum[u-1]=c$,还应该满足$sum[u-1]-sum[v]=-c$。
那么我们加入这一约束后,图就变成了这样:
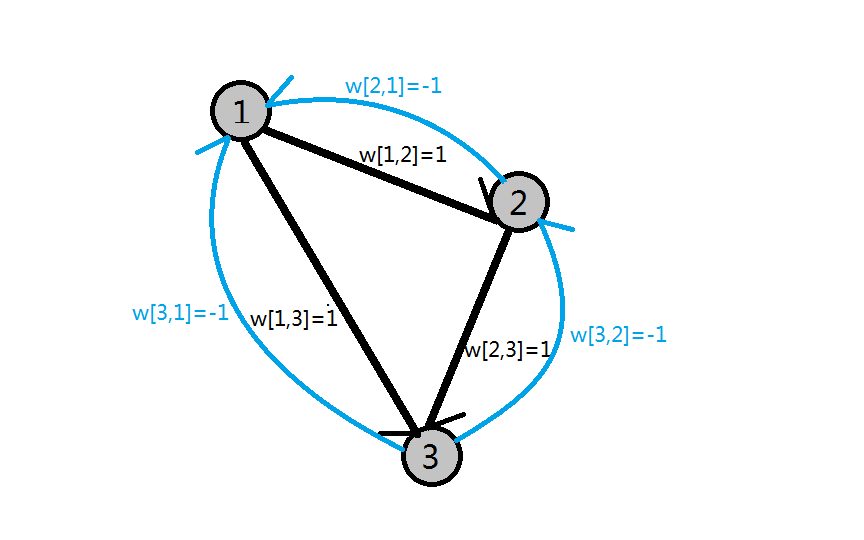
此时,我们由第一张图求得的$dis[1]=0,;dis[2]=1,;dis[3]=2$在此图中还可以继续更新,$dis[1]=0$会由$dis[3]$更新变为$dis[1]=1$,然后引发一系列无限制的更新。究其原因,就是因为不满足$sum[u-1]-sum[v]=-c$这一约束条件。
所以我们将两个约束条件都建成边。
再考虑另一个问题,那就是源点不确定,所以我们每次以没有被遍历过的点为源点跑$spfa$求最长路(即使约束条件中没有出现过该点也对答案无影响,因为根本不会由它进行广搜遍历),那么当某个点被重复遍历超过$n$次,则出现了环,说明不可行,否则就是合法的。(事实证明数据比较水,因为我第一遍没有考虑源点不为$0$的情况,但是却$A$了~~)
代码:
#include<bits/stdc++.h> #define il inline #define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++) using namespace std; const int N=5005,inf=23333333; int T,to[N],tot[N],net[N],h[N],w[N],dis[N],cnt,n,m; bool vis[N]; queue<int>q; il int gi(){ int a=0;char x=getchar();bool f=0; while((x<'0'||x>'9')&&x!='-')x=getchar(); if(x=='-')x=getchar(),f=1; while(x>='0'&&x<='9')a=(a<<3)+(a<<1)+x-48,x=getchar(); return f?-a:a; } il void add(int u,int v,int c){to[++cnt]=v,net[cnt]=h[u],h[u]=cnt,w[cnt]=c;} il bool spfa(int s){ For(i,1,n)dis[i]=-inf; q.push(s);dis[s]=0;vis[s]=1; while(!q.empty()){ int u=q.front();q.pop();vis[u]=0;tot[u]++; if(tot[u]==n)return 0; for(int i=h[u];i;i=net[i]) if(dis[to[i]]<dis[u]+w[i]){ dis[to[i]]=dis[u]+w[i]; if(!vis[to[i]])q.push(to[i]),vis[to[i]]=1; } } return 1; } int main(){ T=gi(); while(T--){ n=gi(),m=gi(); cnt=0; memset(vis,0,sizeof(vis)); memset(h,0,sizeof(h)); memset(tot,0,sizeof(tot)); int u,v,c,f; while(m--){ u=gi(),v=gi(),c=gi(); add(u-1,v,c);add(v,u-1,-c); } f=0; For(i,0,n-1){ if(!tot[i]){ if(!spfa(i)){f=1;break;} } } if(!f)printf("true "); else printf("false "); } return 0; }