数据预处理
先手工生成一些数据,用来说明数据预处理的原理和方法
#导入numpy import numpy as np #导入画图工具 import matplotlib.pyplot as plt #导入数据集生成工具 from sklearn.datasets import make_blobs X,y = make_blobs(n_samples=40,centers=2,random_state=50,cluster_std=2) #用散点图绘制数据点 plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.cool) plt.show()
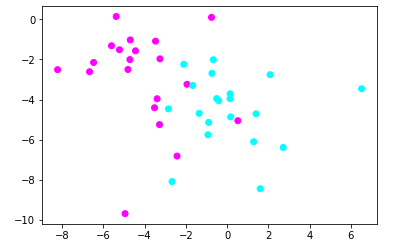
【结果分析】
在使用make_blobs函数时,指定了样本数量n_samples=40,分类centers=2,随机状态random_state=50,标注差cluster_std=2
1.使用StandardScaler预处理数据
原理:
将所有数据的特征值转换为均值为0,方差为1的状态——> 确保数据的“大小”一样,更利于模型的训练
#导入StandardScaler from sklearn.preprocessing import StandardScaler #使用StandardScaler进行数据预处理 X_1 = StandardScaler().fit_transform(X) #用散点图绘制预处理的数据点 plt.scatter(X_1[:,0],X_1[:,1],c=y,cmap=plt.cm.cool) plt.show()

【结果分析】
以上两图,发现数据点的分布情况没有什么不同,但xy轴发生了变化
现在,特征1的数值在-2,3之间
特征2的数值在-3,2之间
2.使用MinMaxScaler数据预处理
#导入MinMaxScaler from sklearn.preprocessing import MinMaxScaler #使用MinMaxScaler进行数据预处理 X_2 = MinMaxScaler().fit_transform(X) #用散点图绘制预处理的数据点 plt.scatter(X_2[:,0],X_2[:,1],c=y,cmap=plt.cm.cool) plt.show()
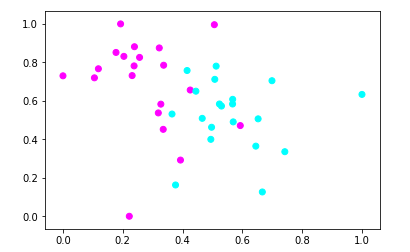
【结果分析】
所有数据的两个特征值都被转换到0-1之间——> 训练速度更快,准确率提高
3.使用RobustScaler数据预处理
和StandardScaler近似
使用中位数和四分位数,直接把一些异常值踢出
#导入RobustScaler from sklearn.preprocessing import RobustScaler #使用RobustScaler进行数据预处理 X_3 = RobustScaler().fit_transform(X) #用散点图绘制预处理的数据点 plt.scatter(X_3[:,0],X_3[:,1],c=y,cmap=plt.cm.cool) plt.show()

【结果分析】
特征1控制在-1.5~2
特征2控制在-2~1.5
4.使用Normalizer数据预处理
将所有样本的特征向量转化为欧几里得距离为1
即,将数据的分布变成一个半径为1的圆(或球)
通常在我们只想保留数据特征向量的方向,而忽略其数值的时候使用
#导入Normalizer from sklearn.preprocessing import Normalizer #使用Normalizer进行数据预处理 X_4 = Normalizer().fit_transform(X) #用散点图绘制预处理的数据点 plt.scatter(X_4[:,0],X_4[:,1],c=y,cmap=plt.cm.cool) plt.show()
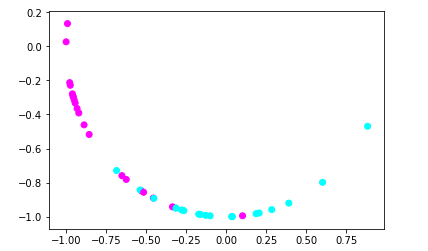
通过数据预处理提高模型的准确率
#导入红酒数据集 from sklearn.datasets import load_wine #导入MLP神经网络 from sklearn.neural_network import MLPClassifier #导入数据集拆分工具 from sklearn.model_selection import train_test_split #建立训练集和测试集 wine = load_wine() X_train,X_test,y_train,y_test = train_test_split(wine.data,wine.target,random_state=62) #打印数据形态 print(X_train.shape,X_test.shape)
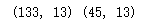
【结果分析】
已成功将数据集拆分为训练集和测试集。训练集样本数量为133个,测试集样本数量为45个
1.用训练集训练一个MLP神经网络,看看在测试集中的得分
#设定MLP神经网络的参数 mlp = MLPClassifier(hidden_layer_sizes=[100,100],max_iter=400,random_state=62) #使用MLP拟合数据 mlp.fit(X_train,y_train) #打印得分 print(mlp.score(X_test,y_test))
0.9333333333333333
2.预处理数据
#使用MinMaxScaler进行数据预处理 scaler = MinMaxScaler() scaler.fit(X_train) X_train_pp = scaler.transform(X_train) X_test_pp = scaler.transform(X_test) #重新训练模型 mlp.fit(X_train_pp,y_train) #得分 print(mlp.score(X_test_pp,y_test))
1.0
【结果分析】
经过数据预处理后,神经网络进行了完美分类
数据降维
数据集中,样本往往有很多特征,这些特征都是同样重要的吗?
是否有一些关键特征对预测的结果起着决定性的作用呢?
1.PCA主成分分析原理
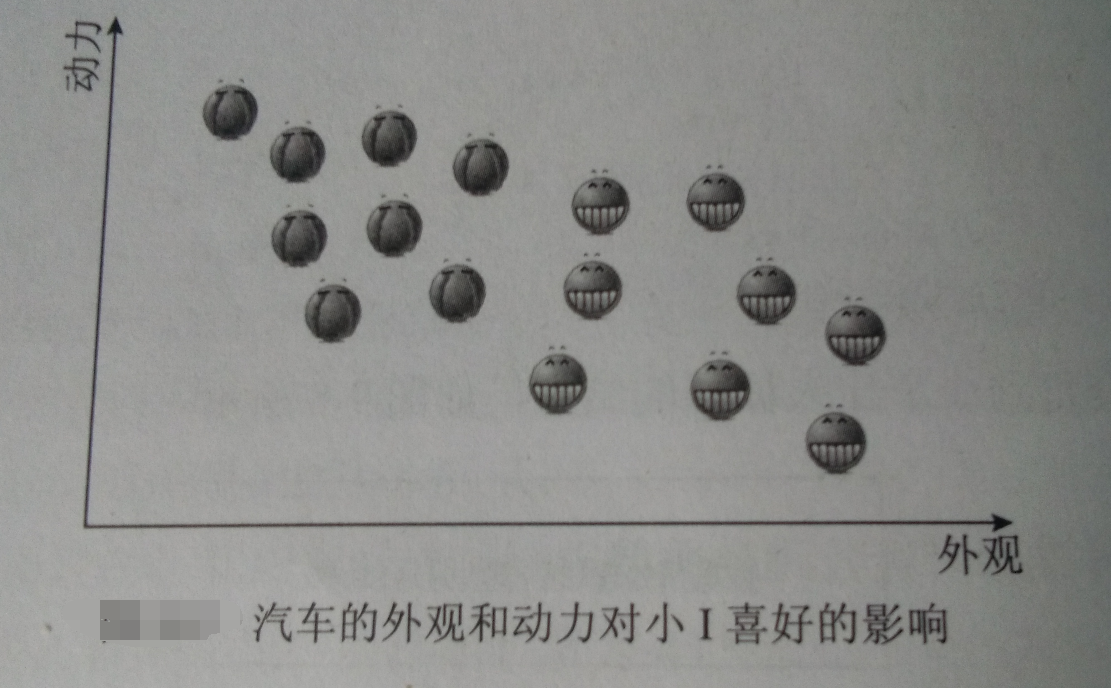
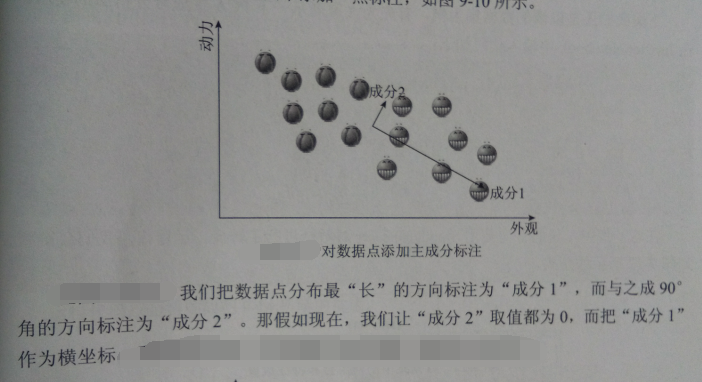

经过这样的处理后,数据集从一个散点组成的面变成了一条直线,即从二维变成了以为,这就是 数据降维
这里用到的方法,即主成分分析法—— PCA
适用数据降维的情况:
- 超高维度数据
- 特征之间有非常强烈的相关性【比如,人口数据中,男性为1,女性为0,去掉其中任何一列,不会丢失任何信息,可以降维,以降低模型的复杂度】
对数据降维以便于进行可视化
#导入数据预处理工具 from sklearn.preprocessing import StandardScaler #对红酒数据集预处理 scaler = StandardScaler() X = wine.data y = wine.target X_scaled = scaler.fit_transform(X) #打印处理后的数据集形态 print(X_scaled.shape)
(178, 13)
接下来导入PCA模块,并对数据进行处理
注意:PCA主成分分析法属于无监督学习算法,所以这里值对X_scaled进行了拟合,而并没有涉及分类标签y
#导入PCA from sklearn.decomposition import PCA #设置生成分数量为2以便可视化 pca = PCA(n_components=2) pca.fit(X_scaled) X_pca = pca.transform(X_scaled) #打印主成分提取后的数据形态 print(X_pca.shape)
(178, 2)
#将三个分类中的主成分提取出来 X0 = X_pca[wine.target==0] X1 = X_pca[wine.target==1] X2 = X_pca[wine.target==2] #绘制散点图 plt.scatter(X0[:,0],X0[:,1],c='b',s=60,edgecolor='k') plt.scatter(X1[:,0],X1[:,1],c='g',s=60,edgecolor='k') plt.scatter(X2[:,0],X2[:,1],c='r',s=60,edgecolor='k') #设置图注 plt.legend(wine.target_names,loc='best') plt.xlabel('component 1') plt.ylabel('component 2') plt.show()
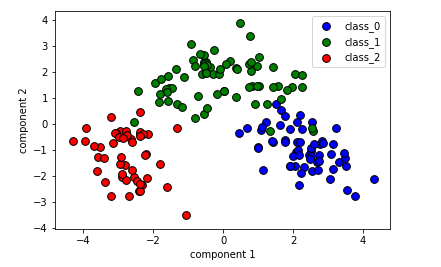
【结果分析】
在之前的章节中,为了进行可视化,只能选取酒数据集的前两个特征,而去掉了其余的11个特征
使用PCA将数据集的特征向量降至二维,从而轻松进行可视化处理,同时不会丢失太多信息
原始特征与PCA主成分之间的关系
酒的数据集中的13个原始特征与经过PCA降维处理后的两个主成分是怎样的关系?
#使用主成分绘制热度图 plt.matshow(pca.components_,cmap='plasma') #纵轴为主成分数 plt.yticks([0,1],['component 1','component 2']) plt.colorbar() #横轴为原始特征数量 plt.xticks(range(len(wine.feature_names)),wine.feature_names,rotation=60,ha='left') plt.show()
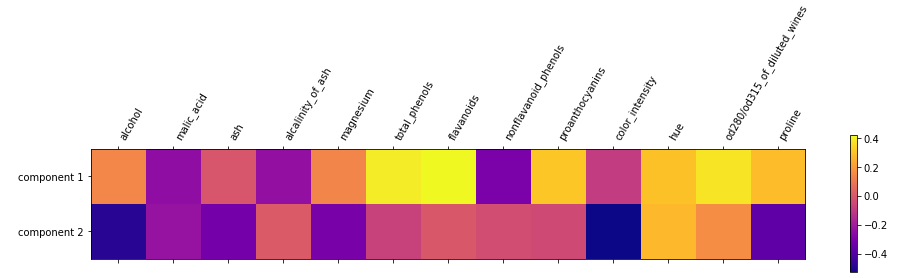
【结果分析】
本图中 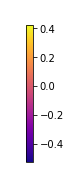 ,不同的颜色表示一个位于-0.5~0.4之间的数值,分别涉及了13个特征
,不同的颜色表示一个位于-0.5~0.4之间的数值,分别涉及了13个特征
如果某个特征对应的数字是正数,则说明它和主成分之间是正相关的关系,如果是负数,则相反

特征提取
由以上,可以得到:
我们通过对数据集原来的特征进行转换,生成新的“特征”或者说“成分”,会比直接使用原始的特征效果更好
1.PCA主成分分析法用于特征提取
这次使用一个复杂一点的数据集——LFW人脸识别数据
#导入数据集获取工具
from sklearn.datasets import fetch_lfw_people
#载入人脸数据集
faces = fetch_lfw_people(min_faces_per_person=20,resize=0.8)
image_shape = faces.images[0].shape
#将照片打印出来
fig,axes = plt.subplots(3,4,figsize=(12,9),subplot_kw={'xticks':(),'yticks':()})
for target,image,ax in zip(faces.target,faces.images,axes.ravel()):
ax.imshow(image,cmap=plt.cm.gray)
ax.set_title(faces.target_names[target])
plt.show()

接下来,再未经处理的情况下,尝试训练一个神经网络:
#导入神经网络 from sklearn.neural_network import MLPClassifier #对数据集拆分 X_train,X_test,y_train,y_test = train_test_split(faces.data/255,faces.target,random_state=62) #训练神经网络 mlp=MLPClassifier(hidden_layer_sizes=[100,100],random_state=62,max_iter=400) mlp.fit(X_train,y_train) print(mlp.score(X_test,y_test))
0.7477064220183486
【结果分析】
在使用2个节点数为100的隐藏层时,神经网络的识别准确率只有0.74
2.使用一些方法来提升模型的表现
A.PCA中的数据白化功能
虽然每个人的面部特征由很大差异,但从像素级别观察图像,差异并不大
且相邻的像素之间有很大的相关性,这样一来,基本特征的输入就是冗余的了,白化的目的就是未了降低冗余性
所以,白化的过程会让样本特征之间的相关度降低,且所有特征具有相同的方差
#使用白化功能处理人脸数据 pca = PCA(whiten=True,n_components=0.9,random_state=62).fit(X_train) X_train_whiten = pca.transform(X_train) X_test_whiten = pca.transform(X_test) #打印白化后数据形态 print(X_train_whiten.shape)
(1306, 99)
【结果分析】
这里我们要求保留原始特征中90%的信息,所以n_components=0.9
可见,经过PCA白化处理后的数据成分为99个,远远小于原始特征数量
#使用白化后的数据训练神经网络 mlp.fit(X_train_whiten,y_train) print(mlp.score(X_test_whiten,y_test))
0.7293577981651376
【结果分析】
书上的得分分别是:神经网络:0.52 PCA 0.57 ——> PCA的数据白化功能对于提高神经网络的准确率是有一定帮助的
B.非负矩阵分解用于特征提取
NMF, 也是一种无监督学习算法
矩阵分解就是一个把矩阵拆解为n个矩阵的乘积
非负矩阵分解,就是原始的矩阵中所有的数值必须大于或等于0,当然分解之后的矩阵中数据也是大于或等于0的

#导入NMF from sklearn.decomposition import NMF nmf = NMF(n_components=105,random_state=62).fit(X_train) X_train_nmf = nmf.transform(X_train) X_test_nmf = nmf.transform(X_test) #打印NMF处理后的数据形态 print(X_train_nmf.shape)
(1306, 105)
【结果分析】
NMF的n_components参数不支持使用浮点数,只能设置为正的整型数
#使用NMF处理后的数据训练神经网络 mlp.fit(X_train_nmf,y_train) print(mlp.score(X_test_nmf,y_test))
0.7591743119266054
聚类算法
有监督学习——主要用于——> 分类和回归
无监督学习——主要用于——> 聚类
分类是算法基于已有标签的数据进行学习并对新数据进行分类
聚类是在完全没有现有标签的情况下,由算法“猜测”哪些数据像是应该“堆”在一起的,并且让算法给不同“堆”里的数据贴上一个数字标签
1.K均值算法

#导入数据集生成工具 from sklearn.datasets import make_blobs #生成分类数为1的数据集 blobs = make_blobs(random_state=1,centers=1) X_blobs = blobs[0] #绘制散点图 plt.scatter(X_blobs[:,0],X_blobs[:,1],c='r',edgecolor='k') plt.show()
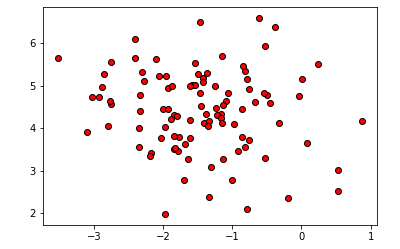
【结果分析】
这段代码,主要是生成一坨没有类别的数据点
make_blobs的centers参数为1,因此这些数据都属于1类
使用K均值帮助这些数据进行聚类:
#导入KMeans工具 from sklearn.cluster import KMeans #要求KMeans将数据聚为3类 kmeans = KMeans(n_clusters=3) #拟合数据 kmeans.fit(X_blobs) #画图 x_min,x_max = X_blobs[:,0].min() -0.5,X_blobs[:,0].max() +0.5 y_min,y_max = X_blobs[:,1].min() -0.5,X_blobs[:,1].max() +0.5 xx,yy = np.meshgrid(np.arange(x_min,x_max,.02),np.arange(y_min,y_max,.02)) Z = kmeans.predict(np.c_[(xx.ravel(),yy.ravel())]) #将每个分类中的样本分配不同的颜色 Z = Z.reshape(xx.shape) plt.figure(1) plt.imshow(Z,interpolation='nearest',extent=(xx.min(),xx.max(),yy.min(),yy.max()),cmap=plt.cm.summer,aspect='auto',origin='lower') plt.plot(X_blobs[:,0],X_blobs[:,1],'r.',markersize=5) #用蓝色叉号表示聚类的中心 centroids = kmeans.cluster_centers_ plt.scatter(centroids[:,0],centroids[:,1],marker='x',s=150,linewidth=3,color='b',zorder=10) plt.xlim(x_min,x_max) plt.ylim(y_min,y_max) plt.xticks(()) plt.yticks(()) plt.show()
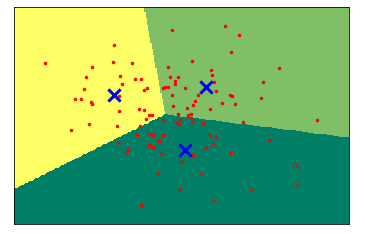
【结果分析】
n_clusters=3,所以K均值将数据点聚为3类
图中的3个蓝色X,代表了K均值对数据进行聚类的3个中心
那么K均值怎样来表示这些聚类?
#打印KMeans进行聚类的标签 print(kmeans.labels_)

【结果分析】
K均值对数据进行的聚类和分类有些类似,是用0、1、2三个数字来代表数据的类,并且存储在 .labels_ 属性中
局限性:
认为每个数据点到聚类中心的方向都是同等重要的——> 对于形状复杂的数据集,K均值算法就不能很好工作
2.凝聚聚类算法

用图像对凝聚算法的工作机制说明:
#导入dendrogram和ward工具 from scipy.cluster.hierarchy import dendrogram,ward #使用连线的方式可视化 linkage = ward(X_blobs) dendrogram(linkage) ax = plt.gca() plt.xlabel("sample index") plt.ylabel("cluster distance") plt.show()
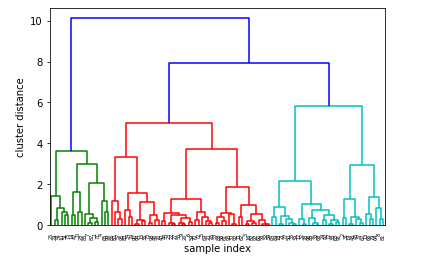
【结果分析】
凝聚聚类算法是自下而上,不断合并相似的聚类中心,以便让类别变少
同时,每个聚类中心的距离也就越来越远
这种逐级生成的聚类方法为:Hierarchy clustering
但,凝聚聚类算法也无法对“形状复杂的数据进行正确的聚类
3.DBSCAN算法
基于密度的有噪声应用空间聚类
通过对特征空间内的密度进行检测,密度大的地方,它会认为是一个类,而密度较小的地方,它会认为是一个分界线
再用之前生成的数据集来展示一下DBSCAN的工作机制:
#导入DBSCAN from sklearn.cluster import DBSCAN db = DBSCAN() #使用DBSCAN拟合数据 clusters = db.fit_predict(X_blobs) #绘制散点图 plt.scatter(X_blobs[:,0],X_blobs[:,1],c=clusters,cmap=plt.cm.cool,s=60,edgecolor='k') plt.xlabel("feature 0") plt.ylabel("feature 1") plt.show()
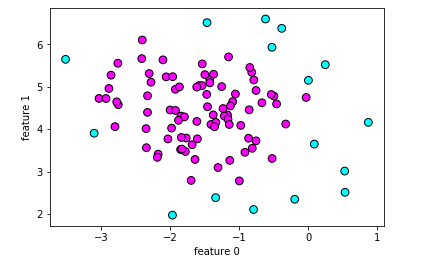
#打印聚类个数 print(clusters)
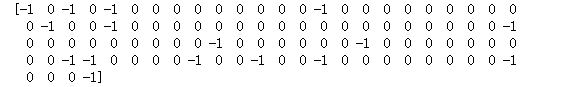
【结果分析】
-1 代表该数据是噪声
中间深色的数据点密度相对较大,所以DBSCAN把它归为一坨
而外围的浅色数据点,DBSCAN认为根本不属于任何一类,所以放在“噪声”一类
eps参数,指考虑化入同一“坨”的样本距离多远
默认0.5
#设置DBSCAN参数eps=2 db_1 = DBSCAN(eps=2) #使用DBSCAN拟合数据 clusters_1 = db_1.fit_predict(X_blobs) #绘制散点图 plt.scatter(X_blobs[:,0],X_blobs[:,1],c=clusters_1,cmap=plt.cm.cool,s=60,edgecolor='k') plt.xlabel("feature 0") plt.ylabel("feature 1") plt.show()
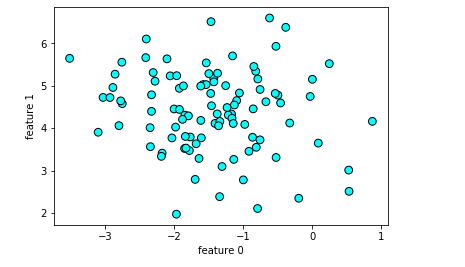
min_samples参数,指定再某个数据点周围,被看成是聚类核心点的个数。越大,则核心数据点越少,噪声就越多
默认是2
#设置DBSCAN的最小样本数为20 db_2 = DBSCAN(min_samples=20) #使用DBSCAN拟合数据 clusters_2 = db_2.fit_predict(X_blobs) #绘制散点图 plt.scatter(X_blobs[:,0],X_blobs[:,1],c=clusters_2,cmap=plt.cm.cool,s=60,edgecolor='k') plt.xlabel("feature 0") plt.ylabel("feature 1") plt.show()
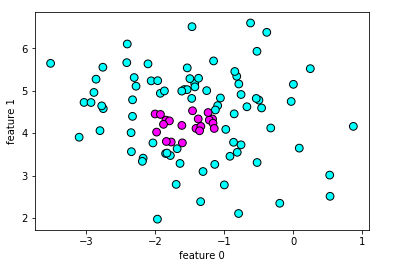
【结果分析】
浅色的数据,也就是噪声变多了
深色的数据,也就是聚类中被划为类别1的数据点少了

对于机器学习来说,合理有效地对数据进行表达是至关重要的
对于没有分类标签的数据来说,无监督学习的聚类算法可以帮助我们更好的理解数据集,并且为进一步训练模型打好基础