源程序:
#include <stdio.h>
#include <stdlib.h>
//#define MAXSIZE 100 /* 存储空间初始分配量 */
const int MAX_INT = 32767;
const int vnum = 20;
typedef struct gp
{
int vexs[vnum]; /* 顶点表 */
int arc[vnum][vnum];/* 邻接矩阵,可看作边表 */
int vexnum, arcnum; /* 图中当前的顶点数和边数 */
}Graph;
struct gpd
{
int adjvex;
int lowcost;
}closedge[vnum];
void CreateGraph(Graph *G)
{
int i, j;
G->arcnum = 6;
G->vexnum = 5;
/* 读入顶点信息,建立顶点表 */
G->vexs[0] = 0;
G->vexs[1] = 1;
G->vexs[2] = 2;
G->vexs[3] = 3;
G->vexs[4] = 4;
//G->vexs[5] = 'F';
//G->vexs[6] = 'G';
//G->vexs[7] = 'H';
//G->vexs[8] = 'I';
for (i = 0; i < G->vexnum; i++)/* 初始化图 */
{
for (j = 0; j < G->vexnum; j++)
{
G->arc[i][j] = MAX_INT;
}
}
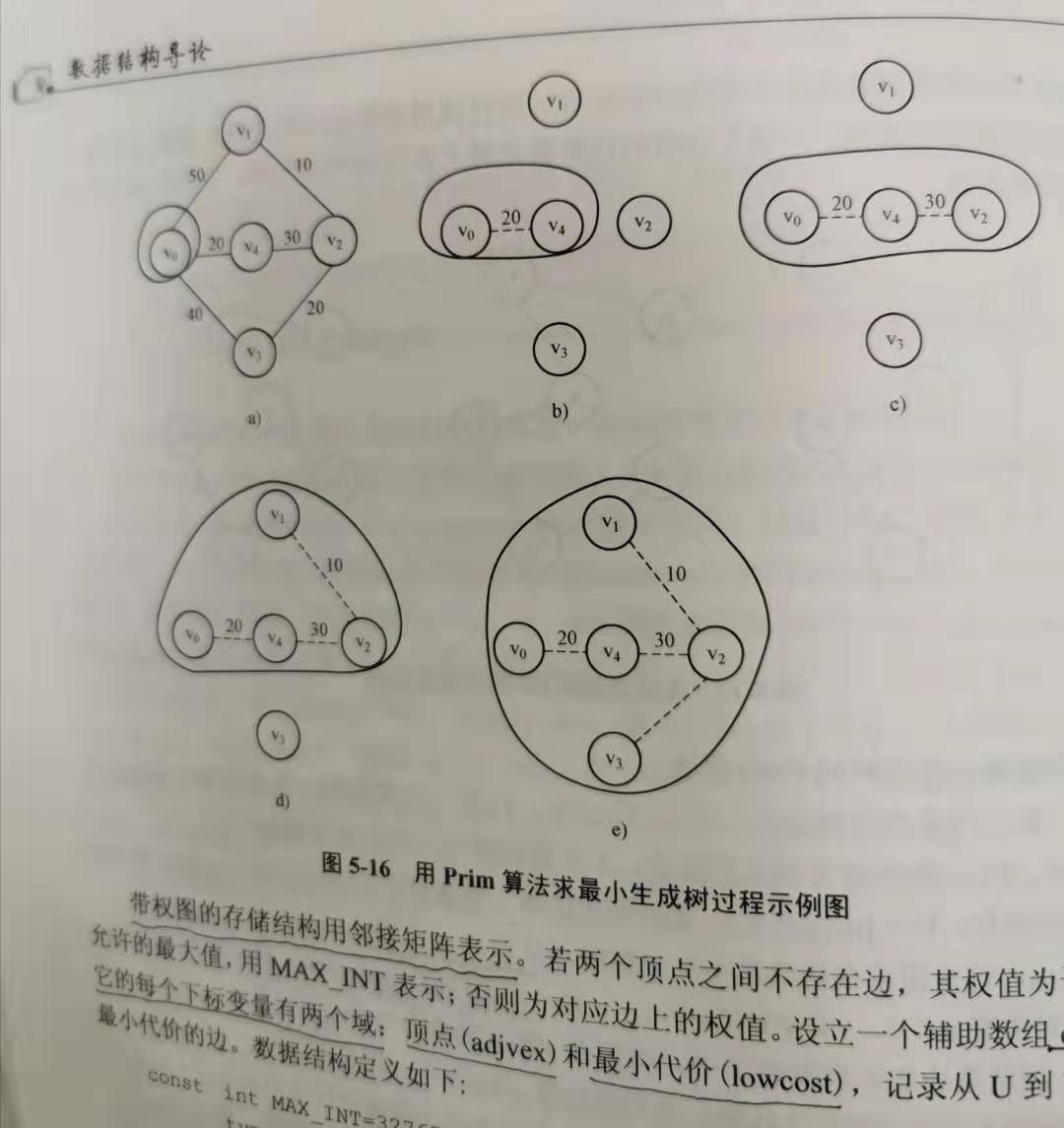
G->arc[0][1] = 50;
G->arc[0][3] = 40;
G->arc[0][4] = 20;
G->arc[1][0] = 50;
G->arc[1][2] = 10;
G->arc[2][1] = 10;
G->arc[2][3] = 20;
G->arc[2][4] = 30;
G->arc[3][0] = 40;
G->arc[3][2] = 20;
G->arc[4][0] = 20;
G->arc[4][2] = 30;
for (i = 0; i < G->vexnum; i++)
{
for (j = i; j < G->vexnum; j++)
{
G->arc[j][i] = G->arc[i][j];
}
}
}
void Printf(Graph *G)
{
printf("顶点数目为: %d ", G->vexnum);
printf("边的数目为: %d ", G->arcnum);
printf("顶点: ");
for (int i = 0; i < G->vexnum; i++)
printf("%d ", G->vexs[i]);
printf(" 邻接矩阵为: ");
for (int i = 0; i < G->vexnum; i++)
{
for (int j = 0; j < G->vexnum; j++) {
if (G->arc[i][j] == MAX_INT)
printf("## ");
else printf("%d ", G->arc[i][j]);
}
printf(" ");
}
}
//PRIM算法
void prim(Graph *g, int u)
{
int v, k, j, min;
//closedge[v].lowcost = 0;
for (v = 0; v < g->vexnum; v++)
if (v != u)
{
closedge[v].adjvex = u;
closedge[v].lowcost = g->arc[u][v];
}
closedge[u].lowcost = MAX_INT;
for (k = 1; k < g->vexnum; k++)
{
min = closedge[k].lowcost; //假设(u,k)具有最小代价
v = k;
for (j = v; j < g->vexnum; j++) //找到真正最小权值的边
if ((closedge[j].lowcost != 0) && (closedge[j].lowcost < min))
{
min = closedge[j].lowcost;
v = j;
}
printf("%d %d ", closedge[v].adjvex, v); //输出生成树的边
closedge[v].lowcost = MAX_INT; //顶点v并入u集
for (j = 0; j < g->vexnum; j++)
if (g->arc[v][j] < closedge[j].lowcost)//如果U与U-V有更小代价的边
{
closedge[j].lowcost = g->arc[v][j];
closedge[j].adjvex = v;
}
}
}
int main()
{
Graph g;
Graph *pg = &g;
CreateGraph(pg);
//printf(" 深度遍历:");
//DFSTraverse(G);
Printf(pg);
printf(" prim最小生成树: ");
prim(pg, 0);
system("pause");
return 0;
}
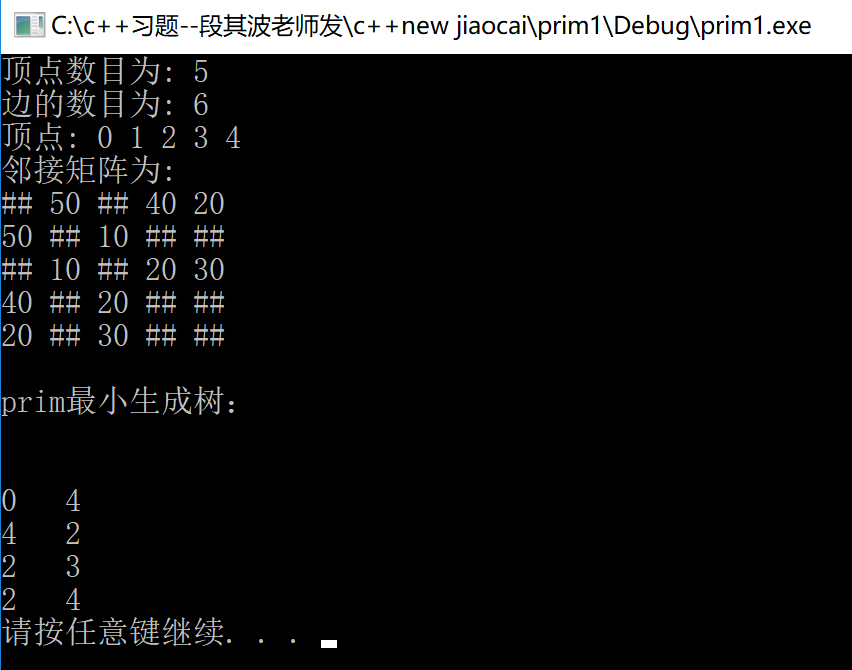
运行结果: