20162322 2017-2018-1 《程序设计与数据结构》第七周学习总结
教材学习内容总结
重要概念、性质的强调
- 度(order):树的度表示树中任意结点的最大子结点数。
- 树的高度(height; 或 深度 , depth):树从根到叶结点的最长路径的长度。
- 满树 与 完全树
- 二叉树的性质
- 性质1:在二叉树的第i层上至多有2i-1个结点(i≥1)。(数学归纳法可证)
- 性质2:深度为k的二叉树最多有2k-1个结点(k≥1)。(由性质1,通过等比数列求和可证)
- 性质3:一棵二叉树的叶子结点数为n0,度为2的结点数为n2,则n0 = n2 + 1。
- 完全二叉树的性质:
- 性质4:具有n个结点的完全二叉树的深度为floor(log2n) + 1 。
- 性质5:如果对一棵有n个结点的完全二叉树(其深度为floor(log2n) + 1 )的结点按层序编号,则对任一结点i(1≤i≤n)有:
- (1) 如果i = 1,则结点i是二叉树的根,无双亲;如果i > 1,则其双亲PARENT(i)是结点 floor((i)/2)。
- (2)如果2i > n,则结点i无左孩子;否则其左孩子LCHILD(i)是结点2i。
- (3)如果2i + 1 > n,则结点i无右孩子;否则其右孩子RCHILD(i)是结点2i + 1。
树的遍历
-
以下所有遍历都是基于先左后右原则
-
所谓的 先序遍历、中序遍历和后序遍历 中的“先”、“中”、“后”指的是结点的相对顺序。
-
已知先序遍历和中序遍历,或后序遍历和中序遍历,可以推出 树 的形状,而已知先序遍历和后序遍历不行。
-
先序遍历
Visit node
Traverse(left-subtree)
Traverse(right-subtree)
- 中序遍历
Traverse(left-subtree)
Visit node
Traverse(right-subtree)
- 后序遍历
Traverse(left-subtree)
Traverse(right-subtree)
Visit node
- 层序遍历
树的根节点入队
当队列不空时
{
结点出队列
Visit node
Traverse(left-subtree)
Traverse(right-subtree)
}
树的实现
教材学习中的问题和解决过程
- 问题1:有关树的遍历,在课上,“已知中,后序构建树”的题难住了我,课下我对这个问题进行了仔细的思考与较深入的研究。
- 问题1解决方案:
- 第一步 弄清了先、中、后序遍历的方式
- 先序:结点,左子树,右子树
- 中序:左子树,结点,右子树
- 后序:左子树,右子树,结点
- 第二步 分别分析先、中、后序遍历的特点
- 1 先序和后序都能在最开始和最后确立整个树的祖先
- 2 根据中序可以分出祖先的左右子树
- 3 迭代以上两步
- 第一步 弄清了先、中、后序遍历的方式
代码调试中的问题和解决过程
- 问题1:书中出现的ArrayIterator并没有找到对应的代码
- 尚未解决
代码托管
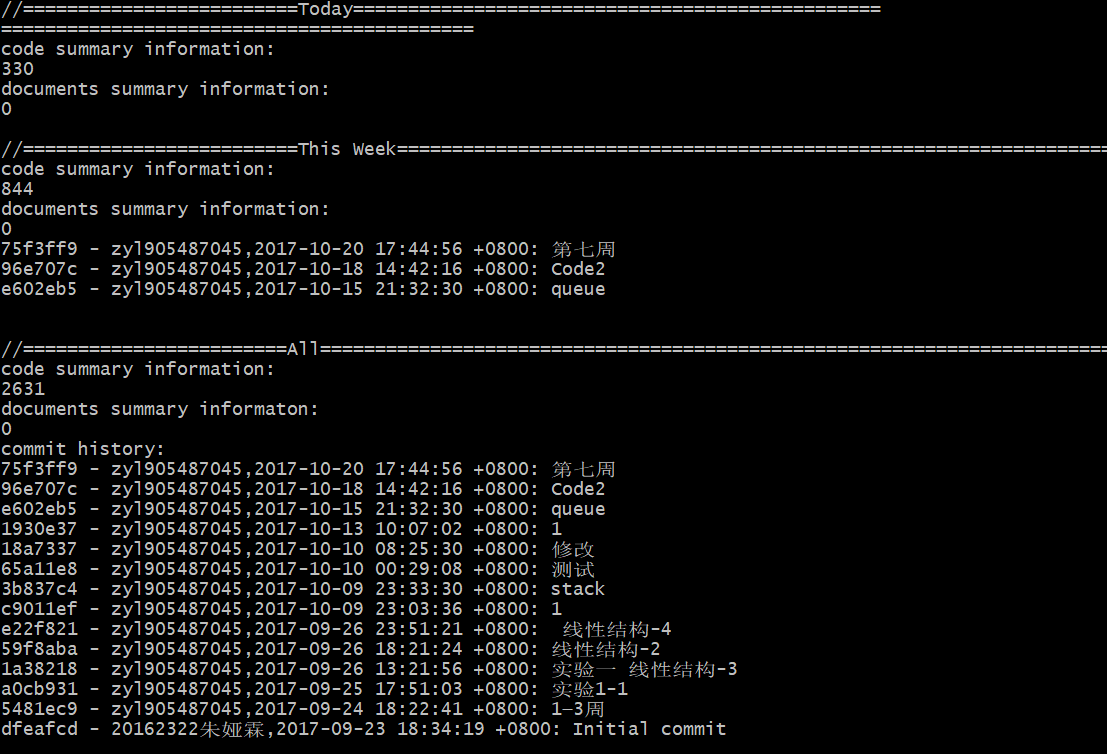
(statistics.sh脚本的运行结果截图)
上周考试错题总结(第四周)
错题1:_________________是一个列表集合,其元素由元素的特征排序。
A. 有序列表 B. 无序列表 C. 索引列表 D. 链表 E. 排列
有序列表具有由元素的固有特征排序的元素。链表或数组可用于实现列表集合。
错题2:添加到扩展ListADT接口的OrderedListADT和UnorderedListADT接口的方法的性质是什么?
A. 它们是将元素添加到列表的方法
B. 它们是从列表中删除元素的方法
C. 它们是删除列表的方法
D. 它们添加一个方法来确定列表中元素的位置
E. 他们添加一个方法来确定列表的大小
添加方法在OrderedListADT接口中定义。AddToFront,addToRear和addAfter方法在UnorderedLIstADT接口中定义。
错题3:Serializable接口允许
A. 从方法中抛出异常。
B. 要读取和写入外部文件的对象。
C. 要添加到列表集合的对象类元素。
D. 编译器警告消息被抑制。
E. 以上都不是
Serializable接口支持从文件写入和读取对象。异常不需要一个接口来抛出。Object类的对象可以使用cast操作符添加到列表集合中。编译器警告消息应该被寻址,而不是被抑制。
错题4:remove操作返回
A. 一个int表示删除后剩余在列表中的元素的数量。
B. 一个布尔值,表示删除是否成功。
C. 被删除的元素
D. 指向列表的指针
E. 删除操作不返回任何这些。
emove操作返回被删除的元素。size方法返回列表中元素数的计数。如果无法找到元素,则remove操作会引发异常。
错题5:将元素添加到有序列表中时,元素按照顺序排列
A. 调用add操作的顺序将它们添加到列表中。
B. 增加存储容量以保持元素
C. 每个元素的关键值
D. 存储器中存储元素的位置的地址。
E. 以上都不能用于确定有序列表中元素的顺序。
有序列表中的每个元素都具有用于确定元素排序的特征。该特性被称为键值。当元素被添加到列表中时,元素的键值将与列表中现有元素的键值进行比较,直到确定元素的正确位置为止。
错题6:链表是在线性列表中组织事物的概念概念
错,链表是一种实现方法,而不是概念概念。列表集合是在线性列表中组织事物的概念概念。
错题7:列表集合的大小是无限制的
对,列表集合可以根据需要增长。
错题8:数组是索引列表的示例
错,虽然数组可能看起来像索引列表的一个例子,但一个重要的区别是数组可能在使用的元素之间有未使用的元素。在具有多个元素的索引列表中,每个元素具有与其相邻的另一个元素。如果从索引列表中删除元素,则元素之间不存在空格。
错题9:用户无法控制无序列表中元素的顺序
错,用户可以将元素添加到无序列表的任一端或将其插入其他元素之间。用户控制列表的顺序。列表无序,因为列表中的元素之间没有固有的关系。
错题10:使用循环数组来进行列表的基于数组的实现将提高从列表中间移除元素的操作的性能
错,从除列表后面的某个地方移除元素需要移动其他元素来缩小间隙。循环数组并不能消除需要移动元素,并且不会对不是循环的数组提供性能改进。
错题11:从列表集合的数组实现中删除元素的操作是O(n)。
对,从n个元素的列表中删除元素将需要总共n个元素的比较和偏移。如果要删除的元素是第一个元素,则需要1次比较和(n-1)个移位。如果要删除的元素是最后一个元素,那么它需要n个比较和没有移位。如果元素位于列表的位置i,那么我有比较和(ni)移位。
错题12:remove操作返回一个布尔值,指示是否在列表中找到要删除的元素。
错,remove操作返回要删除的元素。如果未找到该元素,则会抛出异常。用户程序可以检测异常并进行处理。
结对及互评
点评:
- 博客中值得学习的或问题:
- 最近周楠学习特别认真,特别努力,要一起加油哟~
本周结对学习情况
- 20162323
- 结对照片
- 结对学习内容
- 一起做实验
其他(感悟、思考等,可选)
要不怕困难,才能战胜困难;要积极思考,才能真正提高。
加油加油!

学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 20/20 | 绪论 |
| 第二周 | 386/386 | 0/1 | 20/40 | |
| 第三周 | 500/886 | 2/3 | 20/60 | 选择与排序 |
| 第四周 | 300/1186 | 2/4 | 20/80 | 线性表 |
| 第五周 | 300/1486 | 1/5 | 20/100 | 栈 |
| 第六周 | 300/1786 | 2/7 | 20/120 | 队列 |
| 第七周 | 844/2630 | 3/10 | 20/140 | 树 |
-
计划学习时间:20小时
-
实际学习时间:20小时
-
改进情况:多思考!多思考!