我们先看一下题目：
（有没有和我一样的朋友看到这道题以为是几何不可做题
这个题目真的很难理解，并且样例也给得太水了吧！
理解题目是必不可少的（这并不是你看了半小时题目的理由）——首先我们先简化题目
1：有n个连续函数fi(x)这句话放在平面直角坐标系内就是有n条直线（应该挺好理解的这句话）
2：对于任意fi(x)和fj(x)，都有一个值x使两个相等等同与任意两条直线交于一点
3：不存在fi(x)=fj(x)=fk(x)就是不会有三条及以上的直线交于同一点
我们在这里便做一个总结：
题目给我们的意思是——在一个平面直角坐标系内有n条直线，两两相交于一点，不存在三条及以上的直线交于同一点；
接下来我们再解释第几层——
我们便以样例的图来说明：
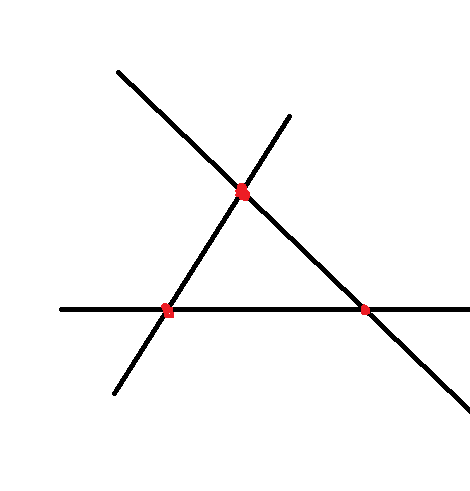
我们先将这三条线段画出来，将他们的交点来聚焦，再将三条线段染上颜色，层数怎么划分应该很明显了吧（着实不是很好理解，可以自己多手画几幅图）
我们看重点，也就是题目所求我们应该怎么办——
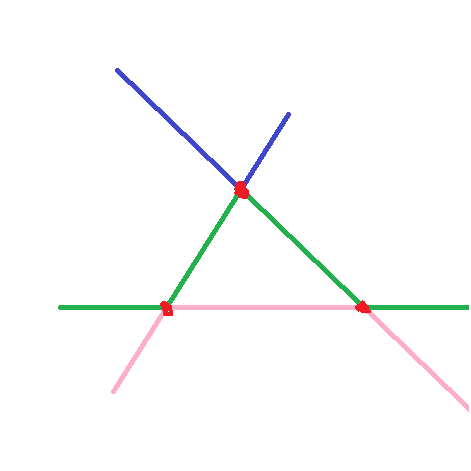依旧是上面那副图，首先我们看第一层（蓝色），不用想，这一层的最小值是2，同理第二层（绿色）的最小值是4。
然后我们看第三层（你是不是以为我又要同理说是3了），这道题最神奇的地方就在这。
我们完全可以将这幅图旋转一下，这时第三层就变成了原先的第一层，最小值也就是2了。看到这里，我们便发现了一个重要性质：答案具有对称性！具体来说是k(k<n/2)与n-k+1的答案一样！
所以我们只需要思考前n/2的答案就可以。
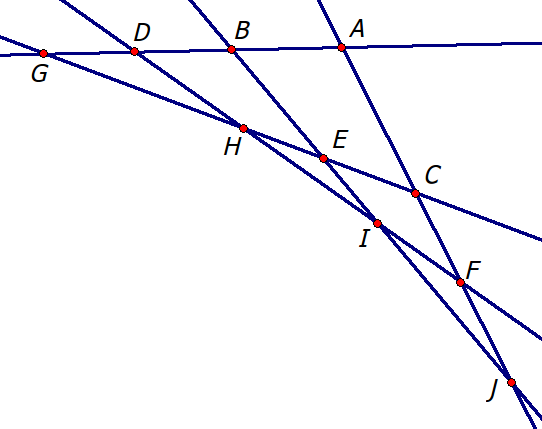我们看到这张图 我们可以发现第一层1个点，第二层2个点，第三层3个点.......我们可以证明这样一定是最优的，首先两点必定交于一点，那么第一层便只有一个点，在第二层假如最小不为2，那就是1~2-1中的一个（在第二层看来其实就是1啦）但是第二层需要第三条线，如果不为2那么第三条线与第一，第二条线的交点就为1，那么就与题目中的不存在fi(x)=fj(x)=fk(x)相矛盾，同样的我们可以这样一直扩展，可以得知假如第k（k<n/2）层的交点数比k小，那么必有三线或三线以上交于同一点，与题目矛盾，所以第k(k<n/2)层最小为k点。
看图得知：为这一层的线段有关的点不仅包括本层还与上一层有关。
所以可知：第一层：1
第二层：1+2
第三层：2+3
。。。。。。
又因为线段数为点数加1，我们便得到了最终答案：2，4，6，8.......。
所以我们可以归纳一下：n==1时 答案=1；
n!=1&&k<=n/2时，答案=2*k;
n!=1&&k>n/2时，答案=2*（n-k+1）;
所以就可以愉快的贴代码啦
#include<iostream> #include<cstdio> using namespace std; long long n,k,ans; int main() { scanf("%lld%lld",&n,&k); if(n==1) printf("1"); else if(k<=n/2) printf("%lld",2*k); else printf("%lld",2*(n-k+1)); return 0; }
(果然结论题代码都很短啊)
（那么慢走）
（不懂可以加qq2733524923我们一起探讨）