前言:这个.....难度有点超a....
T1:嘤
首先要观察出结论,2*2的小矩阵满足记为1,不满足记为0,那么求最大的1矩阵,还是很好证明的,推一下.....主要是这个找最大1矩阵得优化为O(n*m)的
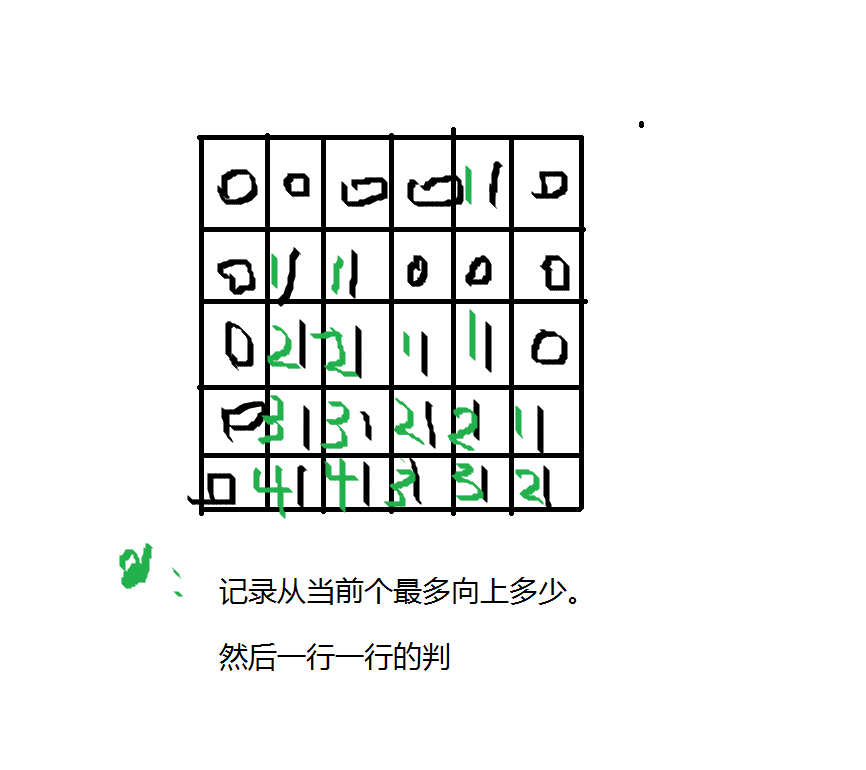
主要是加个单调栈维护....
上代码:
1 #include<bits/stdc++.h> 2 #define maxn 1005 3 using namespace std; 4 int n,m,a[maxn][maxn]; 5 int vis[maxn][maxn]; 6 int st[maxn],top=0; 7 void init(){ 8 scanf("%d%d",&n,&m); 9 for(int i=1;i<=n;i++) 10 for(int j=1;j<=m;j++) scanf("%d",&a[i][j]); 11 12 for(int i=1;i<=n;i++) 13 for(int j=1;j<=m;j++) vis[i][j]=1; 14 15 for(int i=2;i<=n;i++) 16 for(int j=2;j<=m;j++){ 17 if(a[i-1][j-1]+a[i][j]<=a[i][j-1]+a[i-1][j]) vis[i][j]=vis[i][j-1]+1; 18 } 19 for(int i=1;i<=n;i++){ 20 for(int j=1;j<=m;j++){ 21 if(vis[i][j]==1) vis[i][j]=0;//大格格到小格格 22 } 23 } 24 25 st[0]=1; 26 int maxx=0; 27 for(int j=2;j<=m;j++){//要加个单调栈优化 28 top=0; 29 for(int i=2;i<=n;i++){ 30 while(top&&vis[i][j]<=vis[st[top]][j]){//小于等于保证是0就续接 31 maxx=max(maxx,vis[st[top]][j]*(i-st[top-1]));//让前一个被计算完 32 top--; 33 } 34 st[++top]=i;//加进去重新开始记 35 } 36 while(top){//将前面的小的计算完,可以贯穿全部的23333 37 maxx=max(maxx,vis[st[top]][j]*(n+1-st[top-1]));//贯穿全部,细节!!! 38 top--; 39 } 40 } 41 42 printf("%d",maxx); 43 } 44 int main(){ 45 init(); 46 47 return 0; 48 }
T2:
考基本算法的一个,首先要跑出最短路图,方法:
正反跑一遍最短路,然后对于每条边,设其两节点为u,v,若dist1[u]+distn[v]+这条边边权==dist1[n],则将这条边加入到最短路图中。
然后对于最短路图求出桥边,即可。这样删去桥边最短路就只有增大。
上代码:
1 #include<bits/stdc++.h> 2 #define maxn 100005 3 using namespace std; 4 int n,m,x,y,z; 5 struct eage{ 6 int from,to,next,len; 7 }e[maxn<<1]; 8 int np=0,first[maxn]; 9 int dist1[maxn],distn[maxn]; 10 bool vis[maxn]; 11 struct node{ 12 int v,id; 13 friend bool operator <(node a,node b){ 14 return a.v>b.v; 15 } 16 }; 17 struct eagee{ 18 int to,next,id; 19 }ee[maxn<<1]; 20 int npp=0,fir[maxn]; 21 void add1(int u,int v,int id){ 22 ee[++npp]=(eagee){v,fir[u],id}; 23 fir[u]=npp; 24 } 25 void bfs(int s,int *dist){ 26 priority_queue<node>q; 27 for(int i=1;i<=n;i++) dist[i]=0x3f3f3f3f; 28 memset(vis,0,sizeof(vis)); 29 dist[s]=0; 30 q.push((node){dist[s],s}); 31 while(!q.empty()){ 32 node t=q.top();q.pop(); 33 int i=t.id; 34 if(vis[i]) continue; 35 vis[i]=1; 36 for(int p=first[i];p;p=e[p].next){ 37 int j=e[p].to,c=e[p].len; 38 if(dist[j]>dist[i]+c){ 39 dist[j]=dist[i]+c; 40 q.push((node){dist[j],j}); 41 } 42 } 43 } 44 } 45 void add(int from,int u,int v,int len){ 46 e[++np]=(eage){from,v,first[u],len}; 47 first[u]=np; 48 } 49 int st[maxn],top=0; 50 int dfn[maxn],clock_=0,low[maxn]; 51 bool viss[maxn]; 52 void tarjan(int i,int fb){ 53 viss[i]=1; 54 dfn[i]=low[i]=++clock_; 55 for(int p=fir[i];p;p=ee[p].next){ 56 int j=ee[p].to,id=ee[p].id; 57 if(id==fb) continue; 58 if(viss[j]){ 59 if(dfn[j]<dfn[i]) low[i]=min(low[i],dfn[j]); 60 continue; 61 } 62 tarjan(j,id); 63 low[i]=min(low[i],low[j]); 64 } 65 if(low[i]==dfn[i]&&fb!=0){ 66 st[++top]=fb; 67 } 68 } 69 void init(){ 70 scanf("%d%d",&n,&m); 71 for(int i=1;i<=m;i++){ 72 scanf("%d%d%d",&x,&y,&z); 73 add(x,x,y,z); 74 add(y,y,x,z); 75 } 76 bfs(1,dist1); 77 bfs(n,distn); 78 79 for(int i=1;i<=np;i++){ 80 int u=e[i].from,v=e[i].to,len=e[i].len; 81 int id=((i&1)?i/2+1:i/2); 82 if(dist1[u]+len+distn[v]==dist1[n]) 83 add1(u,v,id),add1(v,u,id); 84 } 85 86 tarjan(1,0); 87 sort(st+1,st+top+1); 88 printf("%d ",top); 89 for(int i=1;i<=top;i++){ 90 printf("%d ",st[i]); 91 } 92 } 93 int main(){ 94 init(); 95 96 return 0; 97 }