主要思想:
- 计算思维:模拟比赛过程,自动化执行N场比赛(当N越大时,比赛结果的分析就越科学)
- 自顶向上:分而治之,大问题转化为各个小问题
- 自顶向下:模块化,可小模块测试后组装,是自顶向上的反过程
实例:

自顶向下流程图

代码
from random import random
def printIntro():#输入提示语句
print("这个程序模拟两个选手A和B的某种竞技比赛")
print("程序运行需要A和B的能力值(以0到1之间的小数表示)")
def getInputs():#获得能力值和比赛场数
a = eval(input("请输入选手A的能力值(0-1): "))
b = eval(input("请输入选手B的能力值(0-1): "))
n = eval(input("模拟比赛的场次: "))
return a, b, n
def gameOver(a,b):#游戏结束条件
return a==15 or b==15#a或b分数达到15分
def simOneGame(probA, probB):#模拟一场比赛
scoreA, scoreB = 0, 0
serving = "A"#serving表示发球方
while not gameOver(scoreA, scoreB):#当比赛不结束时
if serving == "A":
if random() < probA:#调用random获得一个随机变量,如果小于A,(在A的能力范围内),
scoreA += 1#A得一分
else:
serving="B"#反之,B得一分
else:#当发球方交换时(B)
if random() < probB:#同上
scoreB += 1
else:
serving="A"
return scoreA, scoreB#返回A,B最后的分数
def simNGames(n, probA, probB): # 基于模拟一场比赛模拟N场比赛
winsA, winsB = 0, 0
for i in range(n): # 循环N次
scoreA, scoreB = simOneGame(probA, probB) # 调用模拟一场比赛
if scoreA > scoreB:
winsA += 1 # 如果A的分数>B,A的获胜次数加一
else:
winsB += 1 # 如果A的分数<B,B的获胜次数加一
return winsA, winsB # 返回获胜次数
def printSummary(winsA, winsB):#打印出比赛结果
n = winsA + winsB
print("竞技分析开始,共模拟{}场比赛".format(n))
print("选手A获胜{}场比赛,占比{:0.1%}".format(winsA, winsA / n))
print("选手B获胜{}场比赛,占比{:0.1%}".format(winsB, winsB / n))
def main():
printIntro()
probA, probB, n = getInputs()
winsA, winsB = simNGames(n, probA, probB)
printSummary(winsA, winsB)
main()
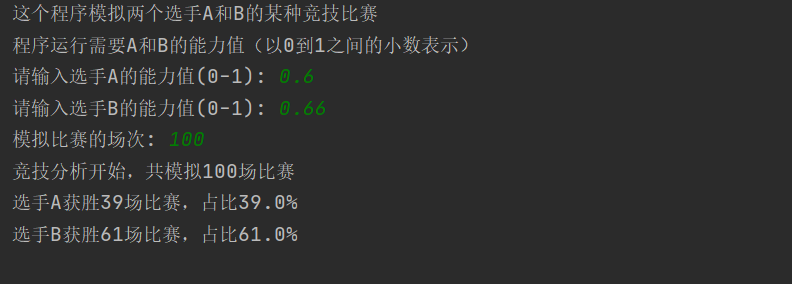
结果