cqyz oj | 约数和加强版 | 乘法逆元 | 唯一分解定理

------------恢复内容开始------------

Description

求 A^X 所有约数和，结果 mod B（其中B是一个质数）。

Input

第一行为整数T和A。接下来的T行，每行包含两个整数：X B，其中B是一个质数。

Output

输出T行，对于每个输入的X和B，输出A^x的约数和mod B的结果。

Sample Input 1 

2 2004
1 29
10000 29

Sample Output 1

6
10

Hint

0<A,B,X<=10^9，最多100000组数据

---

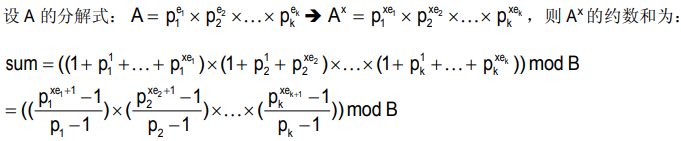
 因为B是质数，式中除法可用乘法逆元计算。

#include<bits/stdc++.h>
#define mst(a, b) memset(a, b, sizeof(a))
using namespace std;
const int maxn = 5005;
typedef long long LL;

LL read() {
    LL o=0, f=1;
    char ch;
    while(!isdigit(ch=getchar())) if(ch == '-') f=-1;
    while(isdigit(ch)) o=o*10+ch-'0', ch = getchar();
    return o*f;
}

LL Exgcd(LL a, LL b, LL &x, LL &y) {
    if(!b) { x=1, y=0; return a; }
    LL g = Exgcd(b, a%b, y, x);
    y = y - a / b * x;
    return g;
}

LL inverse(LL a, LL n) {
    LL x, y, g = Exgcd(a, n, x, y);
    return g == 1 ? (x%n+n)%n : -1;
}

vector<int> p, e;
int fj(int x) {
    p.clear(), e.clear();
    for(int i=2, t, x0=x; i*i<=x0; i++) {
        if(x%i == 0) {
            t=0;
            while(x%i == 0) x/=i, t++;
            p.push_back(i);
            e.push_back(t);
        }
    }
    if(x>1) p.push_back(x), e.push_back(1);
    return p.size();
}

LL qkm(LL a, LL b, LL mo) {
    LL r=1;
    while(b) {
        if(b&1) r = r * a % mo;
        a = a * a % mo;
        b >>= 1;
    }
    return r;
}

int main() {
    LL t = read(), A=read(), B, X;
    int n = fj(A);
    while(t--) {
        X=read(), B=read();
        LL ans = 1;
        for(int i=0; i<n; i++) {
            LL t = qkm(p[i], e[i]*X+1, B);
            t = ((t-1)%B+B)%B;
            t = t * inverse(p[i]-1, B) % B;
            ans = ans * t % B;
        }
        printf("%lld
", ans);
    }
    return 0;
}

------------恢复内容结束------------

Description

求 A^X 所有约数和，结果 mod B（其中B是一个质数）。

Input

第一行为整数T和A。接下来的T行，每行包含两个整数：X B，其中B是一个质数。

Output

输出T行，对于每个输入的X和B，输出A^x的约数和mod B的结果。

Sample Input 1 

2 2004
1 29
10000 29

Sample Output 1

6
10

Hint

0<A,B,X<=10^9，最多100000组数据

---

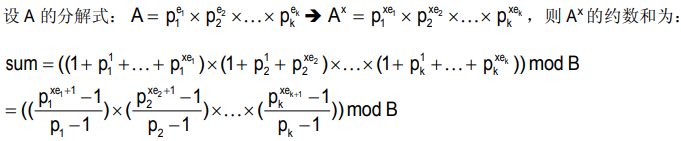
 因为B是质数，式中除法可用乘法逆元计算。

#include<bits/stdc++.h>
#define mst(a, b) memset(a, b, sizeof(a))
using namespace std;
const int maxn = 5005;
typedef long long LL;

LL read() {
    LL o=0, f=1;
    char ch;
    while(!isdigit(ch=getchar())) if(ch == '-') f=-1;
    while(isdigit(ch)) o=o*10+ch-'0', ch = getchar();
    return o*f;
}

LL Exgcd(LL a, LL b, LL &x, LL &y) {
    if(!b) { x=1, y=0; return a; }
    LL g = Exgcd(b, a%b, y, x);
    y = y - a / b * x;
    return g;
}

LL inverse(LL a, LL n) {
    LL x, y, g = Exgcd(a, n, x, y);
    return g == 1 ? (x%n+n)%n : -1;
}

vector<int> p, e;
int fj(int x) {
    p.clear(), e.clear();
    for(int i=2, t, x0=x; i*i<=x0; i++) {
        if(x%i == 0) {
            t=0;
            while(x%i == 0) x/=i, t++;
            p.push_back(i);
            e.push_back(t);
        }
    }
    if(x>1) p.push_back(x), e.push_back(1);
    return p.size();
}

LL qkm(LL a, LL b, LL mo) {
    LL r=1;
    while(b) {
        if(b&1) r = r * a % mo;
        a = a * a % mo;
        b >>= 1;
    }
    return r;
}

int main() {
    LL t = read(), A=read(), B, X;
    int n = fj(A);
    while(t--) {
        X=read(), B=read();
        LL ans = 1;
        for(int i=0; i<n; i++) {
            LL t = qkm(p[i], e[i]*X+1, B);
            t = ((t-1)%B+B)%B;
            t = t * inverse(p[i]-1, B) % B;
            ans = ans * t % B;
        }
        printf("%lld
", ans);
    }
    return 0;
}