在互金公司等各种贷款业务机构中,普遍使用信用评分,对客户实行打分制,以期对客户有一个优质与否的评判。主要有反欺诈评分模型和信用评分卡模型(千元左右的小额短期贷款风控业务的重点工作是信用评分方面),针对已知用户的每个特征进行打分,最后求和与阈值分数对比,以此做出判断,生成的不同变量的不同特征的分数体系即打分卡模型。
信用评分卡:
A卡,Application scorecard。即申请评分卡,用于贷前审批阶段对借款申请人的量化评估;
B卡,Behavior scorecard。即行为评分卡,用于贷后管理,通过借款人的还款及交易行为,结合其他维度的数据预测借款人未来的还款能力和意愿,推测用户是否会逾期;例如用户在某银行贷款后,又去其他多家银行申请了贷款,那可以认为此人资金短缺,可能还不上钱,如果再申请银行贷款,就要慎重放款。
C卡,Collection scorecard。催收评分卡,用于催收管理,在借款人当前还款状态为逾期的情况下,预测未来该笔贷款变为坏账的概率。
三种评分卡使用的时间不同,分别侧重贷前、贷中、贷后(已经逾期之后);另外数据要求不同,A卡一般可做贷款0-1年的信用分析,B卡则是在申请人有了一定行为后,有了较大数据进行的分析,一般为3-5年,C卡则对数据要求更大,需加入催收后客户反应等属性数据。现金贷行业通过率10%至30%,首逾15%至40%,坏帐4%至15%不等,相关指标根据不同时期市场环境和企业风控水平浮动。另外,风控不是风险越低越好,而是要控制在一个合理水平,根据不同风险对客户(额度,期限,费率)进行定价,风险管理是手段,盈利最大化才是目的。
不同的评分卡,对数据的要求和所应用的建模方法会不一样。
总结下风控机审打分模型建立与分析流程:
项目流程
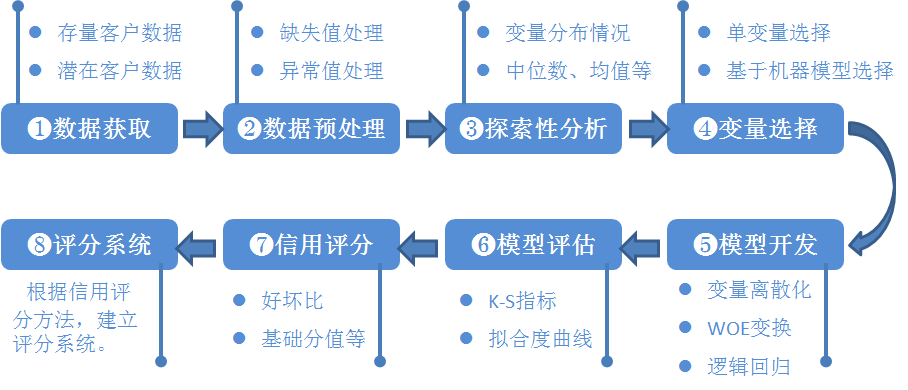
典型的信用评分模型如图1-1所示。信用风险评级模型的主要开发流程如下:
(1) 数据获取,包括获取存量客户及潜在客户的数据。存量客户是指已经在证券公司开展相关融资类业务的客户,包括个人客户和机构客户;潜在客户是指未来拟在证券公司开展相关融资类业务的客户,主要包括机构客户,这也是解决证券业样本较少的常用方法,这些潜在机构客户包括上市公司、公开发行债券的发债主体、新三板上市公司、区域股权交易中心挂牌公司、非标融资机构等。
(2) 数据预处理,主要工作包括数据清洗、缺失值处理、异常值处理,主要是为了将获取的原始数据转化为可用作模型开发的格式化数据。
(3) 探索性数据分析,该步骤主要是获取样本总体的大概情况,描述样本总体情况的指标主要有直方图、箱形图等。
(4) 变量选择,该步骤主要是通过统计学的方法,筛选出对违约状态影响最显著的指标。主要有单变量特征选择方法和基于机器学习模型的方法 。
(5) 模型开发,该步骤主要包括变量分段、变量的WOE(证据权重)变换和逻辑回归估算三部分。
(6) 模型评估,该步骤主要是评估模型的区分能力、预测能力、稳定性,并形成模型评估报告,得出模型是否可以使用的结论。
(7) 信用评分,根据逻辑回归的系数和WOE等确定信用评分的方法。将Logistic模型转换为标准评分的形式。
(8) 建立评分系统,根据信用评分方法,建立自动信用评分系统。
一、 数据准备
数据方面包含借款申请人填写的基本资料,通讯录,通话记录和其他运营商数据,以及在其他第三方平台提供的黑名单和其他借贷平台借贷还款数据,和app抓取的手机数据,有些还包含人行征信,社保公积金工资银行流水等数据,针对不同额度和客群需要用户填写和授权的资料不一样。
收集需要的数据后,通过SQL提取相关变量特征构造建模用的宽表。

二、数据预处理
主要工作包括数据清洗、缺失值处理、异常值处理,主要是为了将获取的原始数据转化为可用作模型开发的格式化数据。
三、变量分析
该步骤主要是获取样本总体的大概情况,描述样本总体情况的指标主要有直方图、箱形图等。
单变量的分布要大致呈正态分布,才能够满足后续分析的条件。多变量之间的相关性要尽可能低。
检查完后切分数据集,将训练数据切分,用于检验
四、模型开发
模型方法常见的有逻辑回归和决策树等,在信用评分卡中一般使用逻辑回归作为主要的模型。过程主要包括变量分箱、变量的WOE(证据权重)变换和变量选择(IV值)、逻辑回归估算。
(1)分类数据根据类别进行WOE变换,连续数据要先进行变量分箱再进行WOE变换。
(2)特征处理阶段主要有两个概念:WOE和IV。
WOE(Weight of Evidence)
即证据权重,WOE是对原始自变量的一种编码形式。要对一个变量进行WOE编码,需要首先把这个变量进行分箱处理(也叫离散化、分箱等等,说的都是一个意思)。
分组后,对于第i组,WOE的计算公式如下:

其中,pyi是这个组中坏客户(此处风险模型中判别的是好坏客户)占所有样本中所有坏客户的比例,pni是这个组中好客户占样本中所有好客户的比例,#yi是这个组中坏客户的数量,#ni是这个组中好客户的数量,#yT是样本中所有坏客户的数量,#nT是样本中所有好客户的数量。
从这个公式中我们可以体会到,WOE表示的实际上是“当前分组中坏客户占所有坏客户的比例”和“当前分组中好客户占所有好客户的比例”的差异。
对这个公式做一个简单变换,可以得到:

变换以后我们可以看出,WOE也可以这么理解,他表示的是当前这个组中坏客户和好客户的比值,和所有样本中这个比值的差异。这个差异是用这两个比值的比值,再取对数来表示的。WOE越大,这种差异越大,这个分组里的样本是坏客户的可能性就越大,WOE越小,差异越小,这个分组里的样本是坏客户的可能性就越小。
WOE的基本特点:
a、当前分组中,坏客户的比例越大,WOE值越大;
b、当前分组WOE的正负,由当前分组坏用户和好用户的比例,与样本整体是坏用户和好用户的比例的大小关系决定。当前分组的比例小于样本整体比例时,WOE为负,变量当前取值对判断个体是否是坏用户起到的负向的影响;当前分组的比例大于整体比例时,WOE为正,变量当前取值对判断个体是否是坏用户起到的正向的影响;当前分组的比例和整体比例相等时,WOE为0。
分箱策略:进行分箱操作时,一般会按每个变量的个数平均分箱,一般设置3~5组,平均分箱之后,为了更好的适应逻辑回归模型,再进一步微调分段范围使woe值尽可能的保持单调性,保持单调性可以使连续数据转化为离散时数据之间能有一定的联系和趋势而不是孤立的几个数据(另外单调从系数的正负上也反映的单变量对结果的影响趋势),当然woe不一定要完全递增或者递减,符合逻辑事实即可。另外对于无法平均分箱的变量,比如说存在一个数值占比很高,可以直接参考woe单调性进行分箱。
IV (Information Value)
信息价值或信息量,用来衡量自变量的预测能力。
在用逻辑回归、决策树等模型方法构建分类模型时,经常需要对自变量进行筛选。挑选入模变量过程需要考虑的因素很多,比如:变量的预测能力,变量之间的相关性,变量的简单性(容易生成和使用),变量的强壮性(不容易被绕过),变量在业务上的可解释性(被挑战时可以解释的通)等等。其中最主要的衡量标准是变量的预测能力。
通过IV去衡量变量预测能力:假设在一个分类问题中,目标变量的类别有两类:Y1,Y2。对于一个待预测的个体A,要判断A属于Y1还是Y2,我们是需要一定的信息的,假设这个信息总量是I,而这些所需要的信息,就蕴含在所有的自变量C1,C2,C3,……,Cn中,那么,对于其中的一个变量Ci来说,其蕴含的信息越多,那么它对于判断A属于Y1还是Y2的贡献就越大,Ci的信息价值就越大,Ci的IV就越大,它就越应该进入到入模变量列表中。其中计算IV值需要先求出WOE值。
IV值,计算公式如下:

有了一个变量各分组的IV值,我们就可以计算整个变量的IV值,方法很简单,就是把各分组的IV相加:

其中,n为变量分组个数。
IV的特点:
a、对于变量的一个分组,这个分组的好用户和坏用户的比例与样本整体响应和未响应的比例相差越大,IV值越大,否则,IV值越小;
b、极端情况下,当前分组的好用户和坏用户的比例和样本整体的好用户和坏用户的比例相等时,IV值为0;
c、IV值的取值范围是[0,+∞),且,当当前分组中只包含好用户或者坏用户时,IV = +∞。
IV值判断变量预测能力的标准
< 0.02: unpredictive,0.02 to 0.1: weak,0.1 to 0.3: medium,0.3 to 0.5: strong,>0.5: suspicious,一般选取大于0.02的
解析下IV计算公式中的(pyi-pni)
假设我们上面所说的营销响应模型中,还有一个变量A,其取值只有两个:0,1,数据如下:

从上表可以看出,当变量A取值1时,其响应比例达到了90%,非常的高,但是我们能否说变量A的预测能力非常强呢?不能。为什么呢?原因就在于,A取1时,响应比例虽然很高,但这个分组的客户数太少了,占的比例太低了。虽然,如果一个客户在A这个变量上取1,那他有90%的响应可能性,但是一个客户变量A取1的可能性本身就非常的低。所以,对于样本整体来说,变量的预测能力并没有那么强。我们分别看一下变量各分组和整体的WOE,IV。

从这个表我们可以看到,变量取1时,响应比达到90%,对应的WOE很高,但对应的IV却很低,原因就在于IV在WOE的前面乘以了一个系数,而这个系数取绝对值可以近似看做是这个分组中样本数占整体样本数的大小,这个系数越小,分组数据对预测起的作用就越小。
总结
WOE其实描述了变量当前这个分组,对判断个体是否是坏用户(分子是坏用户)所起到影响方向和大小,当WOE为正时,变量当前取值对判断个体是否是坏用户起到的正向的影响,当WOE为负时,起到了负向影响。而WOE值的大小,则是这个影响的大小的体现。
IV由于乘以系数(pyi-pni),所以没有了影响方向,只是通过大小反映变量对预测结果的贡献大小,即衡量自变量的预测能力。
(3)利用以上的基础,通过IV选择变量,将自变量中的值替换成对应分组的woe值
(4)逻辑回归估算:将替换成woe数值之后的变量作为训练数据,使用逻辑回归算法将借款人特征转化为一个标准的评分卡。当输入这些变量的具体值的时候,可以得到相应的分数。
风控分类的主要模型:


其中主要用到的算法有:

五、模型评估
该步骤主要是评估模型的预测f分辨能力(ROC/AUC 、K-S值、GINI系数)、稳定性(PSI),并形成模型评估报告,得出模型是否可以使用的结论。
(1)ROC(receiver operating characteristic curve)
ROC全称是“受试者工作特征”(Receiver Operating Characteristic)。ROC曲线的面积就是AUC(Area Under the Curve)。AUC用于衡量“二分类问题”机器学习算法性能。
首先看下python中评估的sklearn函数
分类模型评估:

混淆矩阵,假设有一批test样本,这些样本只有两种类别:正例和反例。机器学习算法预测类别如下图(左半部分预测类别为正例,右半部分预测类别为反例),而样本中真实的正例类别在上半部分,下半部分为真实的反例。

预测值为正例,记为P(Positive)
预测值为反例,记为N(Negative)
预测值与真实值相同,记为T(True)
预测值与真实值相反,记为F(False)
TP:预测类别是P(正例),真实类别也是P
FP:预测类别是P,真实类别是N(反例)
TN:预测类别是N,真实类别也是N
FN:预测类别是N,真实类别是P
TP+FP=P
FN+TN=N
TP+TN=T
FP+FN=F
决策类评估——混淆矩阵指标:
正确率(Accuracy Rate):(TP+TN)/(P+N)。
召回率(灵敏度,TPR,True Positive Rate):TP/(TP+FN)。在所有实际是正样本中有多少被正确识别为正样本。
查准率(命中率,Precision Rate):TP/P。被识别成正样本的样本中有多少是真的正样本。欺诈分析中,命中率(不低于20%),看模型预测识别的能力。
误报率(FPR,False Positive Rate):FP/(FP+TN)。在所有实际为负样本中有多少被错误识别为正样本。
排序类评估——ROC指标:
还有一个概念叫”截断点”。机器学习算法对test样本进行预测后,可以输出各test样本对某个类别的相似度概率。比如t1是P类别的概率为0.3,一般我们认为概率低于0.5,t1就属于类别N。这里的0.5,就是”截断点”。
总结一下,对于计算ROC,最重要的三个概念就是TPR, FPR, 截断点。
截断点取不同的值,TPR和FPR的计算结果也不同。将截断点不同取值下对应的TPR和FPR结果画于二维坐标系中得到的曲线,就是ROC曲线。横轴用FPR表示,以TPR为纵坐标,而曲线下方的面积就是AUC(Area Under Curve)。
ROC曲线,比如图中的A点。A点对应的是,给定一个划分好坏客户的分数线(比如600分以上是好人),然后使用这个模型进行预测。预测的结果是,实际上为坏客户且预测结果是坏客户的概率是0.8,而实际是好客户却被预测为坏客户的概率是0.1。由于我们可以设定不同的分数线,因此通过这种方式可以产生不同的点,这些点也就连成了ROC曲线。

按照上面的理解,那我们肯定希望被准确预测为坏人的概率越高越好,而被误判为好人的概率越低越好,所以一个越好的分类模型,ROC曲线越接近左上方,AUC也越来越接近1;反之,如果这个分类模型得出的结果基本上相当于随机猜测,那么画出的图像就很接近于左下角和右上角的对角线(即图中标注的“random chance”),那么这个模型也就没什么意义了。

AUC=A+C
(2)K-S值

在完成一个模型后,将测试模型的样本平均分成10组,以好样本占比降序从左到右进行排列,其中第一组的好样本占比最大,坏样本占比最小。这些组别的好坏样本占比进行累加后得到每一组对应的累计的占比。好坏样本的累计占比随着样本的累计而变化(图中Good/Bad两条曲线),而两者差异最大时就是我们要求的K-S值
KS值的取值范围是[0,1]。通常来说,值越大,表明正负样本区分的程度越好。一般,KS值>0.2就可认为模型有比较好的预测准确性。
(3)GINI系数

使用洛伦茨曲线,可以描述预期违约客户的分布。
对于基尼系数,例如将一个国家所有的人口按最贫穷到最富有进行排列,随着人数的累计,这些人口所拥有的财富的比例也逐渐增加到100%,按这个方法得到图中的曲线,称为洛伦兹曲线。基尼系数就是图中A/B的比例。可以看到,假如这个国家最富有的那群人占据了越多的财富,贫富差距越大,那么洛伦茨曲线就会越弯曲,基尼系数就越大。
同样的,假设我们把100个人的信用评分按照从高到低进行排序,以横轴为累计人数比例,纵轴作为累计坏样本比例,随着累计人数比例的上升,累计坏样本的比例也在上升。如果这个评分的区分能力比较好,那么越大比例的坏样本会集中在越低的分数区间,整个图像形成一个凹下去的形状。所以洛伦兹曲线的弧度越大,基尼系数越大,这个模型区分好坏样本的能力就越强。
在ROC图中,GINI=A/(A+B)=A/C=(A+C)/C-1=AUC/C-1
其中,C=1/2 所以,GINI=2AUC-1
(4)PSI
群体稳定性指标(population stability index),
公式: psi = sum((实际占比-预期占比)* ln(实际占比/预期占比))
举个例子解释下,比如训练一个logistic回归模型,预测时候会有个概率输出p。你测试集上的输出设定为p1吧,将它从小到大排序后10等分,如0-0.1,0.1-0.2,......。
现在用这个模型去对新的样本进行预测,预测结果叫p2,按p1的区间也划分为10等分。
实际占比就是p2上在各区间的用户占比,预期占比就是p1上各区间的用户占比。
意义就是如果模型跟稳定,那么p1和p2上各区间的用户应该是相近的,占比不会变动很大,也就是预测出来的概率不会差距很大。
一般认为psi小于0.1时候模型稳定性很高,0.1-0.25一般,大于0.25模型稳定性差,建议重做。
六、模型监控
模型监控与模型效果评测一样,也是从两个方面去监控,一是有效性,主要看过件样本在后续的逾期表现,这种逾期不需要和建模样本那么严格,可以放松一些。二是稳定性,同样是变量稳定性和模型稳定性,评测的方式与模型效果评价部分类似。监测可以分为前端、后端监控。

(1)前端监控,授信之前,别的客户来了,这个模型能不能用?
长期使用的模型,其中的变量一定不能波动性较大。
比如,收入这个指标,虽然很重要,但是波动性很大,不适合用在长期建模过程中。如果硬要把收入放到模型之中,可以改成收入的百分位制(排名)。
(2)后端监控,建模授信之后,打了分数,看看一年之后,分数是否发生了改变。
主要监控模型的正确性以及变量选择的有效性。出现了不平滑的问题,需要重新考虑

接下来会基于python进行信用评分模型的模型开发、模型评估和信用评分等。
https://zhuanlan.zhihu.com/p/31229720
https://www.jianshu.com/p/f931a4df202c
https://blog.csdn.net/jiabiao1602/article/details/77869524
https://blog.csdn.net/shenxiaoming77/article/details/72627882/
https://www.zhihu.com/question/24490261
https://www.jianshu.com/p/c03de958099a
https://blog.csdn.net/sinat_26917383/article/details/51725102
https://www.sohu.com/a/164097017_305272
https://www.zhihu.com/question/37405102/answers/created