MUTC 3 D Cut the cake 最大子矩阵

Cut the cake

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 835    Accepted Submission(s): 308

Problem Description

Mark bought a huge cake, because his friend ray_sun’s birthday is coming. Mark is worried about how to divide the cake since it’s so huge and ray_sun is so strange. Ray_sun is a nut, you can never imagine how strange he was, is, and going to be. He does not eat rice, moves like a cat, sleeps during work and plays games when the rest of the world are sleeping……It is not a surprise when he has some special requirements for the cake. A considering guy as Mark is, he will never let ray_sun down. However, he does have trouble fulfilling ray_sun’s wish this time; could you please give him a hand by solving the following problem for him?
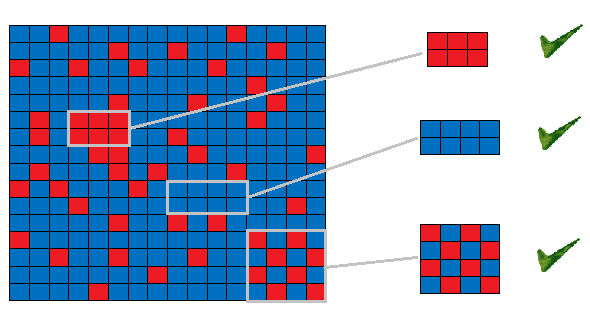
  The cake can be divided into n*m blocks. Each block is colored either in blue or red. Ray_sun will only eat a piece (consisting of several blocks) with special shape and color. First, the shape of the piece should be a rectangle. Second, the color of blocks in the piece should be the same or red-and-blue crisscross. The so called ‘red-and-blue crisscross’ is demonstrated in the following picture. Could you please help Mark to find out the piece with maximum perimeter that satisfies ray_sun’s requirements?

 

Input

The first line contains a single integer T (T <= 20), the number of test cases.
  For each case, there are two given integers, n, m, (1 <= n, m <= 1000) denoting the dimension of the cake. Following the two integers, there is a n*m matrix where character B stands for blue, R red.

 

Output

For each test case, output the cased number in a format stated below, followed by the maximum perimeter you can find.

 

Sample Input

2
1 1
B
3 3
BBR
RBB
BBB

 

Sample Output

Case #1: 4
Case #2: 8

 

Author

BJTU

 

Source

2012 Multi-University Training Contest 3

 

Recommend

zhoujiaqi2010

 

---------------

扫描线法求最大子矩阵

---------------

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int maxn=1111;

int mat[maxn][maxn];
int n,m;

//返回矩形的最大面积，障碍物代号为c
int cat(int c)
{
    int h[maxn],l[maxn],r[maxn];
    int lo,ro;
    int ans=0;
    for (int j=1;j<=m;j++)
    {
        h[j]=0;
        l[j]=1;
        r[j]=m;
    }
    for (int i=1;i<=n;i++)
    {
        lo=0;ro=m+1;
        for (int j=1;j<=m;j++)
        {
            if (mat[i][j]==c){ h[j]=0;l[j]=1;lo=j; }
            else
            {
                h[j]++;
                l[j]=max(l[j],lo+1);
            }
        }
        for (int j=m;j>=1;j--)
        {
            if (mat[i][j]==c){ r[j]=m;ro=j; }
            else
            {
                r[j]=min(r[j],ro-1);
                ans=max(ans,(h[j]+(r[j]-l[j]+1))*2);
            }
        }
    }
    return ans;
}

char s[maxn][maxn];

int main()
{
    int T;
    int ans;
    int cnt=0;
    scanf("%d",&T);
    while (T--)
    {
        ans=0;
        scanf("%d%d",&n,&m);
        for (int i=1;i<=n;i++)
        {
            scanf("%s",s[i]+1);
        }
        for (int i=1;i<=n;i++)
        {
            for (int j=1;j<=m;j++)
            {
                if (s[i][j]=='B') mat[i][j]=0;
                if (s[i][j]=='R') mat[i][j]=1;
            }
        }
        ans=max(ans,cat(1));
        ans=max(ans,cat(0));
        for (int i=1;i<=n;i++)
        {
            for (int j=1;j<=m;j++)
            {
                if ((i+j)%2==0)
                {
                    mat[i][j]^=1;
                }
            }
        }
        ans=max(ans,cat(1));
        ans=max(ans,cat(0));
        printf("Case #%d: %d\n",++cnt,ans);
    }
    return 0;
}