问题描述
将n块电路板以最佳排列方式插入带有n个插槽的机箱中。n块电路板的不同排列方式对应于不同的电路板插入方案。设B={1, 2, …, n}是n块电路板的集合,集合L={N1, N2, …, Nm}是连接这n块电路板中若干电路板的m个连接块。其中,每个连接块Ni是B的一个子集,且Ni中的电路板用同一条导线连接在一起。设x表示n块电路板的一个排列,即在机箱的第i个插槽中插入的电路板编号是x[i]。x所确定的电路板排列Density (x)密度定义为跨越相邻电路板插槽的最大连线数。
例:如图,设n=8, m=5,给定n块电路板及其m个连接块:B={1, 2, 3, 4, 5, 6, 7, 8},L={N1,N2,N3,N4,N5},N1={4, 5, 6},N2={2, 3},N3={1, 3},N4={3, 6},N5={7, 8};其中可能的排列如图所示,则该电路板排列的密度是2。
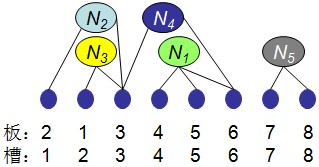
上图中,跨越插槽2和3,4和5,以及插槽5和6的连线数均为2。插槽6和7之间无跨越连线。其余插槽之间只有1条跨越连线。在设计机箱时,插槽一侧的布线间隙由电路板的排列的密度确定。因此,电路板排列问题要求对于给定的电路板连接条件(连接块),确定电路板的最佳排列,使其具有最小密度。
问题分析
电路板排列问题是NP难问题,因此不大可能找到解此问题的多项式时间算法。考虑采用回溯法系统的搜索问题解空间的排列树,找出电路板的最佳排列。算法中用整型数组B表示输入。B[i][j]的值为1当且仅当电路板i在连接块Nj中。设total[j]是连接块Nj中的电路板数。对于电路板的部分排列x[1:i],设now[j]是x[1:i]中所包含的Nj中的电路板数。由此可知,连接块Nj的连线跨越插槽i和i+1当且仅当now[j]>0且now[j]!=total[j]。用这个条件来计算插槽i和i+1间的连线密度。
算法具体实现如下:

//电路板排列问题 回溯法求解 #include "stdafx.h" #include <iostream> #include <fstream> using namespace std; ifstream fin("5d11.txt"); class Board { friend int Arrangement(int **B, int n, int m, int bestx[]); private: void Backtrack(int i,int cd); int n, //电路板数 m, //连接板数 *x, //当前解 *bestx,//当前最优解 bestd, //当前最优密度 *total, //total[j]=连接块j的电路板数 *now, //now[j]=当前解中所含连接块j的电路板数 **B; //连接块数组 }; template <class Type> inline void Swap(Type &a, Type &b); int Arrangement(int **B, int n, int m, int bestx[]); int main() { int m = 5,n = 8; int bestx[9]; //B={1,2,3,4,5,6,7,8} //N1={4,5,6},N2={2,3},N3={1,3},N4={3,6},N5={7,8} cout<<"m="<<m<<",n="<<n<<endl; cout<<"N1={4,5,6},N2={2,3},N3={1,3},N4={3,6},N5={7,8}"<<endl; cout<<"二维数组B如下:"<<endl; //构造B int **B = new int*[n+1]; for(int i=1; i<=n; i++) { B[i] = new int[m+1]; } for(int i=1; i<=n; i++) { for(int j=1; j<=m ;j++) { fin>>B[i][j]; cout<<B[i][j]<<" "; } cout<<endl; } cout<<"当前最优密度为:"<<Arrangement(B,n,m,bestx)<<endl; cout<<"最优排列为:"<<endl; for(int i=1; i<=n; i++) { cout<<bestx[i]<<" "; } cout<<endl; for(int i=1; i<=n; i++) { delete[] B[i]; } delete[] B; return 0; } void Board::Backtrack(int i,int cd)//回溯法搜索排列树 { if(i == n) { for(int j=1; j<=n; j++) { bestx[j] = x[j]; } bestd = cd; } else { for(int j=i; j<=n; j++) { //选择x[j]为下一块电路板 int ld = 0; for(int k=1; k<=m; k++) { now[k] += B[x[j]][k]; if(now[k]>0 && total[k]!=now[k]) { ld ++; } } //更新ld if(cd>ld) { ld = cd; } if(ld<bestd)//搜索子树 { Swap(x[i],x[j]); Backtrack(i+1,ld); Swap(x[i],x[j]); //恢复状态 for(int k=1; k<=m; k++) { now[k] -= B[x[j]][k]; } } } } } int Arrangement(int **B, int n, int m, int bestx[]) { Board X; //初始化X X.x = new int[n+1]; X.total = new int[m+1]; X.now = new int[m+1]; X.B = B; X.n = n; X.m = m; X.bestx = bestx; X.bestd = m+1; //初始化total和now for(int i=1; i<=m; i++) { X.total[i] = 0; X.now[i] = 0; } //初始化x为单位排列并计算total for(int i=1; i<=n; i++) { X.x[i] = i; for(int j=1; j<=m; j++) { X.total[j] += B[i][j]; } } //回溯搜索 X.Backtrack(1,0); delete []X.x; delete []X.total; delete []X.now; return X.bestd; } template <class Type> inline void Swap(Type &a, Type &b) { Type temp=a; a=b; b=temp; }
实现结果: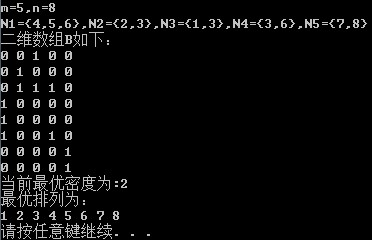
算法效率:
在解空间排列树的每个节点处,算法Backtrack花费O(m)计算时间为每个儿子节点计算密度。因此计算密度所消耗的总计算时间为O(mn!)。另外,生成排列树需要O(n!)时间。每次更新当前最优解至少使bestd减少1,而算法运行结束时bestd>=0。因此最优解被更新的额次数为O(m)。更新最优解需要O(mn)时间。综上,解电路板排列问题的回溯算法Backtrack所需要的计算时间为O(mn!)。
转载:https://blog.csdn.net/liufeng_king/article/details/8898372
