[刷题] 0-1背包问题

要求

• 背包容量为C，现有n种不物品，编号为0...n-1，每件物品重量为w(i)，价值为v(i)
• 在不超过背包容量基础上，如何放物品，使得物品总价值最大

思路

• 暴力：每件物品都可以放进或不放进背包（(2^n)*n）
• 贪心：优先放入平均价值最高的物品（可能导致空间浪费，不是全局最优解）

实现

• 状态：F(n,C)，将n个物品放入容量为C的背包，使得价值最大
• 状态转移：第 i 个物品放入（12） / 不放入背包（10），使得价值最大
• 第 i 个物品放入背包时，首先保证有足够空间能放入，再用剩余空间放其他物品
• F(i,c) = max(F(i-1,c) , v(i)+F(i-1,c-w(i)))

递归

class Knapsack01{
    // w：物品重量，v：物品价值 
    // 用[0...index]的物品，填充容积为c的背包的最大价值 
    private:
        int bestValue(const vector<int> &w, const vector<int> &v, int index, int c){
            
            if( index < 0 || c <= 0 )
                return 0;
                
            int res = bestValue(w, v, index-1, c );
            if( c >= w[index] )
                res = max(res, v[index] + bestValue(w, v, index-1, c-w[index]));
            
            return res;
        }
    
    public:
        int knapsack01(const vector<int> &w, const vector<int> &v, int C){
            
            int n = w.size();
            // 0...n-1的物品装入容积为C的背包 
            return bestValue( w, v, n-1, C);
        }
    
};

记忆化搜索

class Knapsack01{
    // w：物品重量，v：物品价值 
    // 用[0...index]的物品，填充容积为c的背包的最大价值 
    private:
        int bestValue(const vector<int> &w, const vector<int> &v, int index, int c){
            
            if( index < 0 || c <= 0 )
                return 0;
            
            if( memo[index][c] != -1)
                return memo[index][c];
                    
            int res = bestValue(w, v, index-1, c );
            if( c >= w[index] )
                res = max(res, v[index] + bestValue(w, v, index-1, c-w[index]));
            memo[index][c] = res;
            return res;
        }
    
    public:
        int knapsack01(const vector<int> &w, const vector<int> &v, int C){
            
            int n = w.size();
            memo = vector<vector<int>>(n, vector<int>(C+1, -1));
            // 0...n-1的物品装入容积为C的背包 
            return bestValue( w, v, n-1, C);
        }
    
};

动态规划

• 行：物品个数（i）
• 列：背包容量（j）
• 每次取放入 / 不放入新物品的最大值
• 12-13：填写第一行

 3个物品，背包容积为5

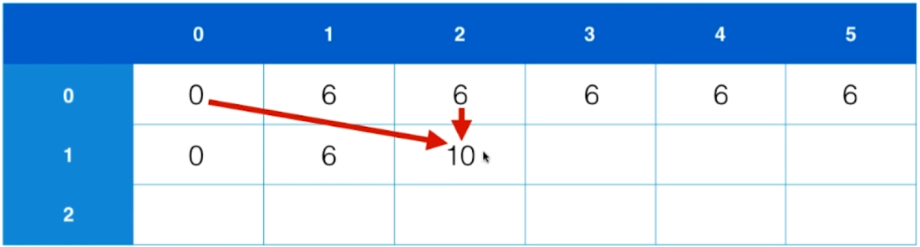背包容积为2，max(6,0+10)=10

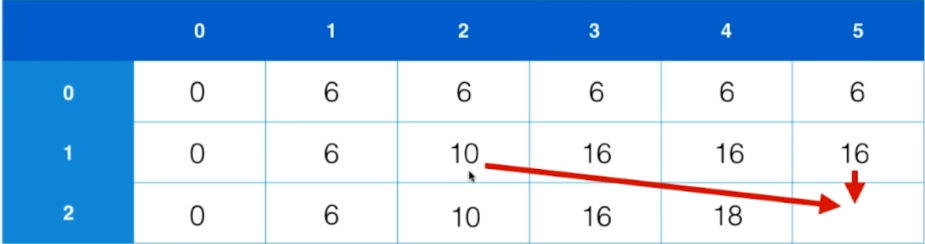 背包容积为5，max(16,10+12)=22

class Knapsack01{
    public:
        int knapsack01(const vector<int> &w, const vector<int> &v, int C){
            
            assert( w.size() == v.size() );
            int n = w.size();
            if( n == 0 )
                return 0;
                
            vector<vector<int>> memo( n, vector<int>(C+1,-1));
            
            for( int j = 0 ; j <= C ; j ++ )
                memo[0][j] = ( j >= w[0] ? v[0] : 0 );
            
            for( int i = 1 ; i < n ; i ++ )
                for( int j = 0 ; j <= C ; j ++ ){
                    memo[i][j] = memo[i-1][j];
                    if( j >= w[i] )
                        memo[i][j] = max( memo[i][j] , v[i] + memo[i-1][j-w[i]] )
                }
            return memo[n-1][C];
        }
};

优化

• 原方法：时间（n*C），空间（n*C）
• 第 i 行元素只依赖于第 i-1 行元素，故只需保存两行元素，空间（2*C）

class Knapsack01{
    public:
        int knapsack01(const vector<int> &w, const vector<int> &v, int C){
            
            assert( w.size() == v.size() );
            int n = w.size();
            if( n == 0 )
                return 0;
                
            vector<vector<int>> memo( 2, vector<int>(C+1,-1));
            
            for( int j = 0 ; j <= C ; j ++ )
                memo[0][j] = ( j >= w[0] ? v[0] : 0 );
            
            for( int i = 1 ; i < n ; i ++ )
                for( int j = 0 ; j <= C ; j ++ ){
                    memo[i%2][j] = memo[(i-1)%2][j];
                    if( j >= w[i] )
                        memo[i%2][j] = max( memo[i%2][j] , v[i] + memo[(i-1)%2][j-w[i]] )
                }
            return memo[(n-1)%2][C];
        }
};

• 进一步优化，只用一行，从右向左更新，空间（C）

  6->16

class Knapsack01{
    public:
        int knapsack01(const vector<int> &w, const vector<int> &v, int C){
            
            assert( w.size() == v.size() );
            int n = w.size();
            if( n == 0 || C == 0)
                return 0;
                
            vector<int> memo( C+1,-1 );
            
            for( int j = 0 ; j <= C ; j ++ )
                mem[j] = ( j >= w[0] ? v[0] : 0 );
            
            for( int i = 1 ; i < n ; i ++ )
                for( int j = C ; j >= w[i] ; j -- )
                    memo[j] = max( memo[j] , v[i] + memo[j-w[i]] )
            return memo[C];
        }
};

变种

• 完全背包问题：每个物品可以无限使用
• 多重背包问题：每个物品有num[i]个
• 多维费用背包问题：考虑物品体积和重量两个维度
• 物品间加入约束的背包问题：物品间相互排斥/依赖