哈夫曼树

1. 概念

哈夫曼树是一个特殊的二叉树，它的特殊在于：

• 叶子节点带有权值：对叶子结点赋予的一个有意义的数值量
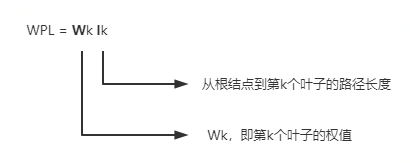
• 二叉树的带权路径长度：设二叉树具有n个带权值的叶子结点，从根结点到各个叶子结点的路径长度与相应叶子结点权值的乘积之和。记为 WPL=Wklk，这里的WPL即带权路径长度（Weight Path Length）。
• 权值越大的叶子结点越靠近根结点，而权值越小的叶子结点越远离根结点
• 只有度为0的叶子结点和度为2的分支节点，不存在度为1的结点
  
  综上，总结哈夫曼树的概念为：

哈夫曼树：给定一组具有确定权值的叶子节点，带权路径长度最小的二叉树

举例：给定4个叶子结点，其权值分别为{2,3,4,7}，可以构造出形状不同的多个二叉树。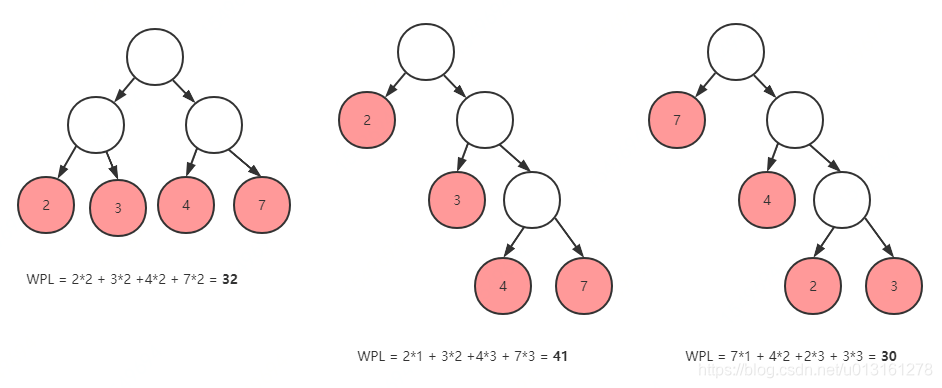

如上图所示，可以根据给定的叶子结点构建出不同的二叉树结构，按照计算以上三个二叉树带权路径长度计算公式得出的WPL分别为32、41、30，根据哈夫曼树定义可知，最右侧WPL=30的这个二叉树就是一个哈夫曼树。

2. 基本思想

2.1 初始化

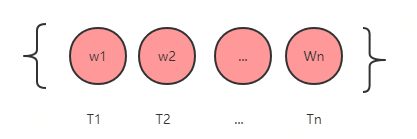
由给定的n个权值 {w1,w2,…,wn} 构造n颗只有一个根结点的二叉树，从而得到一个二叉树集合F= {T1,T2,…,Tn}

2.2 选取与合并

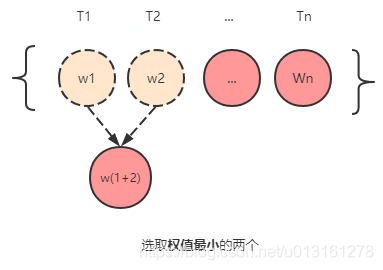
在集合F中选取根结点的权值最小的两颗二叉树分别作为左、右子树构造一颗新的二叉树，这颗二叉树的根结点的权值为其左、右子树根结点的权值之和

2.3 删除与加入

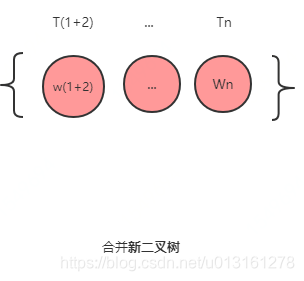
在集合F中删除作为作为左、右子树的两颗二叉树，并将新建立的二叉树加入到集合F中

2.4 递归

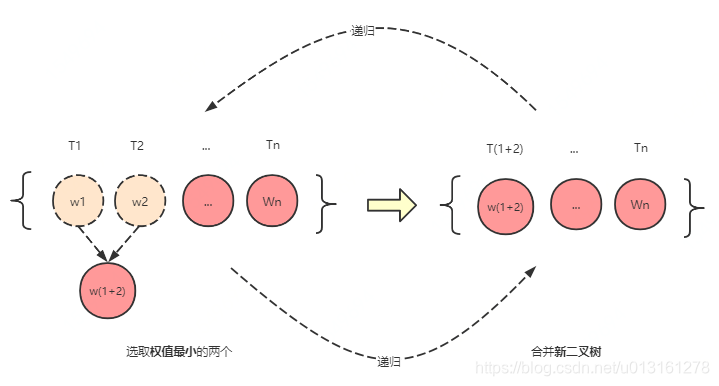
重复以上选取与合并、删除与加入两步，当集合F中只剩下一颗二叉树时，这颗二叉树便是哈夫曼树

2.5 实例

我们按照上面的例子，初始化集合{2,3,4,7}来模拟下哈夫曼树的推演过程，记录如下：

3. 数据结构

设置一个数组 huffTree 来存储哈夫曼树中各结点信息，数组元素的数据结构如下图：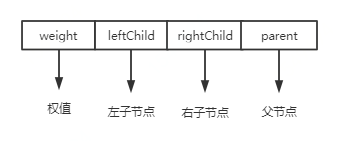

• weight 权值
• leftChild 左子节点，存储数组下标
• rightChild 右子节点，存储数组下标
• parent 父节点，存储数组下标

数组大小可以通过2n-1来计算获得，为何是2n-1大小，可以参考二叉树性质来计算。

根据上面的初始化、选取与合并、删除与加入、递归的步骤方法推演，进行数组操作过程如下：

4. 代码实现

参考的资料中是采用朴素的数组进行存储的，数组存储的困难在于不利于动态扩容和调整，这里采用List集合进行存储，实际上底层也是数组存储，只是通过封装好的容器进行调用即可。这里还是延用上面图例中的权值数组 {2,3,4,7}，除此之外，还可以使用 {2,3,5,7,5} 这种新构建结点等于已存在权值结点、多个权值结点权值相等各种特殊情况来进行验证。

/**
 * 哈夫曼树
 * created by guanjian on 2020/12/30 15:43
 */
public class HuffmanTree {

    //权值结点
    private Integer[] weightArray;
    //哈夫曼树结点总数 2*weights - 1
    private int huffmanTreeNodeLength;
    //哈夫曼树结点数组
    private List<HuffmanTreeNode> huffmanTreeNodeList;
    //每次获取最小权值数量
    private final static int minNodeLength = 2;

    public HuffmanTree(Integer[] weightArray) {
        Assert.notEmpty(weightArray, "weightArray can not be empty");
        this.weightArray = weightArray;
    }

    /**
     * 初始化哈夫曼树结点数组
     */
    public void initHuffmanTreeNodeArray() {
        //哈夫曼树结点总数 2*weights - 1
        this.huffmanTreeNodeLength = 2 * this.weightArray.length - 1;
        this.huffmanTreeNodeList = Lists.newArrayListWithCapacity(huffmanTreeNodeLength);

        //初始化填充哈夫曼树结点
        IntStream.range(0, weightArray.length).forEach(i -> {
            //这里将权值灌入到node节点中
            huffmanTreeNodeList.add(
                    HuffmanTreeNode.Builder.aHuffmanTreeNode()
                            .weight(weightArray[i])
                            .build()
            );
        });
        System.out.format("初始化完成 huffmanTreeNodeList=%s 
", Arrays.toString(huffmanTreeNodeList.toArray()));
    }

    /**
     * 查找最小权值方法
     */
    public List<HuffmanTreeNode> findMinNodes() {
        //按权值从小到大升序进行排序
        List<HuffmanTreeNode> sortedList = huffmanTreeNodeList.stream()
                .filter(x -> !x.isSorted())
                .sorted(Comparator.comparing(HuffmanTreeNode::getWeight))
                .collect(Collectors.toList());
        sortedList.forEach(x -> System.out.format("排序 %s 处理 %s 
", x.getWeight(), x.isSorted()));
        //取最小权值的两个node
        List<HuffmanTreeNode> list = sortedList.subList(0,
                sortedList.size() >= minNodeLength ? minNodeLength : sortedList.size());

        if (CollectionUtils.isEmpty(list)) return list;

        list.forEach(x -> {
            x.setSorted(true);
        });
        return list;
    }

    /**
     * 构建哈夫曼树
     */
    public void buildHuffmanTree() {
        for (; ; ) {
            /**
             * 选取权值最小的两个结点，构造父节点
             */
            List<HuffmanTreeNode> minNodes = findMinNodes();
            if (minNodes.size() != minNodeLength) break;

            //左子节点
            HuffmanTreeNode leftChild = minNodes.get(0);
            //右子节点
            HuffmanTreeNode rightChild = minNodes.get(1);
            //父结点
            HuffmanTreeNode parent = HuffmanTreeNode.Builder.aHuffmanTreeNode()
                    .weight(leftChild.getWeight() + rightChild.getWeight())
                    .leftChild(leftChild)
                    .rightChild(rightChild)
                    .build();

            leftChild.setParent(parent);
            rightChild.setParent(parent);

            System.out.println("====================================");
            System.out.format("获取左子结点权值=%s
", leftChild.getWeight());
            System.out.format("获取右子结点权值=%s
", rightChild.getWeight());
            System.out.format("获取父结点权值=%s
", parent.getWeight());

            huffmanTreeNodeList.add(parent);
        }
    }

    /**
     * 计算当前二叉树的WPL
     * weight（结点权值） * path（树高度） = WPL（权值路径）
     */
    public void calculateWeightPathLength() {
        System.out.println("====================================");

        int wpl = 0;

        for (HuffmanTreeNode node : huffmanTreeNodeList) {
            //跳过构建结点,只计算权值结点
            if (null != node.leftChild || null != node.rightChild) continue;

            int path = 0;
            HuffmanTreeNode currentNode = node;
            while (null != currentNode.parent) {
                path++;
                currentNode = currentNode.parent;
            }
            System.out.format("权值：%s * 路径长度：%s 
", node.getWeight(), path);
            wpl += node.getWeight() * path;
        }
        System.out.format("WPL=%s 
", wpl);
    }

    public Integer[] getWeightArray() {
        return weightArray;
    }

    public void setWeightArray(Integer[] weightArray) {
        this.weightArray = weightArray;
    }

    public int getHuffmanTreeNodeLength() {
        return huffmanTreeNodeLength;
    }

    public void setHuffmanTreeNodeLength(int huffmanTreeNodeLength) {
        this.huffmanTreeNodeLength = huffmanTreeNodeLength;
    }

    public List<HuffmanTreeNode> getHuffmanTreeNodeList() {
        return huffmanTreeNodeList;
    }

    public void setHuffmanTreeNodeList(List<HuffmanTreeNode> huffmanTreeNodeList) {
        this.huffmanTreeNodeList = huffmanTreeNodeList;
    }

    public static int getMinNodeLength() {
        return minNodeLength;
    }

    static class HuffmanTreeNode {

        /**
         * 父结点
         */
        private HuffmanTreeNode parent;

        /**
         * 左子结点
         */
        private HuffmanTreeNode leftChild;

        /**
         * 右子结点
         */
        private HuffmanTreeNode rightChild;

        /**
         * 权重值
         */
        private int weight;

        /**
         * 是否完成排序
         */
        private boolean sorted;

        public HuffmanTreeNode getParent() {
            return parent;
        }

        public void setParent(HuffmanTreeNode parent) {
            this.parent = parent;
        }

        public HuffmanTreeNode getLeftChild() {
            return leftChild;
        }

        public void setLeftChild(HuffmanTreeNode leftChild) {
            this.leftChild = leftChild;
        }

        public HuffmanTreeNode getRightChild() {
            return rightChild;
        }

        public void setRightChild(HuffmanTreeNode rightChild) {
            this.rightChild = rightChild;
        }

        public int getWeight() {
            return weight;
        }

        public void setWeight(int weight) {
            this.weight = weight;
        }

        public boolean isSorted() {
            return sorted;
        }

        public void setSorted(boolean sorted) {
            this.sorted = sorted;
        }

        public static class Builder {

            private HuffmanTreeNode parent;
            private HuffmanTreeNode leftChild;
            private HuffmanTreeNode rightChild;
            private int weight;
            private boolean sorted;

            private Builder() {
            }

            public static Builder aHuffmanTreeNode() {
                return new Builder();
            }

            public Builder weight(int weight) {
                this.weight = weight;
                return this;
            }

            public Builder parent(HuffmanTreeNode parent) {
                this.parent = parent;
                return this;
            }

            public Builder rightChild(HuffmanTreeNode rightChild) {
                this.rightChild = rightChild;
                return this;
            }

            public Builder leftChild(HuffmanTreeNode leftChild) {
                this.leftChild = leftChild;
                return this;
            }

            public Builder sorted(boolean sorted) {
                this.sorted = sorted;
                return this;
            }

            public HuffmanTreeNode build() {
                HuffmanTreeNode huffmanTreeNode = new HuffmanTreeNode();
                huffmanTreeNode.setLeftChild(this.leftChild);
                huffmanTreeNode.setRightChild(this.rightChild);
                huffmanTreeNode.setParent(this.parent);
                huffmanTreeNode.setWeight(this.weight);
                huffmanTreeNode.setSorted(this.sorted);
                return huffmanTreeNode;
            }
        }

        @Override
        public String toString() {
            return "HuffmanTreeNode{" +
                    "parent=" + parent +
                    ", leftChild=" + leftChild +
                    ", rightChild=" + rightChild +
                    ", weight=" + weight +
                    ", sorted=" + sorted +
                    '}';
        }
    }

    public static void main(String[] args) {
        //权值结点
        Integer[] weightArray = new Integer[]{2,3,4,7};

        //声明哈夫曼树
        HuffmanTree huffmanTree = new HuffmanTree(weightArray);
        //初始化哈夫曼树
        huffmanTree.initHuffmanTreeNodeArray();
        //构建哈夫曼树
        huffmanTree.buildHuffmanTree();
        //WPL
        huffmanTree.calculateWeightPathLength();
    }
}

【控制台输出】
初始化完成 huffmanTreeNodeList=[HuffmanTreeNode{parent=null, leftChild=null, rightChild=null, weight=2, sorted=false}, HuffmanTreeNode{parent=null, leftChild=null, rightChild=null, weight=3, sorted=false}, HuffmanTreeNode{parent=null, leftChild=null, rightChild=null, weight=4, sorted=false}, HuffmanTreeNode{parent=null, leftChild=null, rightChild=null, weight=7, sorted=false}] 
排序 2 处理 false 
排序 3 处理 false 
排序 4 处理 false 
排序 7 处理 false 
====================================
获取左子结点权值=2
获取右子结点权值=3
获取父结点权值=5
排序 4 处理 false 
排序 5 处理 false 
排序 7 处理 false 
====================================
获取左子结点权值=4
获取右子结点权值=5
获取父结点权值=9
排序 7 处理 false 
排序 9 处理 false 
====================================
获取左子结点权值=7
获取右子结点权值=9
获取父结点权值=16
排序 16 处理 false 
====================================
权值：2 * 路径长度：3 
权值：3 * 路径长度：3 
权值：4 * 路径长度：2 
权值：7 * 路径长度：1 
WPL=30 

5. 参考

https://space.bilibili.com/26340287 懒猫老师数据结构讲解

转载：https://blog.csdn.net/u013161278/article/details/111942554?utm_medium=distribute.pc_category.none-task-blog-hot-5.nonecase&depth_1-utm_source=distribute.pc_category.none-task-blog-hot-5.nonecase

https://blog.csdn.net/u013161278/article/details/111942554?utm_medium=distribute.pc_category.none-task-blog-hot-5.nonecase&depth_1-utm_source=distribute.pc_category.none-task-blog-hot-5.nonecase