hdu 5375

Gray code

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 684    Accepted Submission(s): 402

Problem Description

The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only onebit (binary digit). The reflected binary code was originally designed to prevent spurious output from electromechanical switches. Today, Gray codes are widely used to facilitate error correction in digital communications such as digital terrestrial television and some cable TV systems.



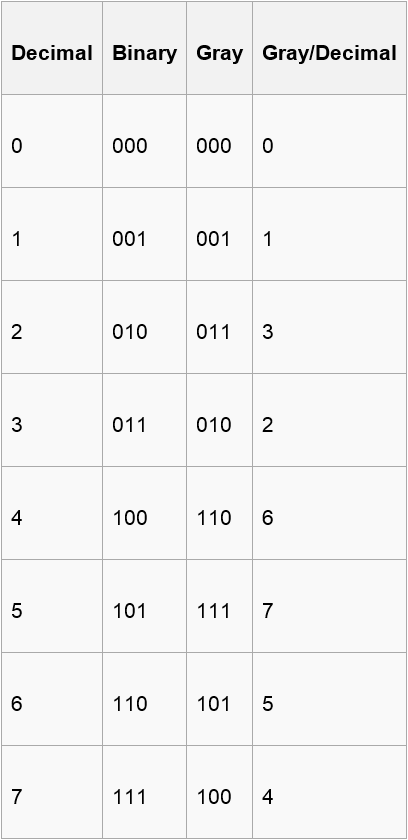
Now , you are given a binary number of length n including ‘0’ , ’1’ and ‘?’(?

means that you can use either 0 or 1 to fill this position) and n integers(a1,a2,….,an) . A certain binary number corresponds to a gray code only. If the ith bit of this gray code is 1,you can get the point ai.
Can you tell me how many points you can get at most?

For instance, the binary number “00?

0” may be “0000” or “0010”,and the corresponding gray code are “0000” or “0011”.You can choose “0000” getting nothing or “0011” getting the point a3 and a4.

 

Input

The first line of the input contains the number of test cases T.

Each test case begins with string with ‘0’,’1’ and ‘?’.

The next line contains n (1<=n<=200000) integers (n is the length of the string).

a1 a2 a3 … an (1<=ai<=1000)

 

Output

For each test case, output “Case #x: ans”, in which x is the case number counted from one,’ans’ is the points you can get at most

 

Sample Input

2
00?0
1 2 4 8
????
1 2 4 8

 

Sample Output

Case #1: 12
Case #2: 15
Hint
https://en.wikipedia.org/wiki/Gray_code

http://baike.baidu.com/view/358724.htm
 

 

题意：给你一串二进制代码。？既能够表示1也能够表示0。

将其转换成格雷码，每一位都有相应的数值，问将全部格雷码为1的数值相加，求最大值。

题解：首先我们要知道二进制码怎么转换为格雷码。将所需转换的数右移一位再与原数异或就可以。这里我们能够发现当前位置的取值至于下一位有关，所以我们想能够用dp解决此问题。

參考代码：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define ll long long
#define max(a,b) a>b?
a:b
using namespace std;
const int N = 200005;
const int INF = 999999999;
char s[N];
int dp[N][2], num[N];

int main() {
    int T, Case = 1;
    scanf("%d", &T);
    while (T--) {
        getchar();
        gets(s);    
        int len = strlen(s);
        for (int i = 0; i < len; i++) {
            scanf("%d", &num[i]);   
        }
        if (s[0] == '1') {
            dp[0][1] = num[0];      
            dp[0][0] = -INF;
        } else if (s[0] == '0') {
            dp[0][1] = -INF;
            dp[0][0] = 0;
        } else {
            dp[0][1] = num[0];
            dp[0][0] = 0;
        }
        for (int i = 1; i < len; i++) {
            if (s[i] == '0') {
                dp[i][0] = max(dp[i - 1][1] + num[i], dp[i - 1][0]);
                dp[i][1] = -INF;    
            } else if (s[i] == '1') {
                dp[i][1] = max(dp[i - 1][0] + num[i], dp[i - 1][1]);
                dp[i][0] = -INF;
            } else {
                dp[i][1] = max(dp[i - 1][0] + num[i], dp[i - 1][1]);
                dp[i][0] = max(dp[i - 1][1] + num[i], dp[i - 1][0]);
            }
        }
        printf("Case #%d: ", Case++);   
        printf("%d
", max(dp[len - 1][1], dp[len - 1][0]));
    }
    return 0;
}